미분법
- 도함수는 그래프 위의 한 점에서 접선의 방정식을 구하거나 함수의 최댓값과 최솟값을 구하기 위한 도구로 사용될 뿐만 아니라 확률에서도 매우 중요한 역할을 한다.
미분 계수와 도함수
- 곡선 위의 한 점에서 이 곡선에 대한 접선의 방정식을 구하기 위한 수학적 도구인 미분 계수와 도함수의 개념을 살펴보자.
평균 변화율(Average Rate of Change)
- 함수 `y = f(x)` 에 대해 다음과 같이 `x` 가 `a` 에서 `b` 까지 변할 때, `y` 의 값은 `f(a)` 에서 `f(b)` 로 변한다.
- 이때 `x` 의 변화량 `b - a` 를 `x` 의 증분(Increments)이라 하고, `Δx = b - a` 로 나타낸다.
- 그리고 `y` 의 변화량 `f(b) - f(a)` 를 `y` 의 증분이라 하고, `Δy = f(b) - f(a)` 로 나타낸다.
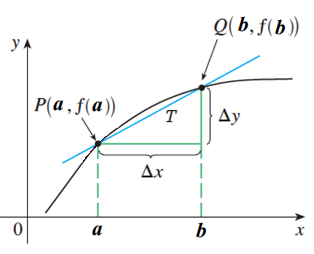
- 그리고 다음과 같이 정의되는 `x` 의 증분에 대한 `y` 의 증분의 비율을 `x` 가 `a` 에서 `b` 까지 변할 때 함수 `y = f(x)` 의 평균 변화율(Average Rate of Change)이라 한다.
$$\frac{Δy}{Δx} = \frac{f(b) - f(a)}{b - a} = \frac{f(a + Δx) - f(a)}{Δx}$$
- 그러면 평균 변화율은 그래프 위의 두점 $P(a, f(a)), \; Q(b, f(b))$ 를 지나는 직선의 기울기와 같다.
순간 변화율(Instantaneous Rate of Change)
- `b = a + Δx` 가 `a` 에 가까워진다면, 즉 `Δx → 0` 이면 다음과 같이 그래프 위의 점 `Q` 는 곡선을 따라서 점 `P` 에 가까워진다.
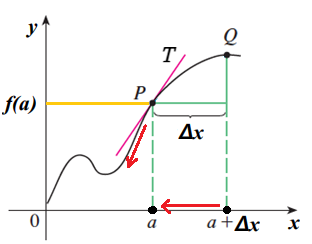
- 이 때, 다음과 같은 평균 변화율의 극한값이 존재한다면, `f(x)` 는 `x = a` 에서 미분 가능하다(Differentiable)고 한다.
$$\lim_{Δx→0} \frac{Δy}{Δx} = \lim_{Δx→0} \frac{f(a + Δx) - f(a)}{Δx}$$
- 이 극한값을 `x = a` 에서 함수 `f(x)` 의 순간 변화율(Instantaneous Rate of Change) 또는 미분 계수(Differential Coefficient)라 하고, `f'(a)` 로 나타낸다.
- 즉, `x = a` 에서 함수 `f(x)` 의 순간 변화율은 다음과 같이 정의한다.
$$f'(a) = \lim_{Δx→0} \frac{f(a + Δx) - f(a)}{Δx} = \lim_{h→0} \frac{f(a + h) - f(a)}{h} = \lim_{b→a} \frac{f(b) - f(a)}{b - a}$$
- 그리고 순간 변화율 `f'(a)` 가 존재한다면, 그래프 위의 두 점 `P` 와 `Q` 를 지나는 직선은 점 `P` 에서의 접선 `PT` 에 한없이 가까워진다.
- 따라서 함수 `y = f(x)` 의 `x = a` 에서의 미분 계수 `f'(a)` 는 점 `P(a, f(a))` 에서의 접선의 기울기이고, 이 점에서 접선의 방정식은 다음과 같다.
$$y = f'(a)(x - a) + f(a)$$
미분 가능성과 연속성
- `x = a` 에서 함수 `y = f(x)` 의 연속성과 미분 가능성에 대해 다음 성질이 성립한다.
함수 `f(x)` 가 `x = a` 에서 미분 가능하면, 함수 `f(x)` 는 `x = a` 에서 연속이다.
- 하지만, 이 성질의 역은 성립하지 않는다.
- `f(x)` 가 `x = a` 에서 연속이면, 함수 `f(x)` 가 `x = a` 에서 미분 가능하다. (X)
- 반례) `f(x) = |x|` 는 `x = 0` 에서 연속이지만, 미분 가능하지 않다. (뾰족 함수)
- `f(x)` 가 `x = a` 에서 연속이면, 함수 `f(x)` 가 `x = a` 에서 미분 가능하다. (X)
증명
`x ≠ a` 이면, `f(x) = \frac{f(x) - f(a)}{x - a} × (x - a) + f(a)`
$\Rightarrow$ $\lim_{x→a}\limits f(x) = \lim_{x→a}\limits \left( \frac{f(x) - f(a)}{x - a} × (x - a) + f(a) \right) = \lim_{x→a}\limits \frac{f(x) - f(a)}{x - a} × \lim_{x→a}\limits (x - a) + \lim_{x→a}\limits f(a) = f'(a) × 0 + f(a) = f(a)$
따라서 `f(x)` 가 `x = a` 에서 연속이다.
미분이 불가능한 경우
- 보통 함수의 모양이 다음과 같을 경우 미분이 불가능하다.
① 그래프가 도중에 끊어질 경우 (불연속)
② 그래프가 뾰족할 경우
도함수(Derivative)
- 함수 `y = f(x)` 의 정의역 안의 미분 가능한 점 `x` 에 대해 그 점에서의 미분 계수 `f'(x)` 를 대응시키는 새로운 함수 $f' \; : \; x \; → \; f'(x)$ 를 다음과 같이 정의할 수 있다.
$$f'(x) = \lim_{h→0}\frac{f(x + h) - f(x)}{h}$$
- 이와 같이 유도된 함수 `f'(x)` 를 함수 `f(x)` 의 도함수(Derivative)라 하고, 다음과 같이 나타낸다.
$$y', f'(x), \frac{dy}{dx}, \frac{df}{dx}, \frac{d}{dx}f(x), Df(x)$$
- 그리고 함수 `y = f(x)` 에 대한 도함수 `f'(x)` 를 구하는 것을 미분한다(Differentiate)고 하고, 도함수를 구하는 방법을 미분법(Differentiation)이라 한다.
미분법(Differentiation)
- 함수의 도함수를 구하기 위해 매번 도함수의 정의를 사용하는 것은 매우 불편하다.
- 따라서 도함수를 구하기 위한 다양한 종류의 미분법과 확률에서 나타나는 특수한 함수들의 도함수를 살펴보자.
`x^{α}` 의 미분법
- 양의 정수 `m` 과 `n(≠0)` 에 대해 `frac{1}{x^{n}} = x^{-n}`, $\sqrt [n] {x^{m}} = x^{m/n}$ 으로 나타낸다.
- 이와 같이 지수가 음의 정수와 유리수인 경우의 도함수를 다음과 같이 양의 지수를 갖는 경우와 동일한 방법으로 구할 수 있다.
- 이 방법은 지수가 무리수인 경우에도 적용된다.
임의의 실수 `α` 에 대해 $(x^{α})' = αx^{α - 1}$ 이다.
- 특히, `α = 0` 이면, `x^{0} = 1` 이고, 따라서 $(1)' = (x^{0})' = 0(x^{-1}) = 0$ 이다.
예제 : 다음 함수의 도함수를 구하라.
(a) `x^{2}`
(b) `\frac{1}{x^{2}}`
(c) `x^{\sqrt{2}}`
(d) $\sqrt[3]{x^{2}}$
(a) $(x^{2})' = 2x^{2-1} = 2x$
(b) $(\frac{1}{x^{2}})' = (x^{-2})' = (-2)x^{-2-1} = (-2)x^{-3} = -\frac{2}{x^{3}}$
(c) $(x^{\sqrt{2}})' = \sqrt{2}x^{\sqrt{2}-1}$
(d) $(\sqrt[3]{x^{2}})' = (x^{2/3})' = \frac{2}{3}x^{(2/3) - 1} = \frac{2}{3}x^{-1/3} = \frac{2}{3\sqrt[3]{x}}$
미분법의 기본 공식
- 거듭 제곱 함수의 모양으로 주어진 함수들은 가감 승제에 의한 새로운 함수의 도함수를 구할 수 있는데, 이때 미분법의 기본 공식을 이용한다.
함수 `f(x)` 와 `g(x)` 가 미분 가능하면 다음이 성립한다.
(1) $[kf(x)]' = kf'(x),$ (단, `k` 는 상수)
(2) $[f(x)±g(x)]' = f'(x) ± g'(x)$ (복부호 동순)
(3) $[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)$
(4) $\left [\frac{1}{g(x)} \right]' = - \frac{g'(x)}{[g(x)]^{2}}$
(5) $\left [\frac{f(x)}{g(x)} \right]' = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^{2}}$
- 미분법의 기본 공식 정리 (3)을 세 함수 `f(x)`, `g(x)`, `h(x)` 에 적용하면 다음을 얻을 수 있다.
$$[f(x)g(x)h(x)]' = f'(x)g(x)h(x) + f(x)g'(x)h(x) + f(x)g(x)h'(x)$$
예제 : 다음 함수의 도함수를 구하라.
(a) `4x^{2}`
(b) `\frac{1}{\sqrt{x}}`
(c) `(x + 2)^{2}`
(d) $\frac{2x + 1}{x^{2}-x+1}$
(a)
$(4x^{2})' = 4(x^{2})' = 4(2x) = 8x$
(b)
`f(x) = \sqrt{x}` 라 하면, `f(x) = x^{1/2}` 이므로, `f'(x) = \frac{1}{2}x^{(1/2)-1} = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}` 이다.
따라서 구하고자 하는 도함수는 다음과 같다.
$\left ( \frac{1}{\sqrt{x}} \right )' = - \frac{(\sqrt{x})'}{(\sqrt{x})^{2}} = -\frac{1}{x} · \frac{1}{2\sqrt{x}} = - \frac{1}{2x\sqrt{x}}$
(c)
$\{(x+2)^{2}\}' = (x^{2}+4x+4)' = (x^{2})' + (4x)' + (4)' = 2x + 4(x)' + 4(0) = 2x + 4$
(d)
`f(x) = 2x + 1`, `g(x) = x^{2} - x + 1` 이라 하면 `f'(x)` 와 `g'(x)` 는 각각 다음과 같다.
$f'(x) = (2x + 1)' = (2x)' + (1)' = 2$
$g'(x) = (x^{2} -x + 1)' = (x^{2})' + (-x)' + (1)' = 2x - 1$
따라서 구하고자 하는 도함수는 다음과 같다.
$\left ( \frac{2x^{2}+2x-3}{x^{2}-x+1} \right )' = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^{2}} = \frac{2·(x^{2}-x+1) - (2x+1)(2x -1)}{(x^{2}-x+1)^{2}} = - \frac{2x^{2}+2x-3}{(x^{2}-x+1)^{2}}$
합성 함수의 미분법
- 미분 가능한 두 함수 `f(x) = x^{5}` 과 `g(x) = x^{2} - 5x + 6` 의 합성 함수 `f(g(x)) = (x^{2} - 5x + 6)^{5}` 의 도함수를 구한다고 하자.
- 이를 위해 미분법의 기본 공식을 이용한다면, 이 합성 함수를 전개하여 각각의 항들을 미분하고, 이를 다시 정리해야 하는 번거로움이 있다.
- 이와 같은 합성 함수에 대해 쉽게 미분하는 방법으로 연쇄 법칙(Chain Rule)이 있다.
연쇄 법칙(Chain Rule)
- 두 함수 `y = f(u)` 와 `u = g(x)` 가 각각 미분 가능하면 합성 함수 `y = f(g(x))` 도 미분 가능하고, 다음이 성립한다.
$$\frac{dy}{dx} = \frac{dy}{du} · \frac{du}{dy} = f'(g(x))g'(x)$$
- 또한 미분 가능한 함수 `f(x)` 에 대해 `x^{α}` 의 미분법과 연쇄 법칙을 이용하면 다음을 얻을 수 있다.
$$[\{f(x)\}^{α}]' = α\{f(x)\}^{α - 1}f'(x)$$
예제 : 다음 함수의 도함수를 구하여라.
(a) $(x^{2} - 5x + 6)^{5}$
(b) $(\frac{2x + 1}{x^{2}-x+1})^{2}$
(a)
$y = (x^{2} - 5x + 6)^{5}, \; u = x^{2} - 5x + 6$ 이라 하면, `y = u^{5}` 이므로 다음을 얻는다.
$\frac{dy}{du} = 5u^{4}, \; \frac{du}{dx} = 2x - 5$
따라서 구하고자 하는 도함수는 다음과 같다.
$\frac{dy}{dx} = \frac{dy}{du} · \frac{du}{dx} = (5u^{4})(2x - 5) = 5(2x - 5)(x^{2} - 5x + 6)^{4}$
(b)
$y = \left( \frac{2x + 1}{x^{2} - x + 1} \right)^{2}, \; u = \frac{2x + 1}{x^{2} -x + 1}$ 이라 하면, `y = u^{2}` 이므로 다음을 얻는다.
$\frac{dy}{du} = (u^{2})' = 2u, \; \frac{du}{dx} = - \frac{2x^{2} + 2x - 3}{(x^{2} -x + 1)^{2}}$
따라서 구하고자 하는 도함수는 다음과 같다.
$\frac{dy}{dx} = \frac{dy}{du} · \frac{du}{dx} = (2u) \left ( - \frac{2x^{2}+2x-3}{(x^{2}-x+1)^{2}} \right ) = - \frac{2(2x+1)(2x^{2}+2x-3)}{(x^{2}-x+1)^{3}}$
초월 함수의 미분법
- 가장 기본적인 초월 함수인 지수 함수, 로그 함수 그리고 삼각 함수의 미분법과 이 함수들의 합성 함수에 대한 도함수를 쉽게 구할 수 있다.
지수 함수와 로그 함수의 미분법
(1) 함수 `y = e^{x}` 은 모든 실수에서 미분 가능하며, `(e^{x})' = e^{x}` 이다.
(2) 함수 `y = \ln x` 는 `x > 0` 에서 미분 가능하며, `(\ln x)' = \frac{1}{x}` 이다.
- 연쇄 법칙을 적용하면 미분 가능한 함수 `f(x)` 에 대해 다음을 얻을 수 있다.
$$\{e^{f(x)}\}' = f'(x)e^{f(x)}, \; \{\ln f(x) \}' = \frac{f'(x)}{f(x)}$$
초월 함수(Transcendental Function)
- 다항식의 근으로 정의할 수 없는 함수
- 초월 함수는 유한한 대수 연산(덧셈, 곱셈, 거듭제곱)으로 표현할 수 없기 때문에 대수학을 '초월'하는 함수이다.
- 다음의 함수들은 초월 함수에 해당한다.
- 자세한 내용은 이곳을 참고한다.
- $f_{1}(x) = x^{π}$
- $f_{2}(x) = c^{x}$ (`c` 를 자연 로그의 밑인 `e` 로 둘 경우, `e^{x}` 가 초월 함수라는 것을 얻을 수 있다.)
- $f_{3}(x) = x^{x}$
- $f_{4}(x) = x^{\frac{1}{x}}$
- $f_{5}(x) = \log_{c} x$ (`c` 를 `e` 로 둘 경우, 자연 로그인 $\log_{e} x = \ln x$ 를 얻을 수 있다.)
- $f_{6}(x) = \sin x$
예제 : 다음 함수의 도함수를 구하라.
(a) $x^{2}e^{x}$
(b) $e^{2x^{2}+x}$
(c) $x^{2}\ln x$
(d) $\ln (x^{2} + 2x + 3)$
(a) $x(x+2)e^{x}$
(b) $(4x + 1)e^{2x^{2}+x}$
(c) $x(1 + 2\ln x)$
(d) $\frac{2(x+1)}{x^{2}+2x+3}$
삼각 함수의 미분법
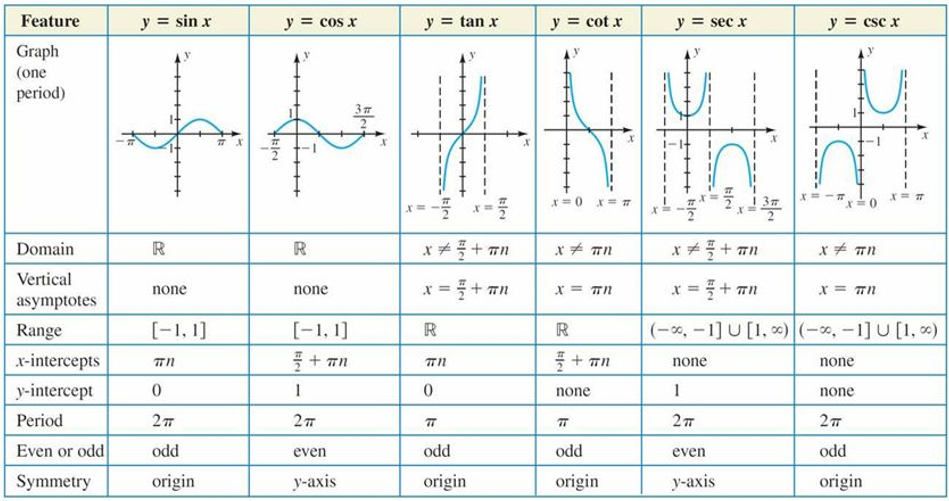
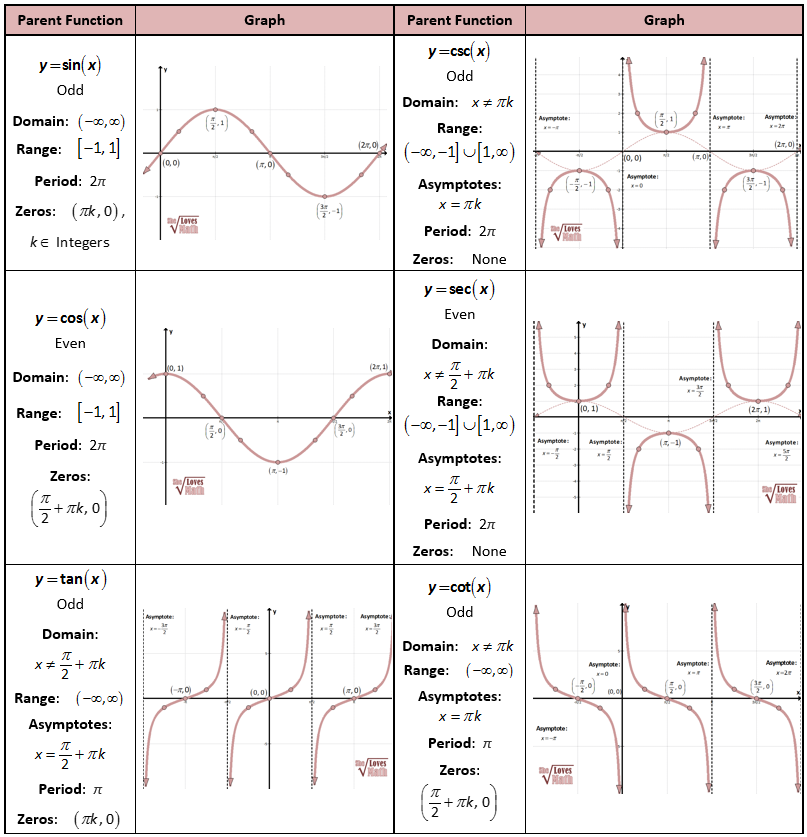
(1) $(\sin x)' = \cos x$
(2) $(\cos x)' = - \sin x$
(3) $(\tan x)' = \sec^{2} x$
(4) $(\sec x)' = \sec x \tan x$
(5) $(cosec\;x)' = -cosec\;x \cot x$
(6) $(\cot x)' = - cosec^{2}\;x$
삼각 함수(Trigonometric Functions; Angle Function; Circular Function; Oniometric Function)
- 각의 크기를 삼각비로 나타내는 함수
- 자세한 내용은 이곳을 참고한다.
- 삼각 함수의 그래프
예제 : 다음 함수의 도함수를 구하라.
(a) $\sin (2x + 1)$
(b) $\cos^{2} x$
(c) $\tan^{2} (2x - 1)$
(a) $2\cos (2x + 1)$
(b) $-2\sin x \cos x$
(c) $\frac{4\sin (2x - 1)}{\cos^{3}(2x-1)}$
고계 도함수(Higher Derivative)
- 함수 `y = f(x)` 가 미분 가능하면, 도함수 `f'(x)` 의 도함수를 함수 `y = f(x)` 의 2계 도함수라고 하고, 다음과 같이 나타낸다.
$$y'', \; f''(x), \; \frac{d^{2}y}{dx^{2}}, \; \frac{d^{2}}{dx^{2}}f(x), \; D^{2}f(x)$$
- 또한 2계 도함수 `f''(x)` 가 미분 가능할 때, `f''(x)` 의 도함수를 함수 `y = f(x)` 의 3계 도함수라고 하고, 다음과 같이 나타낸다.
$$y''', \; f'''(x), \; \frac{d^{3}y}{dx^{3}}, \; \frac{d^{3}}{dx^{3}}f(x), \; D^{3}f(x)$$
- 일반적으로 함수 `y = f(x)` 를 연속적으로 `n` 번 미분하여 얻은 함수를 `y = f(x)` 의 `n` 계 도함수라 하고, `n ≥ 4` 인 경우에 다음과 같이 나타낸다.
- 이러한 도함수들을 함수 `y = f(x)` 의 고계 도함수(Higher Derivative)라 한다.
$$y^{(n)}, \; f^{(n)}(x), \; \frac{d^{n}y}{dx^{n}}, \; \frac{d^{n}}{dx^{n}}f(x), \; D^{n}f(x)$$
- 고계 도함수를 다음과 같이 일반화할 수도 있다.
$$y^{(n)} = (y^{(n - 1)})' = f^{(n)} = \frac{d^{n}y}{dx^{n}}$$
예제 : 자연수 `n` 에 대하여 함수 `y = x^{n}` 의 `k` 계 도함수 `y^{(k)}` 를 구하여라.
pf)
$y = x^{n}$
$y' = nx^{n-1}$
$y'' = n(n-1)x^{n-2}$
$y''' = n(n-1)(n-2)x^{n-3}$
…
이므로,
$y^{(n)} = n(n-1)(n-2) \cdots 3 · 2 · 1 · x^{n-n} = n(n-1)(n-2)\cdots 3 · 2 · 1 = n!$ 이다.
따라서 임의의 자연수 `k` 에 대해 `f(x) = x^{n}` 의 `k` 계 도함수는 다음과 같다.
$y^{(k)} = \cases{ n(n-1)\cdots (n-k+1)x^{n-k} & (k < n) \cr n! & (k = n) \cr 0 & (k > n) }$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
|---|---|
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 적분법 (1) | 2022.10.03 |
| [확률과 통계] 함수의 극한과 연속 (0) | 2022.09.27 |
| [확률과 통계] 경우의 수 (0) | 2022.09.21 |
| [확률과 통계] 함수 (0) | 2022.09.20 |
| [확률과 통계] 집합 (1) | 2022.09.15 |