적분법
- 적분은 미분의 역산으로, 연속 확률 변수에 대한 확률을 계산할 때 사용한다.
- 또한, 연속 확률 변수의 확률 밀도 함수를 적분하여 분포 함수를 얻으므로, 적분의 개념은 확률에서 매우 중요하다.
부정 적분(Indefinite Integral)
- 연속 함수 `f(x)` 가 주어졌을 때, 이 함수를 도함수로 가지는 함수 `F(x)` 가 존재하면, 함수 `F(x)` 를 `f(x)` 의 부정 적분(Indefinite Integral) 또는 원시 함수(Primitive Function)라 한다.
- 원시 함수와 도함수 사이에는 다음 관계가 성립한다.
$$F'(x) = f(x)$$
- 이때 `F(x)` 를 다음과 같이 나타내며, 기호 $\int$ 를 적분 기호(Symbol of Integral), `f(x)` 를 피 적분 함수(Integrand), 그리고 `x` 를 적분 변수(Variable of Integrand)라 한다. 여기서 `C` 는 상수이다.
$$F(x) = \int f(x)dx + C$$
- 한편, 함수 `f(x)` 의 특정한 부정 적분을 `F(x)` 라 하면, 다음이 성립한다.
$$\{F(x) + C\}' = F'(x) + C' = F'(x) = f(x)$$
- 그러므로 함수 `F(x) + C` 도 역시 함수 `f(x)` 의 부정 적분이다.
- 따라서 함수 `f(x)` 의 부정 적분을 `F(x)` 와 `G(x)` 라 하면 다음 관계가 성립한다.
- 이때 상수 `C` 를 적분 상수(Integration Constant)라 한다.
$$F(x) - G(x) = C$$
- 일반적으로 함수 `f(x)` 의 부정 적분은 적분 상수 `C` 를 이용하여 다음과 같이 나타낸다.
$$\int f(x)dx = F(x) + C$$
예제 : 다음 부정 적분을 구하라
(a) $\displaystyle \int 4x^{3} dx$
(b) $\displaystyle \int \frac{1}{x} dx$
(a)
$(x^{4})' = 4x^{3}$ 이므로, $\int 4x^{3} dx = x^{4} + C$
(b)
$(\ln x)' = \frac{1}{x}$ 이므로, $\int \frac{1}{x} dx = \ln |x| + C$
$\int \frac{1}{x} dx = \ln |x|$ ?
- $\displaystyle \int \frac{1}{x} dx$ = ln |x| 임에 주의한다.
- $∵ [\ln(-x)]' = \frac{1}{-x} × (-1) = \frac{1}{x}$
적분법(Integration)
- 임의의 상수 `a`, `b` 와 미분 가능한 두 함수 `F(x)`, `G(x)` 에 대해 다음 사실을 알고 있다.
$$\{aF(x) + bG(x)\}' = aF'(x) + bG'(x)$$
- 그러면 적분은 미분의 역산이므로 다음이 성립한다.
$$\int [aF'(x) + bG'(x)] dx = aF(x) + bG(x)$$
- 그러므로 두 함수 `F(x)` 와 `G(x)` 를 각각 `f(x)` 와 `g(x)` 의 원시 함수라고 하면, `F'(x) = f(x)`, `G'(x) = g(x)` 이고, 다음이 성립한다.
$$F(x) = \int f(x)dx, \; G(x) = \int g(x)dx$$
- 따라서 적분에 대한 다음의 기본 공식을 얻는다.
적분의 기본 공식
- `f(x)` 와 `g(x)` 가 적분 가능하다면, 다음이 성립한다.
$$\int [af(x) + bg(x)] dx = a \int f(x) dx + b \int g(x) dx$$
초월 함수의 적분법
기본 함수의 적분법
- 적분은 미분의 역산이므로, 미분법의 역산에 의해 기본적인 적분 공식을 얻는다.
(1) $\displaystyle \int x^{α} dx = \frac{x^{α + 1}}{α + 1} + C$ (단, `α ≠ 1` 인 실수)
(2) $\displaystyle \int \frac{1}{x} dx = \ln |x| + C$
(3) $\displaystyle \int e^{x} dx = e^{x} + C$
삼각 함수의 적분법
- 적분은 미분의 역산이므로, 미분법의 역산에 의해 삼각 함수의 적분 공식을 얻는다.
(1) $\displaystyle \int \sin x dx = - \cos x + C$
(2) $\displaystyle \int \cos x dx = \sin x + C$
(3) $\displaystyle \int \sec^{2} x = \tan x + C$
(4) $\displaystyle \int cosec^{2} \; xdx = - \cot x + C$
(5) $\displaystyle \int \sec x \tan x dx = \sec x + C$
(6) $\displaystyle \int cosec \; x \cot x dx = - cosec \; x + C$
예제 : 다음 부정 적분을 구하라.
(a) $\displaystyle \int (2x + 3)dx$
(b) $\displaystyle \int \left(x + \frac{1}{x} \right)dx$
(a)
$\int (2x + 3)dx = 2 \int xdx + 3 \int 1 dx = 2 \left ( \frac{1}{2} x^{2} \right) + 3(x) + C = x^{2} + 3x + C$
(b)
$\int \left (x + \frac{1}{x} \right) dx = \int x dx + \int \frac{1}{x} dx = \frac{1}{2}x^{2} + ln |x| + C$
치환 적분법(Integration by Substitution)
- 함수 `F(u)` 가 함수 `f(u)` 의 원시 함수이고, `u = g(x)` 가 미분 가능하면, 합성 함수의 미분법에 의해 `y = F(g(x))` 의 도함수는 다음과 같다.
$$\frac{d}{dx}F(g(x)) = \frac{dy}{du} · \frac{du}{dx} = f(g(x))g'(x)$$
- 따라서 `F(g(x))` 는 `f(g(x))g'(x)` 의 원시 함수이고, 다음이 성립한다.
$$\int f(g(x))g'(x)dx = F(g(x)) + C$$
- 그러므로 피 적분 함수가 `f(g(x))g'(x)` 일 때, `u = g(x)` 로 치환하며 `g'(x)dx = du` 이다.
- 그러면 피 적분 함수의 적분 결과는 다음과 같으며, 이를 치환 적분법(Integration by Substitution)이라 한다.
$$\int f(g(x))g'(x) dx = \int f(u)du = F(u) + C = F(g(x)) + C$$
- 그러면 치환 적분법을 이용하여 다음 적분 공식을 얻을 수 있다.
치환 적분 공식
(1) $\displaystyle \int [f(x)]^{n}f'(x)dx = \frac{1}{n + 1}[f(x)]^{n+1} + C$ (단, $n ≠ -1$)
(2) $\displaystyle \int \frac{f'(x)}{f(x)} dx = \ln |f(x)| + C$
예제 : 다음 부정 적분을 구하라.
(a) $\displaystyle \int 2(2x + 3)^{5} dx$
(b) $\displaystyle \int \frac{2x + 1}{x^{2} + x} dx$
(c) $\displaystyle \int \tan x dx$
(d) $\displaystyle \int \frac{\ln x}{x} dx$
(a)
`u = 2x + 3` 이라 하면 `\frac{du}{dx} = 2` 이므로 `2dx = du` 이고, 다음 부정 적분을 얻는다.
$\displaystyle \int 2(2x + 3)^{5}dx = \int(2x + 3)^{5} · 2dx = \int u^{5}du = \frac{1}{6}u^{6} + C = \frac{1}{6}(2x + 3)^{6} + C$
(b)
`f(x) = x^{2} + x` 라 하면, `f'(x) = 2x + 1` 이므로 $\displaystyle \int \frac{2x + 1}{x^{2} + x} dx = \ln |x^{2} + x| + C$ 이다.
(c)
$u = \cos x \Rightarrow du = - \sin x dx$
$\displaystyle \int \tan x dx = \int \frac{\sin x}{\cos x} dx = \int \frac{-1}{u}du = -\ln |u| + C = - \ln | \cos x | + C$
(d)
$\displaystyle u = \ln x \Rightarrow du = \frac{1}{x} dx$
$\displaystyle \int \frac{\ln x}{x} dx = \int udu = \frac{1}{2}u^{2} + C = \frac{1}{2}(\ln x)^{2} + C$
부분 적분법(Integration by Parts)
- 두 함수 `u = f(x), \; v = g(x)` 의 곱에 대한 미분법은 다음과 같다.
$$\{ f(x)g(x) \}' = f'(x)g(x) + f(x)g'(x)$$
- 따라서 양분을 적분하면 다음을 얻는다.
$$\int [f'(x)g(x) + f(x)g'(x)]dx = f(x)g(x)$$
- 그러면 피 적분 함수가 `f(x)g'(x)` 인 경우에 다음과 같이 부정 적분을 구할 수 있다.
- 보통, 간단하게 미분되는 것을 `g(x)` 로 선정한다.
$$\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx$$
- 이와 같은 방법에 의해 부정 적분을 구하는 방법을 부분 적분법(Integration by Parts)이라 하며, 피 적분 함수가 다항식과 초월 함수의 곱으로 구성된 경우에 사용한다.
예제 : 다음 부정 적분을 구하라.
(a) $\displaystyle \int xe^{x} dx$
(b) $\displaystyle \int x \cos x dx$
(a)
$f(x) = x, \; g'(x) = e^{x}$ 이라 하면, $f'(x) = 1, \; g(x) = e^{x}$ 이므로 다음 부정 적분을 얻는다.
$\displaystyle \int xe^{x}dx = xe^{x} - \int 1 · e^{x}dx = xe^{x} - e^{x} + C = (x - 1)e^{x} + C$
(b)
$f(x) = x, \; g'(x) = \cos x$ 라 하면, $f'(x) = 1, \; g(x) = \sin x$ 이므로 다음 부정 적분을 얻는다.
$\displaystyle x \cos x dx = x \sin x - \int 1 · \sin x dx = x \sin x - (- \cos x) + C = x \sin x + \cos x + C$
정적분(Definite Integral)과 기본 정리
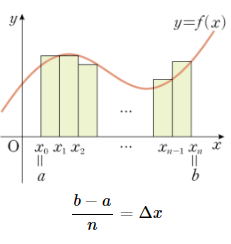
- 함수 `y = f(x)` 가 폐구간 `[a, b]` 에서 연속이고, 이 구간에서 `f(x) ≥ 0` 이라고 하자.
- 그리고 함수 `y = f(x)` 와 직선 $x = a, \; x = b$ 그리고 `x` 축으로 둘러사인 부분의 넓이를 `I` 라고 하자.
- 이제 폐구간 `[a, b]` 를 `n` 등분하여 양 끝점과 각 분할된 점의 `x` 좌표를 다음과 같이 나타낸다.
$$a = x_{0} < x_{1} < x_{2} < \cdots < x_{n-1} < x_{n} = b$$
- 그리고 소구간의 길이를 $\displaystyle \frac{b-a}{n} = Δx$ 라 하면, 각 분할 점 `x_{k}` 는 다음과 같다.
$$x_{k} = a + kΔx = a + \frac{k}{n}(b - a)$$
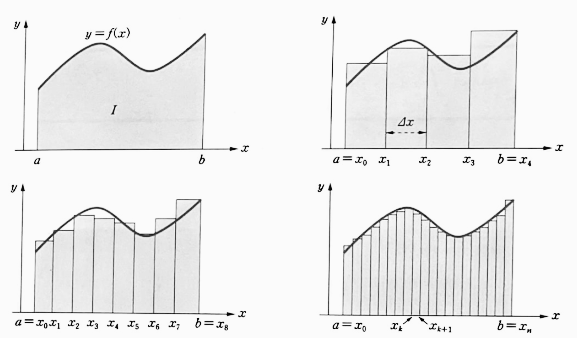
- 이 때, `n` 의 사각형의 넓이의 합을 `S_{n}` 이라 하면, `n` 이 커질수록 `S_{n}` 의 넓이는 `I` 에 가까워지는 것을 알 수 있다.
- 실제로 `n` 이 커질수록 사각형의 넓이의 합 `S_{n}` 은 반드시 수렴하며, $\displaystyle \lim_{n→∞} S_{n} = I$ 이다. 즉, 다음이 성립한다.
$$ \lim_{n→∞} S_{n} = \lim_{n→∞} \sum_{k=1}^{n}f(x_{k})Δx = I$$
- 이 극한값 `I` 를 폐구간 `[a, b]` 에서 함수 `f(x)` 의 정적분(Definite Integral)이라 하고, 다음과 같이 나타낸다.
$$I = \lim_{n→∞} S_{n} = \lim_{n→∞} \sum_{k=1}^{n}f(x_{k})Δx = \int_{a}^{b} f(x)dx$$
- 극한값 `I` 가 존재할 때 함수 `f(x)` 는 폐구간 `[a, b]` 에서 적분 가능(Integrable)하다고 하고, `a` 를 적분 하한(Lower Limit of Integration), `b` 를 적분 상한(Upper Limit of Integration)이라 한다.
- 그러면 폐구간에서 연속인 함수는 반드시 적분 가능하다.
- 따라서 폐구간 `[a, b]` 에서 연속이고, 이 구간에서 `f(x) ≥ 0` 인 함수 `y = f(x)` 의 정적분은 곡선 `y = f(x)` 와 `x = a, x = b` 그리고 `x` 축으로 둘러싸인 부분의 넓이와 같다.
- 이러한 사실은 연속 확률 변수에 대한 확률을 계산할 때 응용된다.
예제 : 정적분의 정의를 이용하여 $\displaystyle \int _{0}^{b} x^{2} dx$ 를 구하라. (단, `b > 0` 이다.)
Pf)
폐구간 `[0, b]` 를 `n` 등분하면 다음 그림과 같이 각 소구간의 오른쪽 끝점은 $x_{k} = \frac{kb}{n}$ 이다.
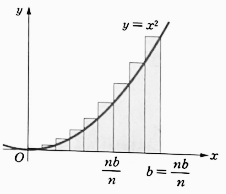
그러면 모든 소구간의 길이는 `Δx = \frac{b}{n}` 이고, 오른쪽 끝점에서의 함숫값은 $f(x_{k}) = \left ( \frac{kb}{n} \right )^{2}$ 이다. 따라서 구하고자 하는 정적분은 다음과 같다.
$\displaystyle \int^{b}_{0}x^{2}dx = \lim_{n→∞} \sum^{n}_{k=1} f(x_{k})Δx = \lim_{n→∞} \sum^{n}_{k=1} (\frac{kb}{n})^{2}(\frac{b}{n}) = \lim_{n→∞} \frac{b^{3}}{n^{3}}\sum^{n}_{k=1}k^{2} = \lim_{n→∞} \frac{b^{3}}{n^{3}} · \frac{n(n+1)(2n+1)}{6} = \frac{b^{3}}{3}$
정적분의 기본 정리
- 한편, 함수 `f(x)` 의 한 부정 적분 `F(x)` 를 알고 있다면, 폐구간 `[a, b]` 에서 `f(x)` 의 정적분을 다음과 같이 쉽게 구할 수 있다.
`f(x)` 가 연속이면 다음이 성립한다.
(1) $\displaystyle \frac{d}{dx} \left( \int_{a}^{x} f(t)dt \right) = f(x)$
`f(x)` 가 폐구간 `[a, b]` 에서 연속이고, `F'(x) = f(x)` 이면 다음이 성립한다.
(2) $\displaystyle \int_{a}^{b} f(x)dx = F(b) - F(a) (= F(x) |^{b}_{a})$
증명
$\displaystyle G(x) = \int_{a}^{x} f(t)dt$ 라고 하자.
$G'(x) = f(x) = F'(x) \Rightarrow G(x) = F(x) + C \; (C ∈ R)$
$G(a) = 0 \Rightarrow F(a) + C = 0 \Rightarrow C = -F(a)$
∴ $\displaystyle \int_{a}^{b} f(x)dx = G(b) = F(b) - F(a) $
예제 : 정적분 $\displaystyle \int_{0}^{2}x^{2}dx$ 를 구하여라.
Pf)
우선, 대표적인 원시 함수를 구하면 $\displaystyle F(x) = \int x^{2}dx = \frac{1}{3}x^{3}$ 이다.
따라서 구하고자 하는 정적분은 다음과 같다.
$\displaystyle \int_{0}^{2}x^{2}dx = \left[ \frac{1}{3}x^{3} \right]^{2}_{0} = \frac{8}{3} - \frac{0}{3} = \frac{8}{3}$
(위의 첫 번째 예제에서 `b = 2` 인 경우와 동일하다.)
정적분의 성질
- 한편, 정적분은 적분법에서 살펴본 부정 적분의 성질을 갖는다.
(1) $\displaystyle \int_{a}^{b} [αf(x) + βg(x)]dx = α \int_{a}^{b}f(x)dx + β \int_{a}^{b} g(x)dx$
(2) $\displaystyle \int_{a}^{b} f(x)dx = \int_{a}^{c} f(x)dx + \int_{c}^{b} f(x)dx$
(3) $\displaystyle \int_{a}^{b} f(x)dx = - \int_{a}^{b} f(x)dx$
(4) $\displaystyle f(x) ≤ g(x) \Rightarrow \int_{a}^{b} f(x)dx ≤ \int_{a}^{b} g(x)dx$
(5) $\displaystyle \int_{a}^{b} f(g(x))g'(x)dx = \int_{α}^{β}f(u)du = [F(u)]^{β}_{α}$ (단, $α = g(a), \; β = g(b)$)
(6) $\displaystyle \int_{a}^{b} f(x)g'(x) dx = [f(x)g(x)]^{b}_{a} - \int_{a}^{b} f'(x)g(x) dx$
예제 : 다음 정적분을 구하라.
(a) $\displaystyle \int_{0}^{2} xe^{x}dx$
(b) $\displaystyle \int_{0}^{2} xe^{x^{2}}dx$
(c) $\displaystyle \int_{0}^{π/2} x \cos x dx$
(a)
$f(x) = x, \; g'(x) = e^{x}$ 이라 하면, $f'(x) = 1, \; g(x) = e^{x}$ 이므로 다음 정적분을 얻는다.
$\displaystyle \int_{0}^{2} xe^{x}dx = [xe^{x}]^{2}_{0} - \int_{0}^{2}1 · e^{x}dx = (2e^{2} - 0) - [e^{x}]^{2}_{0} = 2e^{2} - (e^{2} - 1) = 1 + e^{2}$
(b)
치환 적분을 이용하여 문제를 해결할 수 있다.
$u = x^{2}$ 이라고 하면, $du = 2xdx$ 이다.
$x = 0 \Rightarrow u = 0, \; x = 2 \Rightarrow u = 4$ 이므로, $\displaystyle \int_{0}^{2} xe^{x^{2}}dx = \int_{0}^{4}\frac{1}{2}e^{u}du = \frac{1}{2} \int_{0}^{4}e^{u}du = \frac{1}{2}[e^{u}]^{4}_{0} = \frac{1}{2}(e^{4}-1)$
(c)
부분 적분을 이용하여 문제를 해결할 수 있다.
$x = v, \; \cos x = u'$ 라고 하면, $v' = 1, u = \sin x$ 이다.
$\displaystyle \int_{0}^{π/2} x \cos x dx = [x \sin x]^{π/2}_{0} - \int_{0}^{π/2} \sin x dx = \frac{π}{2}(1 - 0) + [\cos x]_{0}^{π/2} = \frac{π}{2} + (0 - 1) = \frac{π}{2} - 1$
이상 적분(Improper Integral)
- 정적분을 정의하기 위한 조건은 적분 구간이 폐구간 `[a, b]` 이고, 이 구간에서 함수 `y = f(x)` 가 연속이어야 한다.
- 하지만, 이와 다르게 적분 구간이 무한인 경우의 정적분을 이상 적분(Improper Integral)이라 한다.
무한 구간이 $[a, \; ∞)$ 또는 $(-∞, \; a]$ 인 경우
- 무한 구간 $[a, \; ∞)$ 에서 연속 함수 `f(x)` 의 정적분은 다음과 같이 정의한다.
$$\int_{a}^{∞} f(x)dx = \lim_{M→∞} \int_{a}^{M} f(x) dx$$
- 그리고 무한 구간 $(-∞, \; a]$ 에서 연속 함수 `f(x)` 의 정적분은 다음과 같이 정의한다.
$$\int_{-∞}^{a} f(x)dx = \lim_{M→-∞} \int_{M}^{a} f(x) dx$$
- 이 때, 극한값이 존재하면 이상 적분 $\displaystyle \int_{a}^{∞} f(x)dx$ 와 $\displaystyle \int_{-∞}^{a} f(x)dx$ 는 수렴 한다(Convergent)고 하고, 수렴하지 않는 경우에는 이상 적분이 발산 한다(Divergent)고 한다.
무한 구간이 $(-∞, \; ∞)$ 인 경우
- 함수 `f(x)` 가 모든 실수 범위에서 연속이라 하자.
- 이 때, 임의의 실수 `a` 에 대해 $\displaystyle \int_{-∞}^{a} f(x)dx$ 와 $\displaystyle \int_{a}^{∞} f(x)dx$ 가 존재할 때, 적분 구간 $(-∞, \; ∞)$ 에서 이상 적분은 다음과 같이 정의한다.
$$\int_{-∞}^{∞} f(x)dx = \int_{-∞}^{a} f(x)dx + \int_{a}^{∞} f(x)dx$$
- 그리고 무한 구간 $(-∞, \; ∞)$ 에서 연속 함수 `f(x)` 의 정적분은 다음과 같이 정의한다.
$$\int_{-∞}^{∞} f(x)dx = \int_{-∞}^{a} f(x)dx + \int_{a}^{∞} f(x)dx = \lim_{M→-∞} \int_{M}^{a} f(x) dx + \lim_{M→∞} \int_{a}^{M} f(x) dx$$
- 특히 무한 구간 `(-∞, \; ∞)` 에서 연속이고 음이 아닌 함수 `f(x)` 가 다음을 만족한다면, 이 함수 `f(x)` 를 확률 밀도 함수(Probability Density Function)라고 한다.
$$\int_{-∞}^{∞} f(x)dx = 1$$
예제 : 다음 이상 적분을 구하라.
(a) $\displaystyle \int_{0}^{∞}e^{-2x}dx$
(b) $\displaystyle \int_{-2}^{2}\frac{1}{x}dx$
(a)
$\displaystyle \int_{0}^{∞}e^{-2x}dx = \lim_{b→∞} \int_{0}^{b}e^{-2x}dx = \lim_{b→∞}(-\frac{1}{2}e^{-2x})|^{b}_{0} = \frac{1}{2} \lim_{b→∞} (1 - e^{-2b}) = \frac{1}{2}$
(b)
$\displaystyle \int_{-2}^{2}\frac{1}{x}dx = \int_{-2}^{0}\frac{1}{x}dx + \int_{0}^{2}\frac{1}{x}dx = \lim_{M→0-} \int_{-2}^{M} \frac{1}{x} dx + \lim_{m→0+} \int_{M}^{2}\frac{1}{x}dx$
(이 경우에는 무한대(`∞`)로 수렴하게 된다.)
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 대푯값 (0) | 2022.10.10 |
|---|---|
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 미분법 (0) | 2022.09.27 |
| [확률과 통계] 함수의 극한과 연속 (0) | 2022.09.27 |
| [확률과 통계] 경우의 수 (0) | 2022.09.21 |
| [확률과 통계] 함수 (0) | 2022.09.20 |

