728x90
집합
- 집합은 확률과 통계를 학습하는 데 있어 기본적으로 필요한 개념이므로 집합에 대한 기본적인 개념과 성질에 대한 이해가 필요하다.
집합(Set)
- 집합(Set) : 주어진 조건에 대해서 그 대상을 명확하게 구별할 수 있는 모임
- 원소(Element) : 집합을 구성하는 대상들
- 보편적으로 집합은 대문자 알파벳 `A, B` 등으로 나타내고, 원소는 소문자 알파벳 `a, b` 등으로 나타낸다.
- 집합 `A` 의 원소를 `a, b, c` 라고 할 때, 원소 `a` 가 집합 `A` 에 포함될 경우 `a ∈ A` 와 같이 나타내고, 그렇지 않을 경우 `a \notin A` 로 나타낸다.
- ※ '집합' 을 향하도록 삼지창을 그린다.
집합의 표현
① 원소 나열법(Tabular Form)
- 모든 원소를 나열하는 방법
- 예) `A = {2, 4, 6}`
② 조건 제시법(Set-Builder Form)
- 원소들의 성질들을 조건으로 제시하는 방법
- 예) $A = \{x | x \text{는 짝수}, \; 2 ≤ x ≤ 6\}$
③ 벤 다이어그램(Venn Diagram)
- 서로 다른 집합들 사이의 관계를 표현하는 다이어그램
- 전체 집합과 그 부분 집합의 관계, 또 부분 집합과 부분 집합의 합집합 및 교집합, 그리고 부분 집합의 전체 집합에 관한 여집합 등을 폐곡선으로 나타낸 그림이라고도 표현할 수 있다.

집합의 크기에 따른 분류
① 유한 집합(Finite Set)
- 원소의 개수가 유한한 집합
② 무한 집합(Infinite Set)
- 원소의 개수가 무한한 집합
③ 공집합(Empty Set, $Ø$)
- 원소가 하나도 없는 집합, $n(Ø) = 0, Ø = \{ \}$
- 원소의 개수를 셀 수 있는 것으로 본다. (0개)
- 공집합은 유한 집합이다.
④ 전체 집합(Universal Set, $U$)
- 모든 원소들을 모아둔 집합
부분 집합(Subset)
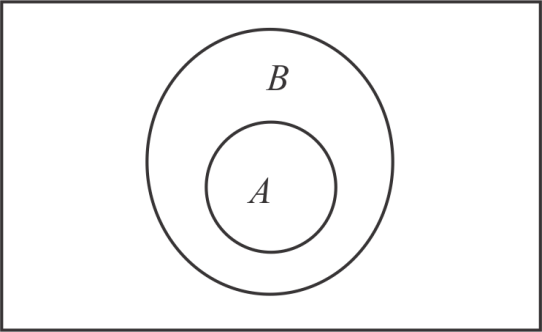
- 두 집합 `A` 와 `B` 에 대해 집합 `A` 의 모든 원소가 집합 `B` 에 속할 때, 집합 `A` 를 집합 `B` 의 부분 집합(Subset)이라 하고, $A ⊂ B$ 로 나타낸다.
- 집합 `A` 가 집합 `B` 의 부분 집합이 아닌 경우에는 $A \not\subset B$ 로 나타낸다.
- $A \subset B$ 이면서 $B\subset A$ 인 두 집합, 즉 집합 `A` 와 `B` 의 원소가 모두 같으면 두 집합 `A` 와 `B` 는 서로 같다(Equal)고 하고 `A = B` 로 나타낸다.
- 그리고 서로 같지 않은 두 집합을 `A ≠ B` 로 나타낸다.
여러 가지 집합
- 두 집합 `A` 와 `B` 의 원소에 의해 새로 구성되는 집합을 살펴보자.
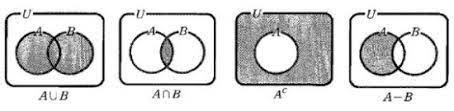
① 교집합(Intersection of Sets)
- 두 집합 `A` 와 `B` 안에 모두 포함된 원소로 구성된 집합을 `A` 와 `B` 의 교집합(Intersection of Sets)이라 하며, 다음과 같이 정의한다.
$$A ∩ B = \{ x | x ∈ A \; \text{그리고} \; x ∈ B \}$$
- 특히, 다음과 같이 공통인 원소를 갖지 않는 두 집합 `A` 와 `B` 를 서로 소(Disjoint)라 한다.
$$A ∩ B = Ø$$
② 합집합(Union of Sets)
- 집합 `A` 또는 `B` 의 원소들로 구성된 집합을 `A` 와 `B` 의 합집합(Union of Sets)이라 하며, 다음과 같이 정의한다.
$$A ∪ B = \{ x | x ∈ A \; \text{또는} \; x ∈ B \}$$
③ 차집합(Difference of Sets)
- 집합 `A` 안에는 포함되지만 집합 `B` 안에는 포함되지 않는 원소로 구성된 집합을 `A` 와 `B` 의 차집합(Difference of Sets)이라 하며, 다음과 같이 정의한다.
$$A - B = \{ x | x ∈ A \; \text{그리고} \; x \not\in B \}$$
④ 여집합(Complementary Set)
- 집합 `A` 안에 포함되지 않는 모든 원소로 구성된 집합을 `A` 의 여집합(Complementary Set)이라 하며, 다음과 같이 정의한다.
$$A^{C} = \{ x | x ∈ U \; \text{그리고} \; x \not\in A \}$$
집합의 성질
- 전체 집합 `U` 와 집합 `A, B, C` 에 대해 다음과 같은 기본적인 집합 연산이 성립한다.
합집합의 성질
(1) $A ∪ A = A$
(2) $A ∪ B = B ∪ A$ (교환 법칙(Distributive Property))
(3) $A ∪ Ø = A$
(4) $A ∪ A^{C} = U$
(5) $A ∪ U = U$
(6) $(A ∪ B) ∪ C = A ∪ (B ∪ C)$ (결합 법칙(Associative Property))
교집합의 성질
(1) $A ∩ A = A$
(2) $A ∩ B = B ∩ A$ (교환 법칙(Distributive Property))
(3) $A ∩ Ø = Ø$
(4) $A ∩ A^{C} = Ø$
(5) $A ∩ U = A$
(6) $(A ∩ B) ∩ C = A ∩ (B ∩ C)$ (결합 법칙(Associative Property))
예 : $A ⊂ B$ 인 경우
- `A` 와 `B` 의 합집합과 교집합은 다음과 같다.
$$A ∪ B = B, \quad A ∩ B = A$$
- 또한 다음과 같이 `A ⊂ B` 인 사건 `B` 를 서로 소인 두 집합 `A` 와 `B - A` 의 합집합으로 표현할 수 있다.
$$B = A ∪ (B - A)$$
기타
여집합의 성질
$$(A^{C})^{C} = A$$
분배 법칙(Distributive Property)
(1) $(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)$
(2) $(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)$
드 모르간의 법칙(De Morgan's Laws)
(1) $(A ∪ B)^{C} = A^{C} ∩ B^{C}$
(2) $(A ∩ B)^{C} = A^{C} ∪ B^{C}$
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
|---|---|
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 적분법 (1) | 2022.10.03 |
| [확률과 통계] 미분법 (0) | 2022.09.27 |
| [확률과 통계] 함수의 극한과 연속 (0) | 2022.09.27 |
| [확률과 통계] 경우의 수 (0) | 2022.09.21 |
| [확률과 통계] 함수 (0) | 2022.09.20 |


