728x90
함수의 극한과 연속
- 함수의 극한(Limit)은 도함수를 정의하기 위한 기초 도구로 사용된다.
- 함수의 연속성은 연속 확률 변수와 확률 분포에서 매우 중요한 역할을 담당한다.
함수의 극한
- 함수 `y = f(x)` 에 대해 변수 `x` 가 실수 `1` 에 한없이 가까워질 때, 함숫값 `f(x)` 가 어떻게 변하는지 살펴보자.
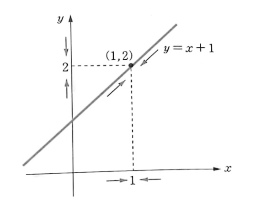
- 함수 `f(x) = x + 1` 은 `x = 1` 에서 함숫값 `f(1) = 2` 가 존재한다.
- 변수 `x` 가 실수 `1` 에 가까워질수록 직선 위의 점은 점 `(1, 2)` 에 가까워진다.
- 따라서 함숫값 `f(x)` 는 `2` 에 가까워지는 것을 알 수 있다.
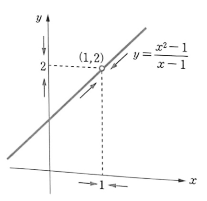
- 한편, 함수 $g(x) = \frac{x^{2}-1}{x-1}$ 은 `x = 1` 에서 함숫값 `g(1)` 이 존재하지 않는다.
- 그러나 `x ≠ 1` 이면 $g(x) = \frac{x^{2}-1}{x-1} = \frac{(x+1)(x-1)}{x-1} = x+1$ 이다.
- 따라서 변수 `x` 가 실수 1에 가까워질수록 직선 위의 점은 점 `(1, 2)` 에 가까워지고, 함숫값 `g(x)` 는 `2` 에 가까워진다.
 |
 |
- 일반적으로 `a` 가 아닌 변수 `x` 가 실수 `a` 에 가까워질수록 함숫값 `f(x)` 가 일정한 값 `L` 에 한없이 가까워진다고 하자.
- 이때 `x` 가 `a` 에 가까워질수록 `f(x)` 는 `L` 에 수렴한다(Converge)고 하고, `L` 을 `x → a` 일 때 함수 `f(x)` 의 극한(Limit)이라 한다. 이를 다음과 같이 나타낸다.
$$\lim_{x→a}f(x) = L \quad \text{또는} \quad x → a \; \text{일 때, } \; f(x) → L$$
- 예를 들어, `x → 1` 일 때 앞의 두 함수 `y = f(x)` 와 `y = g(x)` 는 수렴하고, 극한은 각각 다음과 같다.
$$\lim_{x→1}f(x) = \lim_{x→1}(x + 1) = 2$$
$$\lim_{x→1}g(x) = \lim_{x→1}\frac{x^{2}-1}{x-1} = 2$$
- 특히 `x < a` 이고, `x → a` 일 때 함수 `f(x) → L_{1}` 이면 극한 `L_{1}` 을 좌극한(Left Hand Limit)이라 하고, `x > a` 이고 `x → a` 일 때 함수 `f(x) → L_{2}` 이면 극한 `L_{2}` 를 우극한(Right Hand Limit)이라 한다. 그리고 좌극한과 우극한을 각각 다음과 같이 나타낸다.
$$\lim_{x→a-}f(x) = L_{1}, \quad \lim_{x→a+}f(x) = L_{2}$$
- 따라서 극한이 존재하기 위한 필요 충분 조건은 다음과 같다.
$$\lim_{x→a-} f(x) = \lim_{x→a+} f(x)$$
- 한편, 다음과 같이 함수 $f(x) = \frac{1}{x}$ 은 변수 `x` 가 한없이 커지면 함숫값 `f(x)` 가 `0` 에 한없이 가까워진다.
- 그리고 `x` 가 음수이고 그 절댓값이 한없이 커질 때도 함숫값 `f(x)` 가 `0` 에 한없이 가까워진다.
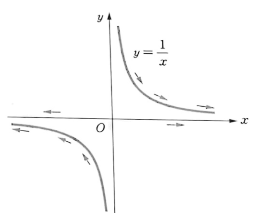
- 일반적으로 `x` 가 한없이 커질 때, 함숫값 `f(x)` 가 일정한 값 `L` 에 한없이 가까워지면 (양의) 무한대에서 `f(x)` 는 `L` 에 수렴한다고 하고, 다음과 같이 나타낸다.
$$\lim_{x→∞}f(x) = L$$
- 그리고 `x` 가 음수이고 그 절댓값이 한없이 커질 때, 함숫값 `f(x)` 가 일정한 값 `L` 에 한없이 가까워지면 음의 무한대에서 `f(x)` 는 `L` 에 수렴한다고 하고, 다음과 같이 나타낸다.
$$\lim_{x→-∞}f(x) = L$$
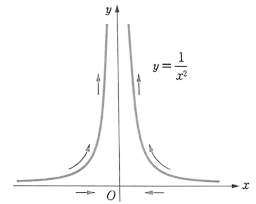
- 함수 $f(x) = \frac{1}{x^{2}}$ 은 `x` 가 `0` 에 가까워질수록 함숫값 `f(x)` 는 한없이 커진다.
- 그리고 함수 $f(x) = -\frac{1}{x^{2}}$ 은 `x` 가 `0` 에 가까워질수록 함숫값 `f(x)` 는 음수이고, 그 절댓값은 한없이 커진다.
 |
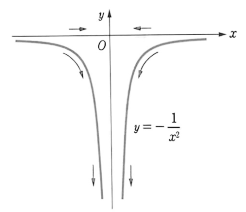 |
- 이와 같이 `x` 가 `a` 에 가까워질수록 함숫값 `f(x)` 가 한없이 커지는 경우에, `x → a` 이면 `f(x)` 는 양의 무한대로 발산한다(Diverge)고 하고, 다음과 같이 나타낸다.
$$\lim_{x→a}f(x) = ∞$$
- 그리고 `x` 가 `a` 에 가까워질수록 함숫값 `f(x)` 가 음수이고, 그 절댓값이 한없이 커지는 경우에, `x → a` 이면 `f(x)` 는 음의 무한대로 발산한다고 하고, 다음과 같이 나타낸다.
$$\lim_{x→a}f(x) = -∞$$
- 한편, `x` 가 한없이 커질수록 `f(x)` 가 한없이 커지는 경우와 `x` 가 음수이고 그 절댓값이 한없이 커질수록 `f(x)` 가 한없이 커지는 경우는 각각 다음과 같이 나타낸다.
$$\lim_{x→∞}f(x) = ∞, \quad \lim_{x→-∞}f(x) = ∞$$
- 끝으로, `x` 가 한없이 커질수록 `f(x)` 가 음수이고, 그 절댓값이 한없이 커지는 경우와 `x` 가 음수이고 그 절댓값이 한없이 커질수록 `f(x)` 가 음수이고 그 절댓값이 한없이 커지는 경우는 각각 다음과 같이 나타낸다.
$$\lim_{x→∞}f(x) = -∞, \quad \lim_{x→-∞}f(x) = -∞$$
- 그러면 함수의 극한에 대해 다음 성질이 성립한다.
$\lim_{x→a}\limits f(x)$ 와 $\lim_{x→a}\limits g(x)$ 가 존재한다면 상수 `k` 에 대해 다음이 성립한다.
(1) $\lim_{x→a}\limits k = k$
(2) $\lim_{x→a}\limits [f(x) ± g(x)] = \lim_{x→a}\limits f(x) ± \lim_{x→a}\limits g(x) $ (복부호 동순)
(3) $\lim_{x→a}\limits [kf(x)] = k \lim_{x→a}\limits f(x)$
(4) $\lim_{x→a}\limits [f(x)g(x)] = (\lim_{x→a}\limits f(x)) \; · \; (\lim_{x→a}\limits g(x)) $
(5) $\lim_{x→a}\limits \frac{f(x)}{g(x)} = \frac{\lim_{x→a}\limits f(x)}{\lim_{x→a}\limits g(x)}, \quad 단 \;\; \lim_{x→a}\limits g(x) ≠ 0$
- 부등호 관계의 서로 다른 함수 `f(x), g(x), h(x)` 에 극한값을 취할 경우, 다음과 같이 나타낼 수 있다.
(1) $f(x) ≤ g(x) ≤ h(x) \Rightarrow \lim_{x→a}\limits f(x) ≤ \lim_{x→a}\limits g(x) ≤ \lim_{x→a}\limits h(x)$
(2) $f(x) < g(x) < h(x) \Rightarrow \lim_{x→a}\limits f(x) ≤ \lim_{x→a}\limits g(x) ≤ \lim_{x→a}\limits h(x)$
[(2) 증명 예] $f(x) = \frac{1}{x}, \quad g(x) = \frac{2}{x}, \quad h(x) = \frac{3}{x}$
- 한편, `a` 를 포함하는 어떤 구간에서 `f(x) ≤ g(x)` 이면 $\lim_{x→a}\limits f(x) ≤ \lim_{x→a}\limits g(x)$ 이고, 다음 정리가 성립되는데 이를 압축 정리(Sandwich Theorem)이라고 한다.
`a` 를 포함하는 어떤 구간에서 $f(x) ≤ g(x) ≤ h(x)$ 이고, $\lim_{x→a}\limits f(x) = \lim_{x→a}\limits h(x) = L$ 이면, $\lim_{x→a}\limits g(x) = L$ 이다.
예제 1 : $\lim_{x→0}\limits x^{2} \sin \frac{1}{x}$ 를 구하라. (단, $-1 ≤ \sin x ≤ 1$ 이다.)
0이 아닌 모든 실수 `x`에 대해 $-1 ≤ sin \frac{1}{x} ≤ 1$ 이므로, `x ≠ 0` 에 대해 `x^{2} > 0` 이다. 따라서 $-x^{2} ≤ x^{2} sin \frac{1}{x} ≤ x^{2}$ 이 성립한다. 또한 $\lim_{x→0}\limits (-x^{2}) = \lim_{x→0}\limits x^{2} = 0$ 이므로, 압축 정리에 의해 $\lim_{x→0}\limits x^{2} \sin \frac{1}{x} = 0$ 이다.
예제 2 : $\lim_{x→∞}\limits \frac{\sin x}{x}$ 를 구하라. (단, $-1 ≤ \sin x ≤ 1$ 이다.)
$-1 ≤ \sin x ≤ 1$ 에서 각 항에 `\frac{1}{x}` 를 곱해준다. 그러면 $-\frac{1}{x} ≤ \frac{\sin x}{x} ≤ \frac{1}{x}$ 이 되는데, $\lim_{x→∞}\limits -\frac{1}{x} = \lim_{x→∞}\limits \frac{1}{x} = 0$ 이므로, 압축 정리에 의해 $\lim_{x→∞}\limits \frac{\sin x}{x} = 0$ 이다.
함수의 연속성
- 특정한 점 `x = a` 에서 함수 `f(x)` 의 함숫값이 존재하든지 그렇지 않든지, `x → a` 일 때 `f(x)` 의 극한은 아무런 관계가 없다.
- 그러나 함수 `f(x) = x + 1` 의 경우에, `x = 1` 에서 함숫값은 `f(1) = 2` 이고, $\lim_{x→1}\limits f(x) = 2$ 이다.
- 즉, $\lim_{x→1}\limits f(x) = f(1)$ 이다.
- 이와 같이 함수 `y = f(x)` 가 다음과 같은 3가지 조건을 만족할 때, 함수 `y = f(x)` 는 `x = a` 에서 연속(Continuous)이라 한다.
① `f(a)` 가 존재한다. (함숫값 존재)
② $\lim_{x→a}\limits f(x)$ 가 존재한다. (극한값 존재)
③ $\lim_{x→a}\limits f(x) = f(a)$ 이다.
- 함수 `y = f(x)` 가 `x = a` 에서 연속이 아닐 때, `y = f(x)` 는 `x = a` 에서 불연속(Discontinuous)이라 한다.
- 한편, `x = a` 에서 연속인 두 함수의 사칙 연산에 대해 다음이 성립한다.
두 함수 `f(x)` 와 `g(x)` 가 `x = a` 에서 연속이면, 다음 함수들도 `x = a` 에서 연속이다.
(1) `kf(x)`
(2) `f(x) + g(x)`
(3) `f(x) - g(x)`
(4) `f(x)g(x)`
(5) $\frac{f(x)}{g(x)} \quad 단, \; g(a) ≠ 0$
- 함수 `f(x)` 가 어떤 구간 안의 모든 점에서 연속이면, 간단히 함수 `f(x)` 는 구간에서 연속이라 한다.
- 특히, 함수 `f(x)` 가 개구간 `(a, b)` 에서 연속이고 양 끝점에서 다음이 성립하면, 함수 `f(x)` 는 폐구간 `[a, b]` 에서 연속이라 한다.
$$\lim_{x→a+} f(x) = f(a), \quad \lim_{x→b-} f(x) = f(b)$$
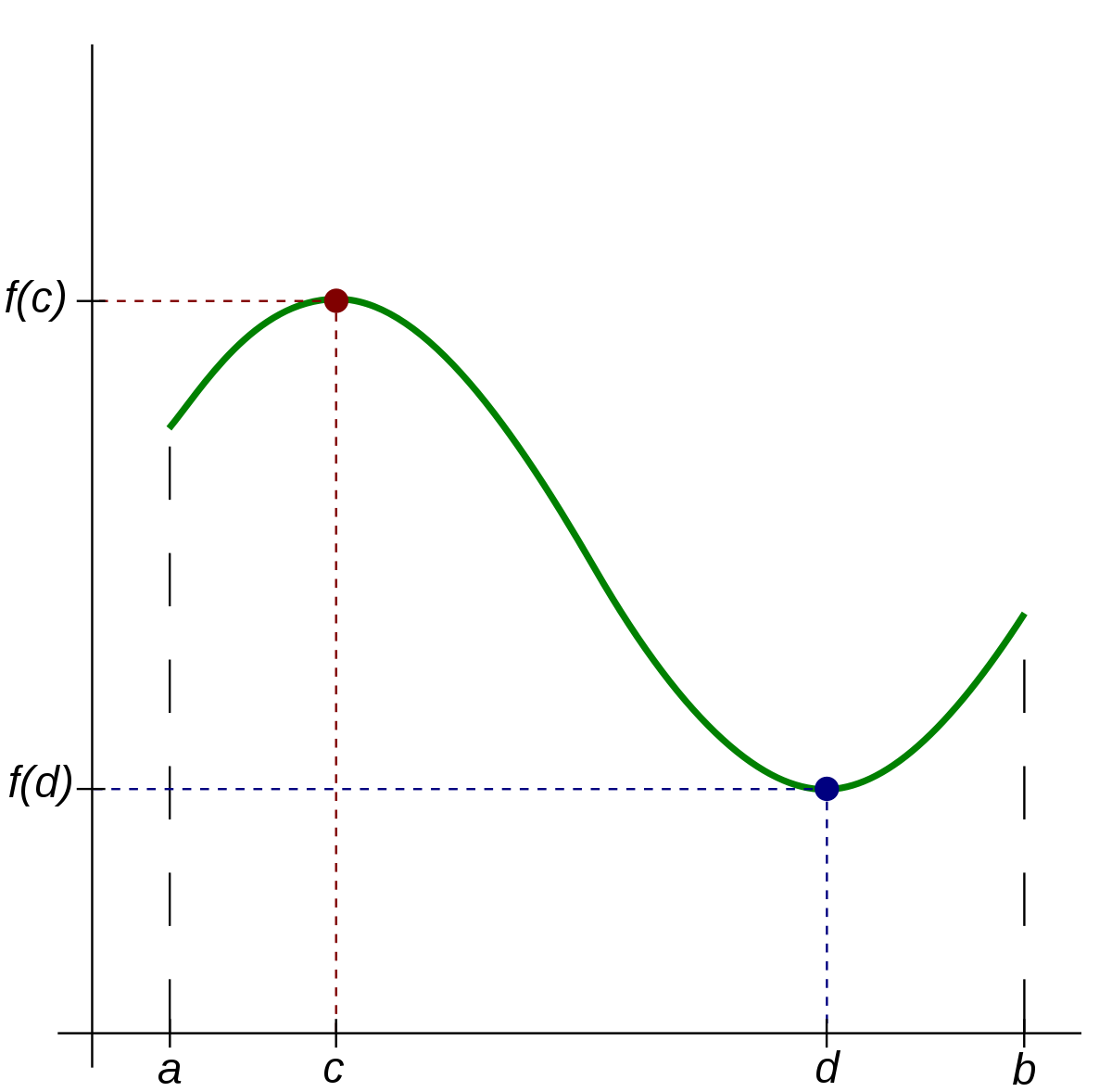
최대 최소 정리(Min-Max Theorem)
함수 `f(x)` 가 폐구간 `[a, b]` 에서 연속이면, 폐구간 `[a, b]` 에서 함수 `f(x)` 의 최댓값과 최솟값이 반드시 존재한다.
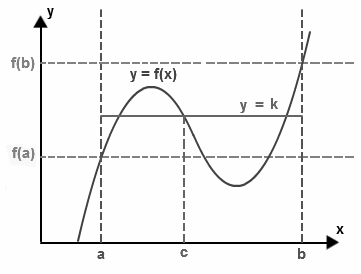
중간값 정리(Intermediate Value Theorem)
- '사잇값 정리' 라고도 불린다.
함수 `f(x)` 가 폐구간 `[a, b]` 에서 연속이고, `f(a) ≠ f(b)` 이면, `f(a)` 와 `f(b)` 사이의 임의의 실수 `k` 에 대해 `f(c) = k` 를 만족하는 `c` 가 개구간 `(a, b)` 안에 적어도 하나 존재한다.
- 방정식의 근의 존재성을 보일 때 많이 활용된다.
- 예) `x^{2} + x + 1 = 0`
- `f(x) = x^{3} + x + 1`
`f(0) = 1 > 0, f(-1) = -1 < 0`
`f(x)` 가 `[-1, 1]` 에서 연속
'중간값 정리'에 의해서 `f(c) = 0` 인 $c \in (-1, 0)$ 에 존재
- `f(x) = x^{3} + x + 1`
- 예) `x^{2} + x + 1 = 0`
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
|---|---|
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 적분법 (1) | 2022.10.03 |
| [확률과 통계] 미분법 (0) | 2022.09.27 |
| [확률과 통계] 경우의 수 (0) | 2022.09.21 |
| [확률과 통계] 함수 (0) | 2022.09.20 |
| [확률과 통계] 집합 (1) | 2022.09.15 |


