728x90
함수
- 확률 현상에서 발생하는 특정한 성질을 나타내기 위해 확률 변수를 사용하는데, 이때 확률 변수에 대한 함수를 이용하면 확률을 쉽게 계산할 수 있다.
함수의 의미
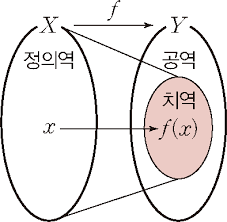
- 공집합이 아닌 두 집합 `X` 와 `Y` 에 대해 `X` 안의 각 원소 `x` 를 `Y` 안에 있는 오직 한 원소 `y` 에 대응시키는 관계 `f` 를 함수(Function)라 하고, $f : X → Y, \; y = f(x)$ 로 나타낸다.
- `x` 의 집합 `X` 를 함수 `f` 의 정의역(Domain)이라 하고 $dom(f)$(또는 $D_{f}$) 로 나타낸다.
- `y` 의 집합 `Y` 를 함수 `f` 의 공역(Codomain)이라 한다.
- 특히 `y = f(x)` 를 함수라 하면, `x` 값이 정해지면 대응 관계 `f` 에 의해 `y` 값이 오직 하나만 정해진다.
- `x` : 독립 변수(Independent Variable)
- `y` : 종속 변수(Dependent Variable) 또는 `x` 의 함숫값(Value of Function)
- 다음과 같이 집합 `X` 안의 모든 원소 `x` 에 대한 함숫값들의 집합을 함수 `f` 의 치역(Range)이라 하고, `f(X)` 또는 $ran(f)$(또는 $R_{f}$) 로 나타낸다.
$$f(X) = \{y | y = f(x), \; x ∈ X\}$$
- 그러면 `X` 에서 `Y` 로의 함수 `f` 에 대해 `f` 의 치역은 공역 `Y` 의 부분 집합, 즉 $f(X) ⊆ Y$ 이다.
- 또한 `X` 에서 `Y` 로의 함수 `y = f(x)` 에 대해 순서쌍 `(x, y)` 전체의 집합을 함수 `y = f(x)` 의 그래프(Graph)라고 한다.
$$G = \{ (x, y) | y = f(x), \; x ∈ X \}$$
- 이때 정의역 안의 모든 원소가 공역 안의 한 원소와 대응을 이루는 함수 $y = f(x) = a, \; a ∈ Y$ 를 상수 함수(Constant Function)라 하고, 자기 자신으로 대응을 이루는 함수 $y = f(x) = x$ 를 항등 함수(Identity Function)라 한다.
함수의 연산과 합성
- 함수에서는 의미가 같지만, 표현을 다르게 할 수 있다.
- 그리고 어떤 함수들이 주어지면, 그 함수들을 이용하여 새로운 함수를 만들 수 있다.
함수의 상등
- 실수 전체의 집합 `R` 에서 `R` 로의 함수 $f : R → R$ 과 $g : R → R$ 을 생각해보자.
- 이때 두 함수 `f` 와 `g` 가 다음 두 조건을 만족하면, 두 함수 `f` 와 `g` 는 서로 상등(Equal)이라 하고 `f = g` 로 나타낸다.
- 이때 두 함수 `f` 와 `g` 가 상등이 아니면, `f` 와 `g` 는 서로 같지 않다고 하며 `f ≠ g` 로 나타낸다.
① 두 함수의 정의역이 같다. ($dom(f) = dom(g)$)
② 정의역 안의 모든 원소 `x` 에 대한 함숫값이 같다. ($f(x) = g(x)$)
함수의 연산
- 두 함수 `f` 와 `g` 에 대해 다음과 같이 사칙 연산을 적용하여 새로운 함수를 만들 수 있다.
- 이때 사칙 연산에 의해 생성된 새로운 함수는 두 함수의 정의역의 교집합에서 정의된 것에 유의해야 한다.
| 함수의 사칙 연산 | 정의역 |
| (1) $(f + g)(x) = f(x) + g(x)$ | $dom(f+g) = dom(f) ∩ dom(g)$ |
| (2) $(f - g)(x) = f(x) - g(x)$ | $dom(f-g) = dom(f) ∩ dom(g)$ |
| (3) $(f·g)(x) = f(x)·g(x)$ | $dom(f·g) = dom(f) ∩ dom(g)$ |
| (4) $ \left( \frac{f}{g} \right) = \frac{f(x)}{g(x)}$ | $dom(f / g) = dom(f) ∩ dom(g) - \{x | g(x) = 0\}$ |
- 또한 함수 `f` 와 영이 아닌 실수 `k` 의 곱을 다음과 같이 정의한다.
- `k > 0` 에 대해 함수 `kf` 는 함수 `f` 를 `k` 배 만큼 늘리거나 줄인 함수이다.
- `k < 0` 에 대해 함수 `kf` 는 함수 `f` 를 `x` 축에 대해 대칭 이동하여 `k` 배 만큼 늘리거나 줄인 함수이다.
$$(kf)(x) = kf(x), \quad dom(kf) = dom(f)$$
함수의 합성
- 두 함수 $f : X → Y$ 와 $g : Y → Z$ 에 대해 다음과 같이 함수 `f` 에 의해 $x ∈ X$ 가 $y = f(x) ∈ Y$ 에 대응하고, 이 원소 `y` 가 함수 `g` 에 의해 `z = g(y) ∈ Z` 로 대응한다고 하자.
- 그러면 집합 `X` 의 원소 `x` 는 집합 `Z` 의 원소 `z` 로 대응을 이룬다.
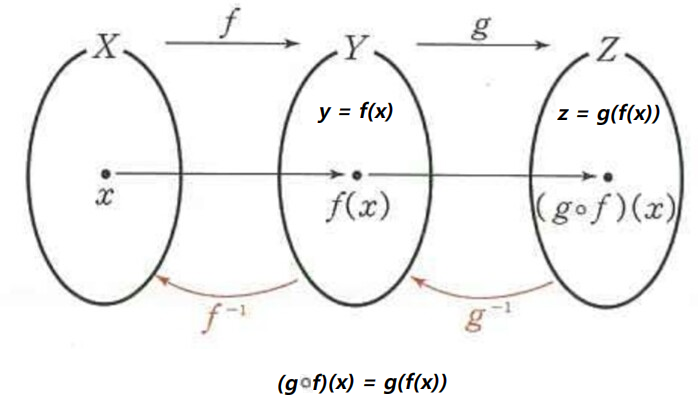
- 이때 집합 `X` 로부터 집합 `Z` 로의 함수를 `g` 와 `f` 의 합성 함수(Composite Function)라 하고, 다음과 같이 나타낸다.
$$g \circ f : X → Z, \quad (g \circ f)(x) = g(f(x))$$
일차 함수와 이차 함수
일차 함수(Linear Function)
- 상수 $a \; (a ≠ 0)$ 에 대해 함수 $y = ax + b$ 를 일차 함수(Linear Function)라 하며, 일차 함수의 그래프는 다음과 같이 직선이다.
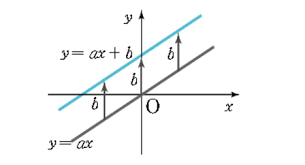
- 이때 상수 `a` 를 기울기(Slope)라 하며, 기울기는 `x` 가 1만큼 증가할 때 `y` 가 `a` 만큼 증가하거나 감소함을 나타낸다.
- 기울기가 양수이면(`a > 0`), `x` 가 1 만큼 증가할 때 `y` 는 `a` 만큼 증가한다.
- 기울기가 음수이면(`a < 0`), `x` 가 1만큼 증가할 때 `y` 는 `|a|` 만큼 감소한다.
- `x = 0` 이면, `y = b` 이고 직선이 `y` 축을 절단한다.
- `y = b` 를 `y`-절편(y-Intercept)라 한다.
- `y = 0` 이면, `x = -\frac{b}{a}` 이고 직선이 `x` 축을 절단한다.
- `x = -\frac{b}{a}` 를 `x`-절편(x-Intercept)라 한다.
이차 함수(Quadratic Function)
- 상수 $a \; (a ≠ 0), b, c$ 에 대해 함수 $y = ax^{2} + bx + c$ 를 이차 함수(Quadratic Function)라 하며, 일차 함수의 그래프는 다음과 같이 포물선이다.
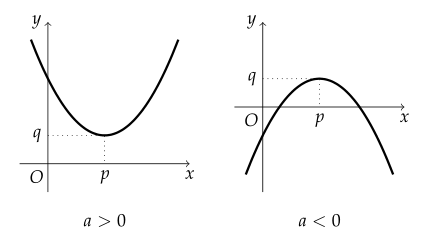
- 이차항의 계수 `a` 는 이차 함수의 기울기를 나타내고, 상수 `c` 는 `y`-절편을 나타낸다.
- `a > 0` 이면 아래로 볼록한 포물선이고, `a < 0` 이면 위로 볼록한 포물선이다.
$y = a(x - p)^{2} + q$
- 이차 함수 `y = ax^{2}` 은 `y` 축에 대해 좌우 대칭이고, 꼭짓점의 좌표는 `(0, 0)` 이다.
- `y = ax^{2}` 을 `y` 축을 따라 `q` 만큼 평행 이동하면 `y = ax^{2} + q` 이고, 이 함수의 그래프는 `y` 축에 대해 좌우 대칭이고 꼭짓점의 좌표는 `(0, q)` 이다.
- `y = ax^{2} + q` 를 `x` 축을 따라 오른쪽으로 `p` 만큼 평행 이동한 함수는 `y = a(x - p)^{2} + q` 이고, 이 함수의 그래프는 `x = p` 에 대해 좌우 대칭이고, 꼭짓점의 좌표가 `(p, q)` 이다.
- 완전 제곱식을 이용하여 함수 `y = ax^{2} + bx + c` 를 다음과 같이 `y = a(x - p)^{2} + q` 의 형태로 고칠 수 있다.
$$y = ax^{2} + bx + c = a \left( x + \frac{b}{2a} \right)^{2} - \frac{b^{2} - 4ac}{4a}$$
- 그러면 `p = -\frac{b}{2a}`, `q = -\frac{b^{2}-4ac}{4a}` 이다.
- `a > 0` 이면 꼭짓점에서 이차 함수는 최솟값을 가지며, `a < 0` 이면 꼭짓점에서 이차 함수는 최댓값을 가진다. 이때 최댓값 또는 최솟값은 다음과 같다.
$$f(p) = - \frac{b^{2}-4ac}{4a}$$
요약
함수 $f : X → Y$
- 공집합이 아닌 두 집합 `X` 와 `Y` 에 대하여 `X` 의 각 원소 `x` 를 `Y` 의 오직 한 원소 `y` 에 대응시키는 관계
- `X` : 정의역
- `Y` : 공역
- `f(x) = \{ f(x) | x ∈ X \}` : 치역
- `G = \{ (x, f(x) | x ∈ X \}` : 그래프
함수의 종류
- 상수 함수(Constant Function) : 함숫값이 상수인 함수 ($f(x) = c (c ∈ \mathbb{R}$)
- 항등 함수(Identity Function) : 임의의 `x ∈ X` 에 대하여 `f(x) = x` 인 함수 ($X ⊂ Y$)
- 일대일 함수(One-to-One Function; 단사 함수(Injective Function)) : `x_{1} ≠ x_{2} \Rightarrow f(x_{1}) ≠ f(x_{2})` 인 함수
- `f(x_{1}) = f(x_{2}) \Rightarrow x_{1} = x_{2}` 인 함수
- 전사 함수(Surjective Function) : `f(X) = Y` 인 함수 (치역 = 공역)
- 일대일 대응 함수(Bijective Function) : 일대일 함수이면서 전사 함수인 함수
함수의 상등
$f = g$
① $D_{f} = D_{g}$ (두 함수의 정의역이 같다.)
② $\forall{x} ∈ D_{f} = D_{g}, \quad f(x) = g(x)$
예제 : 다음 함수들의 정의역을 구하고, 두 함수가 같은지 결정하여라.
(1) $f(x) = x, \quad g(x) = \sqrt[3]{x}$
(2) $f(x) = (\sqrt{x})^{2}, \quad g(x) = \sqrt{x^{2}}$
(1)
$D_{f} = \mathbb{R}, \; D_{g} = \mathbb{R}$ 이므로 두 함수의 정의역은 같다. 따라서 함수의 상등 조건 ①을 만족시킨다.
$f(8) = 8, \; g(8) = 2$ 이므로 $f(8) ≠ g(8)$ 이므로, 두 함수의 함숫값이 다르다. 따라서 함수의 상등 조건 ②를 만족시키지 못한다.
따라서 두 함수는 상등이 아니다.
(2)
$D_{f} = [0, ∞], \; D_{g} = \mathbb{R}$ 이므로 두 함수의 정의역은 다르다. 따라서 함수의 상등 조건 ①을 만족시키지 못한다.
따라서 두 함수는 상등이 아니다.
함수의 연산
$D_{f} = X, \; D_{g} = Y$
(1) $(f ± g)(x) = f(x) ± g(x), \quad D_{f±g} = X ∩ Y$
(2) $(cf)(x) = c·f(x) \; (c ∈ \mathbb{R}), \quad D_{cf} = X$
(3) $(fg)(x) = f(x)g(x), \quad D_{fg} = X ∩ Y$
(4) $\displaystyle \left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)} \quad D_{\frac{f}{g}} = X ∩ (Y - \{x | g(x) = 0 \})$
함수의 합성
$f : X → Y, \; g : Y → Z \Rightarrow g \circ f : X → Z \quad (x ∈ X)$
$ g \circ f(x) = g(f(x))$
$f \circ g ≠ g \circ f$ (교환 법칙 성립 X)
$f \circ (g \circ h) = (f \circ g) \circ h$ (결합 법칙 성립 O)
일차 함수와 이차 함수
일차 함수
$y = ax + b$ : 직선
- `a` : 기울기
- `b` : y절편
이차 함수
$y = ax^{2} + bx + c$
$= a(x - p)^{2} + q$
$= a(x - s)(x - t)$
$a > 0$ : 아래로 볼록
$a < 0$ : 위로 볼록
- 축의 방정식 : `x = p`
- 꼭짓점 : `(p, q)`
- x절편 : `s, t`
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
|---|---|
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 적분법 (1) | 2022.10.03 |
| [확률과 통계] 미분법 (0) | 2022.09.27 |
| [확률과 통계] 함수의 극한과 연속 (0) | 2022.09.27 |
| [확률과 통계] 경우의 수 (0) | 2022.09.21 |
| [확률과 통계] 집합 (1) | 2022.09.15 |


