경우의 수
- 어떤 상황에 부딪혔을 때, 그 상황에서 나타날 수 있는 모든 경우의 수를 생각해야 할 때가 빈번히 발생한다.
합의 법칙과 곱의 법칙
합의 법칙(Rule of Addition)
- 서로 소인 두 집합 `A` 와 `B` 의 원소의 수를 각각 `n(A)`, `n(B)` 라고 하면, 두 집합이 서로 소이므로 합집합 `A ∪ B` 의 원소의 개수는 `n(A ∪ B) = n(A) + n(B)` 이다.
- 이와 같이 동시에 발생하지 않는 두 사건 `A` 와 `B` 가 일어나는 경우의 수를 각각 `m` 과 `n` 이라 할 때, 사건 `A` 또는 사건 `B` 가 일어나는 경우의 수는 `m + n` 이고, 이를 합의 법칙 (Rule of Addition)이라 한다.
예제 1 : 책상 위에 서로 다른 연필 5자루와 서로 다른 볼펜 4자루가 있을 때, 둘 중 하나를 선택 하는 경우의 수 구하기
- `A` :연필 한 자루를 선택하는 사건
- `B` : 볼펜 한 자루를 선택하는 사건
- $n(A) = 5, \; n(B) = 4$ 이므로 `n(A ∪ B) = 9`
예제 2 : 주사위를 두 번 던져서 나온 눈의 수의 합이 소수인 경우의 수 구하기
- `x` : 주사위를 두 번 던져서 첫 번째 나온 눈의 수
- `y` : 주사위를 두 번 던져서 두 번째 나온 눈의 수
- `x = 1, 2, 3, 4, 5, 6`, `y = 1, 2, 3, 4, 5, 6` 이므로 `x + y = 2, 3, …, 12` 이다.
- 12 이하의 소수는 `2, 3, 5, 7, 11` 뿐이므로 `x + y` 가 소수인 경우는 다음과 같다.
- $x + y = 2 \Rightarrow (x, y) = (1, 1)$ [1가지]
- $x + y = 3 \Rightarrow (x, y) = (1, 2), (2, 1)$ [2가지]
- $x + y = 5 \Rightarrow (x, y) = (1, 4), (4, 1), (2, 3), (3, 2)$ [4가지]
- $x + y = 7 \Rightarrow (x, y) = (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3)$ [6가지]
- $x + y = 11 \Rightarrow (x, y) = (5, 6), (6, 5)$ [2가지]
- 각각의 경우는 동시에 나타나지 않으므로 구하고자 하는 경우의 수는 15가지이다.
곱의 법칙(Rule of Multiplication)
- 사건 `A` 가 일어나는 모든 경우의 수가 `m` 이고, 사건 `A` 가 일어나는 각각의 경우에 대해 사건 `B` 가 일어나는 경우의 수가 `n` 이라 할 때, 두 사건 `A` 와 `B` 가 동시에 일어나는 경우의 수는 `m × n` 이고, 이를 곱의 법칙(Rule of Multiplication)이라 한다.
예제 1 : 주사위를 두 번 던져서 나올 수 있는 모든 경우의 수 구하기
- `x` : 주사위를 던졌을 때 첫 번째 나온 눈의 수
- `y` : 주사위를 던졌을 때 두 번째 나온 눈의 수
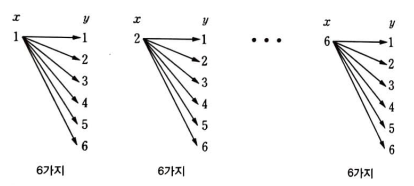
- 처음에 나온 눈의 수는 1, 2, 3, 4, 5, 6 으로 6가지이고, 그 각각에 대해 두 번째 나온 눈의 수가 6가지 있다.
- 따라서 주사위를 두 번 던져서 나올 수 있는 모든 경우의 수는 곱의 법칙에 의해 36가지이다.
예제 2 : 한 평면 위에 어느 세 점도 한 직선 위에 놓여 있지 않은 서로 다른 점이 5개 있을 때, 두 점을 연결하여 만들 수 있는 서로 다른 선분의 개수 구하기
- 5개의 점을 `A, B, C, D, E` 라 할 때, 점 `A` 에서 그을 수 있는 선분의 개수는 다음과 같이 4개이다.
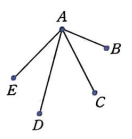
- 그리고 `B, C, D, E` 에서 그을 수 있는 선분의 개수도 각각 4개씩이므로, 구하고자 하는 경우의 수는 `4 × 5 = 20` 이다.
- 이때 선분 $\overline{AE}$ 와 선분 $\overline{ EA }$ 와 같이 동일한 선분이 2번 나타나므로, 구하고자 하는 서로 다른 선분의 개수는 $\frac{20}{2} = 10$ (개)이다.
순열(Permutation)
- 4개의 문자 `A, B, C, D` 를 `ABCD` 또는 `BADC` 등과 같이 서로 다르게 배열하는 방법을 생각해보자. 다음과 같이 4개의 문자를 이용하여 배열할 수 있는 모든 경우의 수는 24가지이다.
| ABCD | ABDC | ACBD | ACDB | ADBC | ADCB |
| BACD | BADC | BCAD | BCDA | BDAC | BDCA |
| CABD | CADB | CBAD | CBDA | CDAB | CDBA |
| DABC | DACB | DBAC | DBCA | DCAB | DCBA |
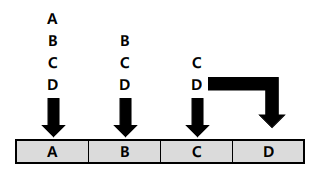
- 이때 4개의 문자 `A, B, C, D` 를 이용하여 위와 같이 서로 다르게 배열한 각각의 경우보다 배열할 수 있는 가짓수에 관심을 갖는다고 하자. 이런 가짓수는 위와 같이 생각하여 구할 수 있다.
- 첫 번째 상자에는 `A, B, C, D` 중에서 어느 것이든 넣을 수 있으므로 첫 번째 상자에 문자를 넣는 방법은 4가지이다.
- 만약 첫 번째 상자에 문자 `A` 를 넣었다고 하면, 두 번째 상자에는 `A` 를 제외한 `B, C, D` 중에서 어느 하나를 넣을 수 있으므로 3가지 방법이 있다.
- 이제 두 번째 상자에 문자 `B` 를 넣었다면, 세 번째 상자에 `C` 또는 `D` 중에서 어느 하나를 넣을 수 있으므로 2가지 방법이 있으며, 마지막 상자에는 세 번째 상자에 넣지 않은 문자 하나를 넣을 수 있으므로 자동적으로 1가지 방법 밖에 없다.
- 따라서 문자 `A, B, C, D` 를 서로 다르게 나열 할 수 있는 경우의 수는 곱의 법칙에 의해 `4 × 3 × 2 × 1 = 24`(가지)이다.
- `4 × 3 × 2 × 1 = 24` 를 `4! = 24` 로 나타내며, 다음과 같이 `1` 부터 `n` 까지 연속인 자연수들의 곱을 `n` 계승(Factorial)이라 한다. 단, `0! = 1` 로 약속한다.
$$n! = 1 × 2× × … × (n - 1) × n$$
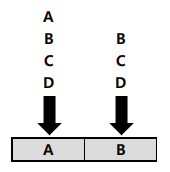
- 한편, 4개의 문자 `A, B, C, D` 중에서 서로 다른 문자 2개를 택하여 `AB, BA` 등과 같이 순서대로 나열하는 방법의 수를 생각할 수 있다.
- 이 방법의 수는 다음과 같이 두 상자에 문자 두 개를 순서대로 넣는 경우와 동일하다.
- 이때, 첫 번째 상자에 넣을 수 있는 문자는 `A, B, C, D` 중에서 어느 하나이므로 4가지 방법이 있다.
- 만일 문자 `A` 를 첫 번째 상자에 넣었다면, 두 번째 상자에는 `A` 를 제외한 나머지 문자 `B, C, D` 중에서 어느 하나를 넣을 수 있으므로 3가지 방법이 있다.
- 따라서 문자 4개 중에서 서로 다른 문자 2개를 선택하여 순서대로 나열할 수 있는 경우의 수는 `4 × 3 = 12`(가지)이다.
- 이와 같이 서로 다른 `n` 개에서 `r` 개를 선택하여 순서대로 나열하는 방법을 순열(Permutation)이라 하고, 순열의 수를 $_{n}P_{r}$ 로 나타낸다.
- 예를 들어, 서로 다른 4개 중에서 2개를 선택하여 순서대로 나열하는 방법의 수는 $_{4}P_{2} = 4 × 3 = 12$ 이다.
- 이제 서로 다른 `n` 개에서 `r` 개를 선택하는 순열의 수 $_{n}P_{r}$ 을 구하기 위해 상자 `r` 개를 생각해보자.
- 그러면 첫 번째 상자에 넣을 수 있는 경우의 수는 `n` 가지이고, 이 중에서 어느 하나를 넣었다면 두 번째 상자에 넣을 수 있는 경우의 수는 `n - 1` 가지이다.
- 그리고 세 번째 상자에 넣을 수 있는 경우의 수는 처음 두 상자에 넣은 것을 제외한 `n - 2` 가지이다.
- 이와 같이 반복하여 마지막 `r` 번째 상자에 넣을 수 있는 경우의 수는 `n - r + 1` 가지이다.
- 따라서 서로 다른 `n` 개에서 `r` 개를 선택하는 순열의 수, $_{n}P_{r}$ 은 곱의 법칙에 의해 다음과 같다.
$$_{n}P_{r} = n(n - 1)(n - 2) \cdots (n - r + 1)$$
- 특히, `r = n` 이면 $_{n}P_{n} = n!$ 이다.
- 순열의 수는 계승을 이용하여 다음과 같이 나타낼 수 있다.
$$_{n}P_{r} = n(n - 1)(n - 2) \cdots (n - r + 1)$$
$$= \frac{n(n - 1) \cdots (n - r + 1)(n - r)(n - r - 1) \cdots 2 × 1}{(n - r)(n - r - 1) \cdots 2 × 1}$$
$$= \frac{n!}{(n -r)!}$$
- 또한, `0! = 1` 로 약속했으므로, 이 식에서 `r = 0` 이라 하면 $_{n}P_{0} = 1$ 이다. 그러므로 순열의 수는 다음과 같이 간단히 나타낼 수 있다.
$$_{n}P_{r} = \frac{n!}{(n - r)!}, \quad r = 0, 1, \cdots, n$$
- 그러면 순열의 수는 다음의 성질을 갖는다.
$r = 1, 2, \cdots, n$ 에 대해 다음이 성립한다.
(1) $n × _{n-1}P_{r-1} = \; _{n}P_{r}$
(2) $_{n-1}P_{r} + r × _{n-1}P_{r-1} = \; _{n}P_{r}$
예제 : 숫자 0, 1, 2, 3, 4, 5에서 서로 다른 숫자 3개를 선택하여 세 자리 숫자를 만든다고 할 때, 다음을 구하라.
(a) 일의 자리가 0인 짝수의 개수
(b) 일의 자리가 2인 짝수의 개수
(c) 일의 자리가 4인 짝수의 개수
(d) 세 자리 숫자가 짝수인 개수
(a) 백의 자리와 십의 자리에 1, 2, 3, 4, 5 중에서 서로 다른 2개를 선택하면 된다. 따라서 일의 자리가 0인 짝수의 개수는 $_{5}P_{2} = 5 × 4 = 20$(개) 이다.
(b) 백의 자리에 올 수 있는 숫자는 0을 제외한 1, 3, 4, 5 중에서 하나이므로 4가지가 있다. 그리고 십의 자리에 올 수 있는 숫자는 백의 자리에 온 숫자를 제외한 4개의 숫자 중에서 어느 하나이다. 따라서 일의 자리가 2인 짝수의 개수는 `4 × 4 = 16`(개)이다.
(c) (b)에서 숫자 2를 숫자 4로 바꾼 경우이므로 경우의 수는 `16`(개) 이다.
(d) 세 자리 숫자가 짝수인 경우는 일의 자리가 0, 2, 4인 경우이므로 세 자리 숫자가 짝수인 개수는 `20 + 16 + 16 = 52`(개)이다.
조합(Combination)
- 4개의 문자 `A, B, C, D` 중에서 순서를 생각하지 않고 서로 다른 문자 2개를 택한다면, `AB` 와 `BA` 는 순서를 생각하지 않으므로 동일한 경우가 된다.
- 따라서 4개의 문자 중에서 순서 없이 서로 다른 두 문자를 선정한 모든 경우는 `AB, AC, AD, BC, BD, CD` 뿐이고, 이 경우의 수는 6가지이다.
- 즉, 서로 다른 4개의 문자 중에서 순서대로 2개를 선정한 12개 중에서 순서를 무시하면 동일한 문자의 배열이 2개씩 있다.
- 그러므로 4개의 문자 중에서 순서 없이 서로 다른 두 문자를 선정한 모든 경우의 수는 $\frac{_{4}P_{2}}{2} = \frac{12}{2} = 6$(가지) 이다.
- 이와 같이 서로 다른 `n` 개 중에서 순서를 생각하지 않고 `r` 개를 선택하는 방법을 조합(Combination)이라 하고, 조합의 수를 $_{n}C_{r}$ 로 나타낸다.
- 일반적으로 서로 다른 `n` 개 중에서 `r` 개를 선택하는 조합의 수는 다음과 같다. 이때 $_{n}C_{0} = 1$ 로 정의한다.
$$_{n}C_{r} = \frac{_{n}P_{r}}{r!} = \frac{n!}{r!(n-r)!}$$
- $_{n}C_{r} = \frac{_{n}P_{r}}{r!}$ 이므로, 다음과 같이 순열과 조합의 관계를 나타낼 수 있다.
$$_{n}P_{r} = \; _{n}C_{r} × r!$$
- 그러면 조합의 수는 다음의 성질을 갖는다.
(1) $r = 0, 1, \cdots, n$ 에 대해 $\; _{n}C_{r} \; = \; _{n}C_{n-r}$ 이다.
(2) $r = 1, 2, \cdots, n - 1$ 에 대해 $\; _{n-1}C_{r} \; + \; _{n-1}C_{r-1} \; = \; _{n}C_{r}$ 이다.
- 이와 같은 조합의 수를 이용하면 $(a + b)^{n}$ 을 전개한 식을 쉽게 얻을 수 있다.
$(a + b)^{1} = \; _{1}C_{0}a + \; _{1}C_{1}b$
$(a + b)^{2} = \; _{2}C_{0}a^{2} + \; _{2}C_{1}ab + \; _{2}C_{2}b^{2} $
$(a + b)^{3} = \; _{3}C_{0}a^{3} + \; _{3}C_{1}a^{2}b + \; _{3}C_{2}ab^{2} + \; _{3}C_{3}b^{3} $
$(a + b)^{4} = \; _{4}C_{0}a^{4} + \; _{4}C_{1}a^{3}b + \; _{4}C_{2}a^{2}b^{2} + \; _{4}C_{3}ab^{3} + \; _{4}C_{4}b^{4} $
- 일반적으로 $(a + b)^{n}$ 의 전개식에서 조합의 수를 이용하여 계수를 나타내면 다음을 얻는다. 이를 이항 정리(Binomial Theorem)이라 한다.
자연수 `n` 에 대해 다음이 성립한다.
$$(a + b)^{n} = \; _{n}C_{0}a^{n}b^{0} + \; _{n}C_{1}a^{n - 1}b^{1} + \; _{n}C_{2}a^{n - 2}b^{2} + \cdots + \; _{n}C_{n-1}a^{1}b^{n-1} + \; _{n}C_{n}a^{0}b^{n}$$
$$= \; _{n}C_{0}a^{n}b^{0} + \; _{n}C_{n - 1}a^{n - 1}b^{1} + \; _{n}C_{n - 2}a^{n - 2}b^{2} + \cdots + \; _{n}C_{1}a^{1}b^{n-1} + \; _{n}C_{0}a^{0}b^{n}$$
예제 : 남학생 7명과 여학생 5명인 동아리에서 남학생 3명과 여학생 2명을 선정하는 경우의 수를 구하라.
남학생 7명 중에서 3명을 선정하는 방법의 수는 $_{7}C_{3} = \frac{7!}{3! × 4!} = 35$(가지)이다. 그리고 그 각각에 대해 여학생 5명 중에서 2명을 선정하는 방법의 수는 $_{5}C_{2} = \frac{5!}{2! × 3!} = 10$(가지)이다. 따라서 구하고자 하는 경우의 수는 $35 × 10 = 350(가지)$이다.
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
|---|---|
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 자료의 종류 (0) | 2022.10.03 |
| [확률과 통계] 적분법 (1) | 2022.10.03 |
| [확률과 통계] 미분법 (0) | 2022.09.27 |
| [확률과 통계] 함수의 극한과 연속 (0) | 2022.09.27 |
| [확률과 통계] 함수 (0) | 2022.09.20 |
| [확률과 통계] 집합 (1) | 2022.09.15 |


