이산 확률 변수
이산 확률 변수의 의미
- 동전을 두 번 던지는 게임에서 앞면이 나온 횟수를 `X` 로 나타내면, `X` 를 이용하여 앞면이 나온 횟수라는 특성에 따라 구분된 사건을 다음과 같이 간단히 표현할 수 있다.
| $$ \eqalign{ \{ HH \} &\Leftrightarrow X = 2 \\ \{ HT, TH \} &\Leftrightarrow X = 1 \\ \{ TT \} &\Leftrightarrow X = 0}$$ |
- 그러므로 앞면이 나온 횟수인 `X` 는 아래와 같이 표본 공간 `S` 에서 실수 전체의 집합 `R` 로의 함수로 생각할 수 있다.
- 이 때 앞면이 나온 횟수인 `X` 를 확률 변수(Random Variable)라고 한다.
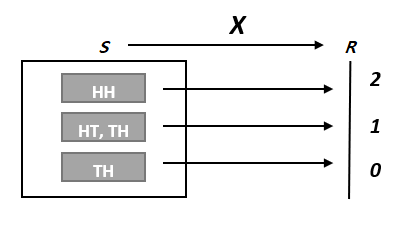
확률 변수(Random Variable)
표본 공간 `S` 안의 원소에 실수를 대응시키는 함수를 확률 변수(Random Variable)라 하며, 보통 `X` 와 같이 대문자로 나타낸다.
- 표본 공간 안의 원소를 확률 변수로 나타내면, 표본 공간을 간단히 표현할 수 있다.
- 예) 앞의 확률 변수 `X` 가 취할 수 있는 모든 값은 $\{0, 1, 2 \}$ 뿐이다.
- 이 때, 확률 변수 `X` 가 취할 수 있는 모든 가능한 숫자들의 집합을 상태 공간(State Space)이라 하고, $S_{X}$ 로 나타낸다.
- 동전 두 번 던지기와 같은 경우에는 `X` 의 상태 공간을 구성하는 숫자는 3개뿐이다. ($\{HH, HT, TT \}$)
- 그러나 1의 눈이 나올 때까지 주사위를 던진 횟수를 확률 변수 `X` 라 하면, `X` 가 취할 수 있는 모든 가능한 수는 무수히 많다.
- 이 경우에 확률 변수 `X` 의 상태 공간은 $S_{X} = \{ 1, 2, 3, \cdots \}$ 이고, 이 상태 공간을 이루는 숫자는 무수히 많으나 그 숫자들을 셈할 수 있다.
- 따라서 확률 변수 `X` 의 상태 공간을 구성하는 숫자는 유한개이거나 무수히 많더라도 셈할 수 있으며, 이러한 확률 변수를 이산 확률 변수라 한다.
이산 확률 변수(Discrete Random Variable)
확률 변수 `X` 에 대한 상태 공간을 구성하는 원소의 수가 유한개이거나 무수히 많더라도 셀 수 있는 경우에 `X` 를 이산 확률 변수(Discrete Random Variable)라 한다.
예제 : 주사위를 두 번 반복하여 던지는 시행에서 두 눈의 차의 절댓값을 확률 변수 `X` 라 한다. 이 때, `X` 의 상태 공간을 구하라.
주사위를 두 번 던지는 시행에서 첫 번째 나온 눈의 수를 `i`, 두 번째 나온 눈의 수를 `j` 라 하면 확률 변수 `X` 는 다음과 같이 정의된다.
| $$X = |i - j|, \; i, j = 1, 2, 3, 4, 5, 6$$ |
그러므로 `X` 의 상태 공간은 $S_{X} = \{0, 1, 2, 3, 4, 5 \}$ 이다.
예제 : 다음을 나타내는 확률 변수가 이산 확률 변수인지 아닌지 판단하라.
(a) 정류장에 도착한 버스에 승차한 승객의 수
(b) 새로 교체한 프로젝트용 전구의 수명
(a) 버스에 승차한 승객의 수는 셈을 할 수 있으므로 이산 확률 변수이다.
(b) 새로 교체한 프로젝트용 전구의 수명은 셈할 수 없으므로 이산 확률 변수가 아니다.
확률 질량 함수(Probability Mess Function)
`X` 의 상태 공간 $S_{X}$ 안에 있는 각각의 `x` 에 대해 $f(x) = P(X = x)$ 이고, $S_{X}$ 안에 있지 않은 모든 실수 `x` 에 대해 $f(x) = 0$ 으로 정의한 함수 $f(x)$, 즉 다음과 같이 정의되는 함수 `f(x)` 를 이산 확률 변수 `X` 의 확률 질량 함수(Probability Mess Function)라 한다.
$$f(x) = \begin{cases} P(X = x), & x \in S_{X} \\ 0, & x \not \in S_{X} \end{cases}$$
- 동전을 두 번 던지는 경우에 앞면이 나온 횟수를 확률 변수 `X` 라 하자.
- 그러면 `X` 의 상태 공간은 $S_{X} = \{ 0, 1, 2\}$ 이다. 그리고 앞면이 나온 횟수에 대한 사건과 확률 변수는 다음과 같다.
| $$\{ HH \} \; \Leftrightarrow \;X = 2, \quad \{ HT, TH \} \;\Leftrightarrow \;X = 1, \quad \{ TT \} \;\Leftrightarrow \;X = 0$$ |
- 특히, 각 사건에 대한 확률은 다음과 같다.
| $$P(\{HH\}) = \frac{1}{4}, \quad P(\{HT, TH\} = \frac{1}{2}, \quad P(\{TT\}) = \frac{1}{4}$$ |
- 따라서 다음과 같이 확률 변수 `X` 가 취하는 경우에 대한 확률을 정의할 수 있다.
- 즉, 확률 변수 `X` 에 대한 확률은 다음과 같다.
| $$P(X = 0) = \frac{1}{4}, \quad P(X=1) =\frac{1}{2}, \quad P(X=2) = \frac{1}{4}$$ |

- 위와 같이 표본 공간 안의 사건을 원소의 특성에 따라 확률 변수로 변환하면 확률 변수에 대한 확률을 정의할 수 있다.
- 이 때, 확률 변수 `X` 의 상태 공간 안에 있는 값 `x` 에 따라 확률이 변하므로 확률 변수 `X` 에 대한 확률을 나타내는 함수를 확률 질량 함수로 정의할 수 있다.
확률 질량 함수의 성질
- 확률 질량 함수 `f(x)` 는 다음 성질을 갖는다.
(1) 임의의 실수 `x` 에 대해 $0 ≤ f(x) ≤ 1$ 이다.
(2) $\displaystyle \sum_{\text{모든 x}} f(x) = 1$ 이다.
- 예를 들어, `X` 의 상태 공간이 $S_{X} = \{ x_{1}, x_{2}, x_{3}, \cdots, x_{n} \}$ 이고, $p_{i} = P(X = x_{i}), \; i = 1, 2, 3, \cdots, n$ 이면 다음의 확률표를 얻는다.
| `X` | $x_{1}$ | $x_{2}$ | $x_{3}$ | $\cdots$ | $x_{n}$ | 합계 |
| `f(x)` | $p_{1}$ | $p_{2}$ | $p_{3}$ | $\cdots$ | $p_{n}$ | 1 |
확률 분포(Probability Distribution)와 확률 히스토그램(Probability Histogram)
- 확률표와 같이 확률 변수 `X` 가 취할 수 있는 개개의 값에 확률을 대응시킨 것을 확률 변수 `X` 의 확률 분포(Probability Distribution)라 한다.
- 이와 같은 확률 분포는 위와 같이 확률표 또는 확률 질량 함수나 아래와 같이 확률 변수 `X` 가 취하는 값을 중심으로 밑변의 길이가 1이고 확률을 높이로 하는 확률 히스토그램(Probability Histogram)으로 나타낼 수 있다.
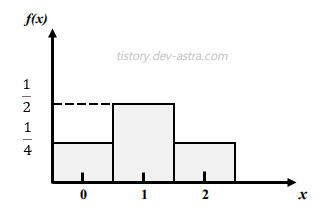
- 그러면 임의의 두 실수 `a` 와 `b` 에 대해 `X` 가 구간 $[a, b]$ 안에 들어갈 확률 $P(a ≤ X ≤ b)$ 는 다음과 같이 확률 질량 함수 `f(x)` 를 이용하여 구할 수 있다.
$$P(a ≤ X ≤ b) = \sum_{a ≤ x ≤ b} f(x)$$
- 특히, 정수값을 갖는 확률 변수 `X` 의 상태 공간 안에 있는 어떤 수 `a` 에 대해 다음을 얻는다.
$$P(X > a) = 1 - P(X ≤ a) \\ P(X ≥ a) = 1 - P(X ≤ a - 1)$$
예제 : 주사위를 두 번 반복하여 던지는 시행에서 두 눈의 차의 절댓값을 확률 변수 `X` 라 할 때, 다음을 구하라.
(a) 확률 변수 `X` 의 확률 질량 함수
(b) 두 눈의 차의 절댓값이 3일 확률
(c) 두 눈의 차의 절댓값이 2 이상 4 이하일 확률
(d) 두 눈의 차의 절댓값이 4 이상일 확률
(a)
확률 변수 `X` 가 취하는 각각의 수에 대한 사건을 나타내면 다음과 같다.
| $X = 0 \; \Leftrightarrow \; \{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) \} $ $X = 1 \; \Leftrightarrow \; \{ (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), (4, 3), (4, 5), (5, 4), (5, 6), (6, 5) \} $ $X = 2 \; \Leftrightarrow \; \{ (1, 3), (3, 1), (2, 4), (4, 2), (3, 5), (5, 3), (4, 6), (6, 4) \} $ $X = 3 \; \Leftrightarrow \; \{ (1, 4), (4, 1), (2, 5), (5, 3), (3, 6), (6, 3) \} $ $X = 4 \; \Leftrightarrow \; \{ (1, 5), (5, 1), (2, 6), (6, 2) \} $ $X = 5 \; \Leftrightarrow \; \{(1, 6), (6, 1) \} $ |
따라서 확률 변수 `X` 가 취하는 각각의 수에 대한 확률을 구하면 다음과 같다.
| $$P(X = 0) = \frac{6}{36}, P(X = 1) = \frac{10}{36}, P(X = 2) = \frac{8}{36}, P(X = 3) = \frac{6}{36}, P(X = 4) = \frac{4}{36}, P(X = 5) = \frac{5}{36} $$ |
그러면 `X` 의 확률 질량 함수는 다음과 같다.
| $$ \displaystyle f(x) = \begin{cases} \frac{1}{6}, & x = 0 \\ \frac{5}{18}, & x = 1 \\ \frac{2}{9}, & x = 2 \\ \frac{1}{6}, & x = 3 \\ \frac{1}{9}, & x = 4 \\ \frac{1}{18}, & x = 5 \\ 0, & \text{다른 곳에서} \end{cases}$$ |
(b)
두 눈의 차의 절댓값이 3일 확률은 $P(X = 3) = f(3) = \frac{1}{6}$ 이다.
(c)
두 눈의 차의 절댓값이 2 이상 4 이하일 확률은 다음과 같다.
| $$P(2 \le X \le 4) = f(2) + f(3) + f(4) = \frac{2}{9} + \frac{1}{6} + \frac{1}{9} = \frac{1}{2}$$ |
(d)
두 눈의 차의 절댓값이 4 이상일 확률은 다음과 같다.
| $$P(X \ge 4) = f(4) + f(5) = \frac{1}{9} + \frac{1}{18} = \frac{1}{6}$$ |
이산 확률 변수의 분포 함수(Distribution Function)
임의의 실수 `x` 에 대해 다음과 같이 정의되는 함수 `F(x)` 를 이산 확률 변수 `X` 의 분포 함수(Distribution Function)라 한다.
$$F(x) = P(X \le x) = \sum_{u \le x} f(u)$$
- 동전을 두 번 던져서 앞면이 나온 횟수 `X` 에 대해 확률 $\displaystyle P(X \le x) = \sum_{u \le x} f(u)$ 를 구해보자.
- 이를 위해 `X` 가 취하는 값 $\{ 0, 1, 2 \}$ 에 확률 `f(x)` 를 다음과 같이 표현할 수 있다.

- 그러면 위의 그림에서 보는 바와 같이 $P(X \le x)$ 의 값은 $x < 0, \; 0 \le x < 1, \; 1 \le x < 2, \; x \ge 2$ 에 따라 0이 아닌 `f(x)` 를 합한 확률이다.
- 따라서 임의의 실수 `x` 에 대해 확률 $P(X \le x)$ 는 다음과 같이 정의된다.
| $$\displaystyle f(x) = \begin{cases} 0, & x < 0 \\ \frac{1}{4}, & 0 \le x < 1 \\ \frac{3}{4}, & 1 \le x < 2 \\ 1, & x\ge 2 \end{cases}$$ |
- 즉, 이산 확률 변수 `X` 와 확률 질량 함수 `f(x)` 에 대해 확률 $P(X \le x)$ 를 분포 함수로 정의한다.
분포 함수와 확률
- 임의의 두 수 $a, b \; (a < b)$ 에 대해 분포 함수를 이용하여 다음과 같이 확률을 구할 수 있다.
$\bullet \; P(a < X \le b) = F(b) - F(a)$
$\eqalign{ \bullet \; P(a \le X \le b) &= F(b) - F(a) + P(X=a) \\ &= F(b) - F(\text{a 바로 전}) \\ &= F(b) - P(X < a)}$
$\eqalign{ \bullet \; P(X \ge a) &= 1 - F(a) + P(X=a) \\ &= 1 - P(X < a)}$
$\eqalign{ \bullet \; P(X=a) &= F(a) - F(a - 1) \\ &= F(a) - F(\text{a 바로 전}) \\ &= F(a) - P(X < a)}$
예제 : 주사위를 두 번 반복하여 던지는 시행에서 두 눈의 차의 절댓값을 확률 변수 `X` 라 할 때, 다음을 구하라.
(a) 확률 변수 `X` 의 분포 함수
(b) $P(X = 3)$
(c) $P(2 ≤ X ≤ 4)$
(d) $P(X \ge 4)$
확률 변수 `X` 가 취하는 각각의 수에 대한 사건을 나타내면 다음과 같다.
| $X = 0 \; \Leftrightarrow \; \{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) \} $ $X = 1 \; \Leftrightarrow \; \{ (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), (4, 3), (4, 5), (5, 4), (5, 6), (6, 5) \} $ $X = 2 \; \Leftrightarrow \; \{ (1, 3), (3, 1), (2, 4), (4, 2), (3, 5), (5, 3), (4, 6), (6, 4) \} $ $X = 3 \; \Leftrightarrow \; \{ (1, 4), (4, 1), (2, 5), (5, 3), (3, 6), (6, 3) \} $ $X = 4 \; \Leftrightarrow \; \{ (1, 5), (5, 1), (2, 6), (6, 2) \} $ $X = 5 \; \Leftrightarrow \; \{(1, 6), (6, 1) \} $ |
따라서 확률 변수 `X` 가 취하는 각각의 수에 대한 확률을 구하면 다음과 같다.
| $$P(X = 0) = \frac{6}{36}, P(X = 1) = \frac{10}{36}, P(X = 2) = \frac{8}{36}, P(X = 3) = \frac{6}{36}, P(X = 4) = \frac{4}{36}, P(X = 5) = \frac{5}{36} $$ |
그러면 `X` 의 확률 질량 함수는 다음과 같다.
| $$ \displaystyle f(x) = \begin{cases} \frac{1}{6}, & x = 0 \\ \frac{5}{18}, & x = 1 \\ \frac{2}{9}, & x = 2 \\ \frac{1}{6}, & x = 3 \\ \frac{1}{9}, & x = 4 \\ \frac{1}{18}, & x = 5 \\ 0, & \text{다른 곳에서} \end{cases}$$ |
(a)
확률 변수 `X` 가 취하는 값 `0, 1, 2, 3, 4, 5` 를 경계로 0이 아닌 `f(x)` 를 더하면 다음을 얻는다. (분포 함수)
| $$ \displaystyle F(x) = \begin{cases} 0, & x < 0 \\ \frac{6}{36}, & 0 \le x < 1 \\ \frac{16}{36}, & 1 \le x < 2 \\ \frac{24}{36}, & 2 \le x < 3 \\ \frac{30}{36}, & 3 \le x < 4 \\ \frac{34}{36}, & 4 \le x < 5 \\ 1, & x \ge 5 \end{cases}$$ |
(b)
$\displaystyle P(X = 3) = F(3) - F(2) = \frac{30}{36} - \frac{24}{36} = \frac{6}{36} = \frac{1}{6}$
(c)
$\displaystyle P(2 \le X \le 4) = F(4) - F(2) + P(X = 2) = \frac{34}{36} - \frac{24}{36} + \frac{8}{36} = \frac{18}{36} = \frac{1}{2}$
(d)
$\displaystyle P(X \ge 4) = 1 - P(X \le 3) = 1 - F(3) = 1 - \frac{30}{36} = \frac{6}{36} = \frac{1}{6}$
분포 함수의 그래프
- 한편, 동전을 두 번 던져서 나온 앞면의 횟수 `X` 에 대한 분포 함수 `F(x)` 의 그래프는 다음과 같다.

- 이 때, 분포 함수 `F(x)` 는 이산 확률 변수 `X` 가 취하는 값 `0, 1, 2` 에서 불연속이다.
- 그리고 `F(x)` 가 불연속인 각 점에서 함수의 차이가 `0.25, 0.5, 0.25` 이며, 이는 `X` 가 취하는 값 `0, 1, 2` 에 대한 확률인 것을 알 수 있다.
- 따라서 이산 확률 변수 `X` 의 분포 함수 `F(x)` 를 알고 있다면, 확률 질량 함수 `f(x)` 를 구할 수 있다.
예제 : 다음 분포 함수를 갖는 이산 확률 변수 `X` 의 확률 질량 함수를 구하라.
| $$F(x) = \begin{cases} 0, & x < 1 \\ \frac{1}{2}, & 1 \le x < 3 \\ \frac{2}{3}, & 3 \le x < 5 \\ 1, & x \ge 5 \end{cases}$$ |
분포 함수 `F(x)` 가 `x = 1, 3, 5` 에서 불연속이고, 각 점에서 함수의 차이는 각각 $\displaystyle \frac{1}{2}, \; \frac{2}{3} - \frac{1}{2} = \frac{1}{6}, \; 1 - \frac{2}{3} = \frac{1}{3}$ 이므로 `X` 의 확률 질량 함수는 다음과 같다.
| $$f(x) = \begin{cases} \frac{1}{2}, & x = 1 \\ \frac{1}{6}, & x = 3 \\ \frac{1}{3}, & x =5 \\ 0, & \text{다른 곳에서} \end{cases}$$ |
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
|---|---|
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |
| [확률과 통계] 베이즈 정리 (0) | 2022.10.31 |
| [확률과 통계] 조건부 확률 (0) | 2022.10.31 |
| [확률과 통계] 확률 (0) | 2022.10.31 |
| [확률과 통계] 시행과 사건 (0) | 2022.10.31 |
