연속 확률 분포
- 종 모양의 대칭형인 연속 확률 분포를 정규 분포라 한다.
정규 분포(Normal Distribution)
연속 확률 변수 `X` 의 확률 밀도 함수 `f(x)` 가 다음과 같을 때, 확률 변수 `X` 는 모수 `μ` 와 $σ^{2}$ 인 정규 분포(Normal Distribution)를 따른다 하고, $X \sim N(μ, σ^{2})$ 으로 나타낸다.
$$f(x) = \frac{1}{\sqrt{2π}σ}e^{-\frac{(x - μ)^{2}}{2σ^{2}}}, \quad -\infty < x < \infty$$
- 자연 현상이나 사회 현상에서 얻게 되는 대부분의 자료에 대한 히스토그램은 자료의 수가 클수록 계급 간격이 좁아지고, 아래와 같이 좌우 대칭인 종 모양의 곡선에 가까워진다.
- 또한 이항 분포 $B(n, p)$ 에서 `p` 가 일정하고 `n` 이 커지면 이항 분포의 그래프는 종 모양에 가까워진다.
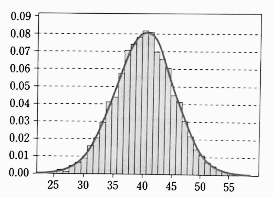
확률 밀도 함수와 특징
- 어떤 연속 확률 변수 `X` 는 다음과 같은 확률 밀도 함수를 갖는다.
$$f(x) = \frac{1}{\sqrt{2π}σ}e^{-\frac{(x - μ)^{2}}{2σ^{2}}}, \quad -\infty < x < \infty$$
- 이 때, 이 확률 밀도 함수 `f(x)` 는 다음의 성질을 갖는다.
| (1) `x = μ` 에 관해 좌우 대칭이다. (2) `x = μ` 에서 최댓값을 갖는다. (3) `x = μ ± σ` 에서 곡선의 모양이 위로 볼록하다가 아래로 볼록하게 바뀐다. (변곡점을 갖는다.) (4) `x = μ ± 3σ` 에서 `x` 축에 거의 접하는 모양을 가지고, $x \rightarrow ± \infty$ 이면 $f(x) \rightarrow 0$ 이다. |

- 이와 같이 연속 확률 변수의 분포가 종 모양인 확률 분포를 정규 분포라고 한다.
중앙값과 최빈값
- 모수 `μ` 와 $σ^{2}$ 은 각각 확률 변수 `X` 의 평균과 분산이다.
- 특히 확률 밀도 함수 $f(x)$ 의 성질로부터 정규 분포의 중앙값과 최빈값에 대한 정보를 얻을 수 있다.
| (1) `x = μ` 에 관해 좌우 대칭이므로, `X` 의 중위수는 $M_{e} = m$ 이다. (2) `x = μ` 에서 최댓값을 가지므로, `X` 의 최빈값은 $M_{o} = m$ 이다. |
- 정규 분포는 평균이 다르고 분산이 동일하면, 중심 위치만 다르고 동일한 모양을 이룬다.
- 그리고 분산이 클수록 평균을 중심으로 폭넓게 분포한다.

표준 정규 분포(Standard Normal Distribution)
평균 $μ = 0$, 분산 $σ^{2} = 1$ 인 정규 분포를 표준 정규 분포(Standard Normal Distribution)라고 하고, $Z \sim N(0, 1)$ 로 나타낸다.
확률 밀도 함수와 특징
- 표준 정규 분포에 따르는 확률 변수 `Z` 의 확률 밀도 함수 $\phi(z)$ 는 다음과 같다.
$$\phi(x) = \frac{1}{\sqrt{2π}}e^{-\frac{z^{2}}{2}}, \quad -\infty < z < \infty$$
- 그러므로 표준 정규 분포 곡선은 다음 성질을 갖는다.
| (1) `z = 0` 에 관해 좌우 대칭이고, `Z` 의 중앙값은 $M_{e} = 0$ 이다. (2) `z = 0` 에서 최댓값을 가지며, `Z` 의 최빈값은 $M_{o} = 0$ 이다. (3) `z = ± 1` 에서 $\phi(z)$ 는 변곡점을 갖는다. (4) `z = ± 3` 에서 `z` 축에 거의 접하는 모양을 가지고, $z \rightarrow ± \infty$ 이면 $\phi(z) \rightarrow 0$ 이다. |
예제 : 다음 정규 분포에 대해 물음에 답하라.
| $$N(1, 4), \; N(-1, 9), \; N(2, 1), \; N(8, 16)$$ |
(a) 각 정규 분포에 대한 평균과 표준 편차를 구하라.
(b) 분포 모양이 가장 밀집된 분포와 가장 왼쪽에 있는 분포를 구하라.
(a)
$N(1, 4)$ 의 평균은 $μ = 1$, 표준 편차는 $σ = \sqrt{4} = 2$ 이다.
$N(-1, 9)$ 의 평균은 $μ = -1$, 표준 편차는 $σ = \sqrt{9} = 3$ 이다.
$N(2, 1)$ 의 평균은 $μ = 2$, 표준 편차는 $σ = \sqrt{1} = 1$ 이다.
$N(8, 16)$ 의 평균은 $μ = 8$, 표준 편차는 $σ = \sqrt{16} = 4$ 이다.
(b)
가장 밀집된 분포는 표준 편차가 가장 작은 $N(2, 1)$ 이다.
가장 왼쪽에 있는 분포는 평균이 가장 작은 $N(-1, 9)$ 이다.
표준 정규 분포의 성질
- 표준 정규 분포의 대칭성을 이용하면 양수 `z` 에 대해 표준 정규 분포는 다음 성질을 갖는다.
| (1) $P(Z \le 0) = P(Z \ge 0) = 0.5$ (2) $P(Z \le -z) = P(Z \ge z)$ (3) $P(0 \le Z \le z) = P(Z \le z) - 0.5$ (4) $P(Z \ge z) = 0.5 - P(0 \le Z \le z)$ (5) $P(-z \le Z \le 0) = P(0 \le Z \le z)$ (6) $P(-z \le Z \le z) = 2P(0 \le Z \le z) = 2P(Z \le z) - 1$ |
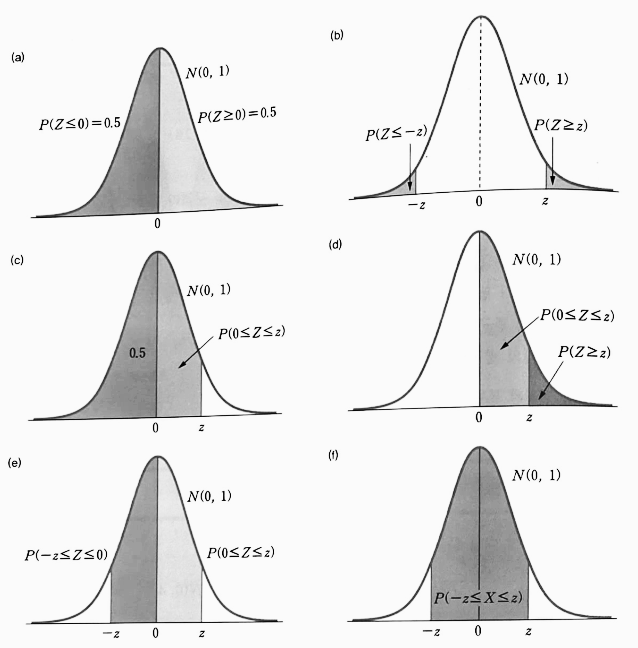
- `z > 0` 에 대해 확률 $P(Z \le -z)$ 와 $P(Z \ge z)$ 를 꼬리 확률(Tail Probability)이라 한다.
- 아래와 같이 오른쪽 꼬리 확률이 `α` 인 $100(1 - α)%$ 백분위수를 $z_{α}$ 로 표시하면 다음을 얻는다.
$$P(Z \le z_{α}) = 1 - α, \; P(Z \ge z_{α}) = α$$

- 특히, 오른쪽 꼬리 확률이 $α = 0.05, 0.025, 0.005$ 인 백분위수 $z_{α}$ 는 각각 다음과 같다.
| $$P(Z > 1.645) = 0.05, \; P(Z > 1.96) = 0.025, \; P(Z > 2.58) = 0.005$$ |
- 즉, $z_{0.05} = 1.645, \; z_{0.025} = 1.96, \; z_{0.005} = 2.58$ 이다.
- 그리고 다음과 같이 양쪽 꼬리 확률이 각각 $\frac{α}{2} = 0.05, 0.025, 0.005$ 가 되는 `α` 에 대한 중심 확률 $P(|Z| < z_{\frac{α}{2}}$) 는 각각 다음과 같다.
| $$P(|Z| < 1.645) = 0.9, \; P(|Z| < 1.96) = 0.95, \; P(|Z| < 2.58) = 0.99$$ |

정규 분포의 확률 계산 (표준 정규 분포표 이용)
- 일반적으로 표준 정규 분포의 확률 밀도 함수 $\phi(z)$ 를 구간 $[a, b]$ 에서 적분하는 것은 불가능하다.
- 그러나 이항 분포와 같이 표준 정규 분포표를 이용하여 확률 $P(Z \le a)$ 를 구할 수 있다.
- 예를 들어, $P(Z \le 1.04)$ 는 표준 정규 분포표를 이용하여 다음과 같이 구한다.
| ① `z` 열에서 소수점 첫째 자리 숫자 `1.0` 을 선택한다. ② `z` 행에서 소수점 둘째 자리 숫자 `0.04` 를 선택한다. ③ `z` 열이 `1.0` 인 행과 `z` 행이 `0.04` 인 열이 만나는 위치의 수 `0.8508` 을 선택한다. ④ $P(Z \le 1.04) = 0.8508$ 이다. |

표준 정규 분포표(Standard Normal Distribution Table)
- 따라서 표준 정규 확률 변수 `Z` 에 대해 $P(a \le Z \le b)$ 는 다음과 같이 구할 수 있다.
$$P(a \le Z \le b) = P(Z \le b) - P(Z \le a)$$
- 예를 들어, $P(0.95 \le Z \le 1.43)$ 은 먼저 표준 정규 분포표를 이용하여 $P(Z \le 1.43) = 0.9236$ 과 $P(Z \le 0.95) = 0.8289$ 를 구한다.
- 그러면 구하고자 하는 확률은 다음과 같다.
| $$P(0.95 \le Z \le 1.43) = P(Z \le 1.43) - P(Z \le 0.95) = 0.9236 - 0.8289 = 0.0947$$ |
정규 분포와 표준 정규 분포의 관계
- 평균이 `μ` 이고 표준 편차가 `σ` 인 임의의 확률 변수 `X` 를 $\displaystyle Z = \frac{X - μ}{σ}$ 로 표준화하면 $E(Z) = 0, \; \text{Var}(Z) = 1$ 임을 살펴 보았다. (관련 내용 바로가기)
- 특히 정규 분포 $N(μ, σ^{2})$ 에 따르는 확률 변수 `X` 의 표준화 확률 변수 `Z` 는 표준 정규 분포를 따른다.
- 즉, 정규 분포 $X \sim N(μ, σ^{2})$ 와 표준 정규 분포 $Z \sim N(0, 1)$ 사이에 다음 관계가 성립한다.
$$X \sim N(μ, \; σ^{2}) \quad \Leftrightarrow \quad Z = \frac{X - μ}{σ} \sim N(0, \; 1)$$
- 따라서 일반적인 정규 분포의 확률은 다음과 같이 표준 정규 분포를 이용하여 구할 수 있다.
$$P(a \le X \le b) = P(\frac{a - μ}{σ} \le Z \le \frac{b - μ}{σ})$$
예
- 정규 분포 $N(30, 16)$ 을 따르는 확률 변수 `X` 에 대해 $P(27 \le X \le 35)$ 를 구한다면, $μ = 30, \; σ = 4$ 이므로 `X` 를 다음과 같이 표준화한다.
| $$\frac{27-30}{4} \le \frac{X - 30}{4} \le \frac{35 - 30}{4} \quad \Rightarrow \quad -0.75 \le Z \le 1.25$$ |
- 그러면 확률 $P(27 \le X \le 35)$ 는 다음과 같이 구할 수 있다.
| $$\eqalign{ P(27 \le X \le 35) & = P(-0.75 \le Z \le 1.25) = P(Z \le 1.25) - P(Z \le -0.75) \\ &= P(Z \le 1.25) - P(Z \ge 0.75) \\ & = P(Z \le 1.25) - [1 - P(Z \le 0.75)] \\ & = 0.8944 - (1 - 0.7734) = 0.6678}$$ |
정규 분포의 합성
- 두 확률 변수 `X` 와 `Y` 가 독립이고, $X \sim N(μ_{1}, \; σ_{1}^{2}), \; Y \sim N(μ_{2}, \; σ_{2}^{2})$ 일 때, 두 확률 변수의 합 $X + Y$ 와 차 $X - Y$ 는 다음과 같은 정규 분포를 따르는 것으로 알려져 있다.
$$X + Y \sim N(μ_{1} + μ_{2}, \; σ_{1}^{2} + σ_{2}^{2}) \\ X - Y \sim N(μ_{1} - μ_{2}, \; σ_{1}^{2} - σ_{2}^{2}) $$
이항 분포의 정규 근사
이항 분포와 정규 분포의 관계
확률 변수 `X` 가 이항 분포 $B(n, \; p)$ 를 따를 때, `n` 이 충분히 크면 `X` 는 정규 분포 $N(np, \; npq)$ 에 근사한다. (단, $q = 1 - p$ 이다.)
- 이항 분포 $B(n, \; p)$ 에서 `p` 가 일정하고 `n` 이 커지면 이항 분포의 그래프는 종 모양에 가까워지는 것을 살펴 보았다. (관련 내용 바로가기)
- 그리고 정규 분포의 그래프는 종 모양을 이루는 것을 알고 있다.
- 따라서 이항 분포 $B(n, \; p)$ 에서 `p` 가 일정하고 `n` 이 충분히 커지면 이항 분포는 정규 분포에 가까워지는 것을 알 수 있다.
- 일반적으로 $np \ge 5, \; nq \ge 5$ 일 때, 이항 분포는 평균 $μ = np$, 분산 $σ^{2} = npq$ 인 정규 분포 $N(np, \; npq)$ 에 가까워지며, 이를 이항 분포의 정규 근사(Normal Approximation)라 한다.
- 따라서 확률 변수 `X` 가 이항 분포 $B(n, \; p)$ 를 따를 때 `n` 이 충분히 크면 표준화 확률 변수 `Z` 는 표준 정규 분포에 가까워진다. 즉, 다음이 성립한다.
$$X \sim B(n, \; p) \buildrel {\quad n \rightarrow \infty \quad } \over \longrightarrow Z = \frac{X - np}{\sqrt{npq}} \approx N(0, \; 1)$$
예제 : 5지선다형인 100문제를 무작위로 선정하여 정답을 14개 이상 25개 이하로 맞출 근사 확률을 구하라.
5지선다형인 100문제를 무작위로 답안을 선정하여 정답을 맞춘 개수를 확률 변수 `X` 라 하면, $X \sim B(100, \frac{1}{5})$ 이다. 따라서 `X` 의 평균과 분산을 구하면 각각 다음과 같다.
| $$μ = 100 \times \frac{1}{5} = 20, \quad σ^{2} = 100 \times \frac{1}{5} \times \frac{4}{5} = 16$$ |
따라서 확률 변수 `X` 는 근사적으로 정규 분포 $N(20, 16)$ 을 따른다.
그러므로 구하고자 하는 근사 확률은 다음과 같다.
$\eqalign { P(14 \le X \le 25) & \approx P(\frac{14 - 20}{4} \le \frac{X - 20}{4} \le \frac{25 - 20}{4}) \\ & = P(-1.5 \le Z \le 1.25) = P(Z \le 1.25) - P(Z \le -1.5) \\ & = P(Z \le 1.25) - [1 - P(Z \le 1.5)] \\ &= 0.8944 - (1 - 0.9332) = 0.8276}$
연속성 수정 정규 근사(Normal Approximation with Continuity Correction Factor)
- 위의 예제에서 본 것과 같이, $X \sim B(100, \frac{1}{5})$ 일 때, 이항 분포의 정규 근사에 의해 확률 변수 `X` 가 14 이상 25 이하일 근사 확률을 구하면 $P(14 \le X \le 25) = 0.8276$ 이다.
- 그러나 컴퓨터를 이용하여, 이 확률을 구하면 $P(14 \le X \le 25) = 0.8656$ 이다.
- 따라서 0.038의 오차가 발생하지만, 다음과 같이 근사 확률을 구하면 이항 분포에 의한 확률과 비교하여 오차가 0.0023으로 더욱 줄어든다.
| $\eqalign { P(13.5 \le X \le 25.5) & \approx P(\frac{13.5 - 20}{4} \le \frac{X - 20}{4} \le \frac{25.5 - 20}{4}) \\ & = P(-1.625 \le Z \le 1.375) = P(Z \le 1.375) - P(Z \le -1.625) \\ & = P(Z \le 1.375) - [1 - P(Z \le 1.625)] \\ &= 0.9154 - (1 - 0.9479) = 0.8633}$ |
- 이러한 사실은 이항 분포에 대한 확률 히스토그램을 그리면 명확해진다.

- (a)에 보인 이항 분포 $B(100, \frac{1}{5})$ 의 확률 히스토그램은 확률 변수가 취하는 값 `x` 를 중심으로 밑변의 길이가 1이고 확률 $P(X = x)$ 가 높이인 직사각형들로 이루어진다.
- 따라서 이항 분포에서 확률 $P(14 \le X \le 25)$ 는 `13.5` 부터 `25.5` 까지 밑변의 길이가 1인 직사각형들의 넓이의 합이다.
- 그러나 이항 분포의 정규 근사에 의한 확률은 (b)와 같이 $14 \le x \le 25$ 범위에서 정규 곡선으로 둘러싸인 부분의 넓이이다.
- 따라서 다음과 같이 $13.5 \le x \le 14$ 와 $25 \le x \le 25.5$ 사이의 넓이를 고려해야 한다.
- 즉, 정규 분포에서 $13.5 \le x \le 25.5$ 인 구간에서 정규 곡선으로 둘러싸인 부분의 넓이인 확률 $P(13.5 \le X \le 25.5)$ 를 구한다.

- 이와 같은 방법에 의해 구한 근사 확률을 연속성 수정 정규 근사(Normal Approximation with Continuity Connection Factor)라 한다.
연속성 수정 정규 근사에 의한 근사 확률 계산
- 시행 횟수 `n` 이 충분히 큰 이항 분포 $B(n, \; p)$ 에서 확률 $P(a \le X \le b)$ 를 구하기 위해 정규 분포 $N(np, \; npq)$ 를 이용한다면, 다음과 같이 연속성 수정 정규 근사에 의한 근사 확률을 구할 수 있다.
- 이 때, `a` 와 `b` 는 정수이다.
① $\displaystyle P(X \le b) \approx P(Z \le \frac{b + 0.5 - μ}{σ})$
② $\displaystyle P(a \le X) \approx 1 - P(Z \le \frac{a - 0.5 - μ}{σ})$
③ $\displaystyle P(a \le X \le b) \approx P(Z \le \frac{b + 0.5 - μ}{σ}) - P (Z \le \frac{a - 0.5 - μ}{σ})$
④ $\displaystyle P(X = a) \approx P(Z \le \frac{a + 0.5 - μ}{σ}) - P(Z \le \frac{a - 0.5 - μ}{σ})$
예제 : 확률 변수 `X` 가 `B(100, 0.4)` 를 따를 때, 정규 분포를 이용하여 다음 근사 확률을 구하라.
(a) $P(X \le 47)$
(b) $P(X \ge 34)$
(c) $P(X = 43)$
(d) $P(35 \le X \le 45)$
$X \sim B(100, 0.4)$ 이므로 `X` 의 평균과 분산, 표준 편차를 구하면 각각 다음과 같다.
| $$μ = 100 \times 0.4 = 40, \quad σ^{2} = 100 \times 0.4 \times 0.6 = 24, \quad σ = \sqrt{24} ≒ 4.9$$ |
따라서 확률 변수 `X` 는 근사적으로 정규 분포 $N(40, 4.9^{2})$ 을 따른다.
(a)
$\displaystyle P(X \le 47) = P(X \le 47.5) \approx P(Z \le \frac{47.5 - 40}{4.9} = P(Z \le 1.53) = 0.9370$
(b)
$\displaystyle P(X \ge 34) = P(X \ge 33.5) \approx P(Z \le \frac{33.5 - 40}{4.9} = P(Z \ge -1.33) = P(Z \le 1.33) = 0.9066$
(c)
$\displaystyle \eqalign { P(X = 43) = P(42.5 \le X \le 43.5) & \approx P(\frac{42.5 - 40}{4.9} \le Z \le \frac{43.5 - 40}{4.9}) \\ & = P(0.51 \le Z \le 0.71) = P(Z \le 0.71) - P(Z \le 0.51) \\ & = 0.7611 - 0.6950 = 0.0661 }$
(d)
$\displaystyle \eqalign { P(35 \le X \le 45) = P(34.5 \le X \le 45.5) & \approx P(\frac{34.5 - 40}{4.9} \le Z \le \frac{45.5 - 40}{4.9}) \\ & = P(-1.12 \le Z \le 1.12) = 2P(Z \le 1.12) - 1 \\ & = 2 \times 0.8686 - 1 = 0.7372 }$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 통계적 가설 검정 (0) | 2022.11.28 |
|---|---|
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |
| [확률과 통계] 이산 확률 변수 (0) | 2022.11.07 |
