728x90
728x90
베이즈 정리
- 확률이 0이 아닌 사건들 $A_{1}, A_{2}, \cdots, A_{n}$ 이 어떤 사건 `B` 의 발생에 원인이 된다고 하자.
- 이 때, 주어진 사건 $A_{i}, \; i = 1, 2, \cdots, n$ 의 조건부 확률을 이용하여 사건 `B` 가 발생할 확률을 구할 수 있다.
- 또한 사건 `B` 가 발생했을 때, 사건 `B` 의 발생 요인들 중에서 어느 특정한 요인이 작용할 확률을 구할 수 있다.
전확률 공식(Formula of Total Probability)
확률이 0이 아닌 사건 $A_{1}, A_{2}, \cdots, A_{n}$ 을 표본 공간 `S` 의 분할이라 하면, 임의의 사건 `B` 의 확률은 다음과 같다.
$$P(B) = \sum_{i=1}^{n}P(A_{i})P(B|A_{i})$$
증명
- 확률이 0이 아닌 사건들 $A_{1}, A_{2}, \cdots, A_{n}$ 이 표본 공간 `S` 의 분할이라 하면, 다음을 만족한다.
- $A_{i} ∩ A_{j} = \varnothing, \; \; i ≠ j, \; \; i, j = 1, 2, \cdots, n$
- $S = A_{1} ∪ A_{2} ∪ \cdots ∪ A_{n}$
- 이 때, 임의의 사건을 `B` 라 하면 아래와 같이 사건 `B` 를 쌍마다 배반인 사건 $B ∩ A_{1}, B ∩ A_{2}, \cdots, B ∩ A_{n}$ 으로 분할할 수 있다.
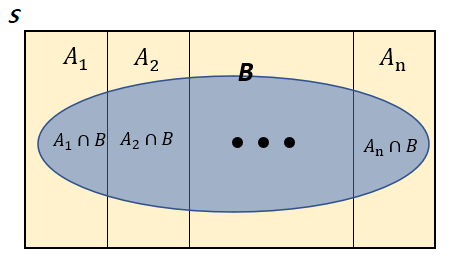
- 따라서 사건 `B` 의 확률은 다음과 같이 분할된 사건의 확률을 합한 것과 같다.
| $$P(B) = P(B ∩ A_{1}) + P(B ∩ A_{2}) + \cdots + P(B ∩ A_{n})$$ |
- 한편, 곱의 법칙을 이용하여 분할 사건 $B ∩ A_{i}, \; \; i = 1, 2, \cdots, n$ 의 확률을 구하면 다음과 같다.
| $$B ∩ A_{i} = P(A_{i})P(B|A_{i})$$ |
- 그러면 사건 `B` 의 확률을 다음과 같이 구할 수 있다.
| $$P(B) = \sum_{i=1}^{n}P(A_{i})P(B|A_{i})$$ |
예제 : 의학 보고서에 따르면 전체 국민의 7%가 폐질환을 앓고 있으며, 그들 중 85%가 흡연가라고 한다. 그리고 폐질환을 갖지 않은 사람 중에 25%가 흡연가라 한다. 임의로 선정한 사람이 흡연가일 확률을 구하라.
더보기
폐질환을 앓고 있는 사람을 `A` 라 하면 `P(A) = 0.07` 이므로, 여사건의 확률은 $P(A^{C}) = 0.93$ 이다.
임의로 선정한 사람이 흡연가일 사건을 `B` 라 하면 `P(B|A) = 0.85`, $P(B|A^{C}) = 0.25$ 이다.
따라서 임의로 선정한 사람이 흡연가일 확률은 다음과 같다.
$$P(B) = P(A)P(B|A) + P(A^{C})P(B|A^{C}) = 0.07 \times 0.85 + 0.93 \times 0.25 = 0.292$$
베이즈 정리(Bayes' Theorem)
사건 $A_{1}, A_{2}, \cdots, A_{n}$ 이 표본 공간 `S` 의 분할이라 하고 $P(B) > 0$ 인 어떤 사건 `B` 가 발생했을 때, 사건 `A_{i}` 의 조건부 확률은 다음과 같다.
$$P(A_{i} | B) = \frac{P(A_{i})P(B|A_{i})}{\sum\limits_{j=1}^{n}P(A_{j})P(B|A_{j})}$$
증명
- 확률이 0이 아닌 사건 $A_{1}, A_{2}, \cdots, A_{n}$ 을 표본 공간 `S` 의 분할이라 하고, 사건 `B` 의 확률이 0이 아니라고 하자.
- 이 때, 사건 `B` 가 주어졌다는 조건 아래서 사건 `A_{i}` 의 조건부 확률 $P(A_{i}|B)$ 는 다음과 같다.
| $$P(A_{i} | B) = \frac{P(A_{i} ∩ B)}{P(B)}$$ |
- 곱의 법칙과 전확률 공식을 이용하면 다음을 얻을 수 있다.
| $$P(A_{i} ∩ B) = P(A_{i})P(B | A_{j}) \\ P(B) = \sum\limits_{j=1}^{n}P(A_{j})P(B|A_{j})$$ |
- 따라서 사건 `B` 가 주어졌다고 할 때, 조건부 확률 $P(A_{i}|B)$ 는 다음과 같이 구할 수 있다.
| $$P(A_{i} | B) = \frac{P(A_{i}∩B)}{P(B)} = \frac{P(A_{i})P(B|A_{i})}{\sum\limits_{j=1}^{n}P(A_{j})P(B|A_{j})}$$ |
사전 확률(Prior Probability)과 사후 확률(Posterior Probability)
- 사건 `B` 의 발생 원인을 제공하는 확률 $P(A_{i})$ 를 사전 확률(Prior Probability)이라 하고, 사건 `B` 가 발생한 이후의 확률 $P(A_{i} | B)$ 를 사후 확률(Poserior Probability)이라 한다.
예제 : 의학 보고서에 따르면 전체 국민의 7%가 폐질환을 앓고 있으며, 그들 중 85%가 흡연가라고 한다. 그리고 폐질환을 갖지 않은 사람 중에 25%가 흡연가라 한다. 임의로 선정한 사람이 흡연가라고 할 때, 이 사람이 폐질환을 앓고 있을 확률을 구하라.
더보기
흡연가가 선정되었을 때, 이 사람이 페질환을 앓고 있을 확률은 다음과 같다.
$$P(A|B) = \frac{P(A)P(B|A)}{P(B)} = \frac{0.07 \times 0.85}{0.292} = \frac{0.0595}{0.292} = 0.2038$$
728x90
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
|---|---|
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |
| [확률과 통계] 이산 확률 변수 (0) | 2022.11.07 |
| [확률과 통계] 조건부 확률 (0) | 2022.10.31 |
| [확률과 통계] 확률 (0) | 2022.10.31 |
| [확률과 통계] 시행과 사건 (0) | 2022.10.31 |
| [확률과 통계] 도수 분포표에서의 평균과 분산 (1) | 2022.10.11 |
