행렬식
- 하나 이상의 수로 구성된 `n` 차 정사각 행렬에는 이 행렬을 대표하는 수를 대응할 수 있는데, 그 수를 구하는 식을 행렬식(Determinant)이라고 한다.
- 행렬식을 이용하면 역행렬이 존재하는지 여부를 판별할 수 있고, 연립 일차 방정식의 해가 유일하게 존재하는지도 판단할 수 있다.
행렬식(Determinant : $det(A)$ 또는 $|A|$)
`n` 차 정사각 행렬에 대응하는 수를 구하는 식
$$det(A) = |A| = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} $$
2차, 3차 정사각 행렬의 기본 행렬식
① 2차 정사각 행렬 $A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$ 의 행렬식
$$det(A) = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{12}a_{21} $$
② 3차 정사각 행렬 $B = \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix}$ 의 행렬식
$$def(B) = \begin{vmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{vmatrix} = (b_{11}b_{22}b_{33} + b_{12}b_{23}b_{31} + b_{13}b_{21}b_{32}) - (b_{13}b_{22}b_{31} + b_{11}b_{23}b_{32} + b_{12}b_{21}b_{33})$$
- 위에서 정의한 행렬식은 기본 행렬식으로, 2차 또는 3차 정사각 행렬에서만 사용할 수 있다.
- 기본 행렬식은 다음과 같이 행렬의 연두색 선 방향에 있는 원소들을 곱한 후 더한 값에서 주황색 선 방향의 원소들을 곱한 후 더한 값을 빼는 방식으로 행렬을 대표하는 값을 구한다.

예제 : 3차 정사각행렬 $A = \begin{bmatrix} 3 & 0 & 1 \\ -4 & 2 & 1 \\ 5 & -3 & 5 \end{bmatrix}$ 의 행렬식을 구하시오.
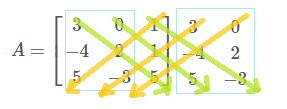
$det(A) = \{ 3 × 2 × 5 + 0 × 1 × 5 + 1 × (-4) × (-3) \} - \{ 1 × 2 × 5 + 3 × 1 × (-3) + 0 × (-4) × 5 \} = 41$
3차 이상인 정사각 행렬의 행렬식
- 여인수(Cofactor)의 개념을 이용하여 행렬식을 구할 수 있다.
- 3차 정사각 행렬의 경우, 기본 행렬식뿐 아니라 여인수를 이용해서도 행렬식을 구할 수 있다.
- 4차 이상의 정사각 행렬에 대해서는 기본 행렬식의 공식을 바로 적용할 수 없고, 여인수의 개념을 이용해야 행렬식을 구할 수 있다.
- 여인수는 행렬의 소행렬을 이용하여 구할 수 있다.
소행렬(Minor Matrix : $M_{ij}$ )
`n` 차 정사각 행렬에서 `i` 행과 `j` 열을 제거해서 얻은 `(n - 1) × (n - 1)` 행렬
예 : 행렬 $A = \begin{bmatrix} 11 & 12 & 13 & 14 \\ 21 & 22 & 23 & 24 \\ 31 & 32 & 33 & 34 \\ 41 & 42 & 43 & 44 \end{bmatrix}$
- 소행렬 $M_{11}$ 을 구한다면, 행렬 `A` 에서 1행과 1열을 제외한 나머지 부분으로 구할 수 있다.
| $A = \begin{bmatrix} 11 & 12 & 13 & 14 \\ 21 & 22 & 23 & 24 \\ 31 & 32 & 33 & 34 \\ 41 & 42 & 43 & 44 \end{bmatrix} \quad \Rightarrow \quad M_{11} = \begin{bmatrix} 22 & 23 & 24 \\ 32 & 33 & 34 \\ 42 & 43 & 44 \end{bmatrix}$ |
- 소행렬 $M_{32}$ 을 구한다면, 행렬 `A` 에서 3행과 2열을 제외한 나머지 부분으로 구할 수 있다.
| $A = \begin{bmatrix} 11 & 12 & 13 & 14 \\ 21 & 22 & 23 & 24 \\ 31 & 32 & 33 & 34 \\ 41 & 42 & 43 & 44 \end{bmatrix} \quad \Rightarrow \quad M_{32} = \begin{bmatrix} 11 & 13 & 14 \\ 21 & 23 & 24 \\ 41 & 43 & 44 \end{bmatrix}$ |
소행렬식(Minor Determinant : $det(M_{ij})$)
`n` 차 정사각 행렬의 소행렬 $M_{ij}$ 의 행렬식
예 : 행렬 $A = \begin{bmatrix} 11 & 12 & 13 & 14 \\ 21 & 22 & 23 & 24 \\ 31 & 32 & 33 & 34 \\ 41 & 42 & 43 & 44 \end{bmatrix}$
| $M_{11} = \begin{bmatrix} 22 & 23 & 24 \\ 32 & 33 & 34 \\ 42 & 43 & 44 \end{bmatrix}, \quad M_{43} = \begin{bmatrix} 11 & 12 & 14 \\ 21 & 22 & 24 \\ 31 & 32 & 34 \end{bmatrix}$ |
- 2차 또는 3차 정사각 행렬인 경우에는 기본 행렬식을 이용하여 구할 수 있다.
| $det(M_{11}) = \begin{vmatrix} 22 & 23 & 24 \\ 32 & 33 & 34 \\ 42 & 43 & 44 \end{vmatrix} = (22 × 33 × 44 + 23 × 34 × 42 + 24 × 32 × 43) - (24 × 33 × 42 + 22 × 34 × 43 + 23 × 32 × 44)$ $det(M_{43}) = \begin{vmatrix} 11 & 12 & 14 \\ 21 & 22 & 24 \\ 31 & 32 & 34 \end{vmatrix} = (11 × 22 × 34 + 12 × 24 × 31 + 14 × 21 × 32) - (14 × 22 × 31 + 12 × 21 × 34 + 11 × 24 × 32) $ |
- 그러나 크기가 5차 이상인 행렬의 소행렬은 크기가 4차 이상이므로, 이 소행렬에 대한 소행렬을 이용하여 구할 수 있다.
예제 : 다음 정사각 행렬 A에 대한 소행렬과 소행렬식을 구하여라.
$A = \begin{bmatrix} -2 & 2 & -3 \\ 1 & 0 & 1 \\ -4 & 3 & -5 \end{bmatrix}$
$M_{11} = \begin{bmatrix} 0 & 1 \\ 3 & -5 \end{bmatrix}, \quad det(M_{11}) = -3$
$M_{12} = \begin{bmatrix} 1 & 1 \\ -4 & -5 \end{bmatrix}, \quad det(M_{12}) = -1$
$M_{13} = \begin{bmatrix} 1 & 0 \\ -4 & 3 \end{bmatrix}, \quad det(M_{13}) = 3$
$M_{21} = \begin{bmatrix} 2 & -3 \\ 3 & -5 \end{bmatrix}, \quad det(M_{21}) = -1$
$M_{22} = \begin{bmatrix} -2 & -3 \\ -4 & -5 \end{bmatrix}, \quad det(M_{22}) = -2$
$M_{23} = \begin{bmatrix} -2 & 2 \\ -4 & 3 \end{bmatrix}, \quad det(M_{23}) = 2$
$M_{31} = \begin{bmatrix} 2 & -3 \\ 0 & 1 \end{bmatrix}, \quad det(M_{31}) = 2$
$M_{32} = \begin{bmatrix} -2 & -3 \\ 1 & 1 \end{bmatrix}, \quad det(M_{32}) = 1$
$M_{33} = \begin{bmatrix} -2 & 2 \\ 1 & 0 \end{bmatrix}, \quad det(M_{33}) = -2$
여인수(Cofactor :$A_{ij}$)와 여인수 행렬(Cofactor Matrix :$[A_{ij}]$)
`n` 차 정사각 행렬 `A = [a_{ij}]` 에서 원소 `a_{ij}` 에 관한 계수와 그 계수를 원소로 갖는 행렬
$$A_{ij} = (-1)^{i+j} det(M_{ij})$$
- 여인수를 구하는 공식에서 알 수 있듯이, 여인수는 각 행렬의 소행렬식 $det(M_{ij})$ 와 각 원소의 위치에 따른 부호 $(-1)^{i+j}$ 에 의해 결정된다.
- 여인수 행렬에서 각 원소의 위치에 따른 원소의 부호는 다음과 같다.
$$\begin{bmatrix} + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix}$$

예 : 행렬 $A = \begin{bmatrix} 11 & 12 & 13 & 14 \\ 21 & 22 & 23 & 24 \\ 31 & 32 & 33 & 34 \\ 41 & 42 & 43 & 44 \end{bmatrix}$ 에서 `a_{11}` 과 `a_{43}` 의 여인수 구하기
- 여인수 `A_{11}` 의 부호는 $(-1)^{1+1}$ 이 되어 양수(+)이고, `A_{43}` 의 부호는 $(-1)^{4+3}$ 이 되어 음수(-)이다.
| $A_{11} = (-1)^{1 + 1} det(M_{11}) = det(M_{11})$ $= \{(22 × 33 × 44 + 23 × 34 × 42 + 24 × 32 × 43) - (24 × 33 × 42 + 22 × 34 × 43 + 23 × 32 × 44)\}$ $A_{43} = (-1)^{4 + 3} det(M_{43}) = -det(M_{43})$ $= - \{ (11 × 22 × 34 + 12 × 24 × 31 + 14 × 21 × 32) - (14 × 22 × 31 + 12 × 21 × 34 + 11 × 24 × 32) \}$ |
예제 : 다음 정사각 행렬 A에 대한 여인수 행렬을 구하여라.
$A = \begin{bmatrix} -2 & 2 & -3 \\ 1 & 0 & 1 \\ -4 & 3 & -5 \end{bmatrix}$
$A_{11} = (-1)^{1+1} det(M_{11}) = -3$
$A_{12} = (-1)^{1+2} det(M_{12}) = -(-1) =1$
$A_{13} = (-1)^{1+3} det(M_{13}) = 3$
$A_{21} = (-1)^{2+1} det(M_{21}) = -(-1) =1$
$A_{22} = (-1)^{2+2} det(M_{22}) = -2$
$A_{23} = (-1)^{2+3} det(M_{23}) = -2$
$A_{31} = (-1)^{3+1} det(M_{31}) = 2$
$A_{32} = (-1)^{3+2} det(M_{32}) = -1$
$A_{33} = (-1)^{3+3} det(M_{33}) = -2$
$∴ [A_{ij}] = \begin{bmatrix} -3 & 1 & 3 \\ 1 & -2 & -2 \\ 2 & -1 & -2 \end{bmatrix}$
여인수를 이용한 행렬식
`n ≥ 3` 인 `n` 차 정사각 행렬 `A` 의 행렬식은 다음과 같다.
$det(A)$
$= a_{i1}A_{i1} + a_{i2}A_{i2} + \cdots + a_{in}A_{in}$ : `i` 행을 선택한 경우
$= a_{1j}A_{1j} + a_{2j}A_{2j} + \cdots + a_{nj}A_{nj}$ : `j` 열을 선택한 경우
- 여인수를 이용하여 행렬식을 구할 때는 행렬의 한 행 또는 한 열을 선택하고, 그 행이나 열을 구성하는 각 원소와 그 원소에 대응되는 여인수를 곱한 다음 더하여 행렬식을 구한다.
- 이 때, 어떤 행 또는 어떤 열을 선택하더라도 행렬식 결과는 같으므로, 연산하기 쉬운 행이나 열을 선택한다.
예 : $A = \begin{bmatrix} -2 & 2 & -3 \\ 1 & 0 & 1 \\ -4 & 3 & -5 \end{bmatrix}$ 의 행렬식 구하기
- 행렬 `A` 의 여인수 행렬은 다음과 같다.
| $ [A_{ij}] = \begin{bmatrix} -3 & 1 & 3 \\ 1 & -2 & -2 \\ 2 & -1 & -2 \end{bmatrix}$ |
- 행렬식을 구하기 위해 연산하기 쉬운 2행을 선택한다. 그러면 다음과 같이 행렬 `A` 의 2행의 원소들과 행렬 `A` 에 대한 여인수 행렬의 2행의 원소들을 곱한 후 더해서 행렬식을 구할 수 있다.
| $det(A) = a_{21}A_{21} + a_{22}A_{22} + a_{23}A_{23}$ $= a_{21}(-1)^{2+1}det(M_{21}) + a_{22}(-1)^{2+2}det(M_{22}) + a_{23}(-1)^{2+3}det(M_{23})$ $= (1 × 1) + \{ 0 × (-2) \} + \{ 1 × (-2) \} = -1$ |
- 열을 선택해도 같은 행렬식이 나오는데, 이를 확인하기 위해 역시 연산이 간단한 2열을 선택하여 행렬식을 구해본다.
| $det(A) = a_{12}A_{12} + a_{22}A_{22} + a_{32}A_{32}$ $= a_{12}(-1)^{1+2}det(M_{12}) + a_{22}(-1)^{2+2}det(M_{22}) + a_{32}(-1)^{3+2}det(M_{32})$ $= (2 × 1) + \{ 0 × (-2) \} + \{ 3 × (-1) \} = -1$ |
- 그러므로 여인수를 이용하여 행렬식을 구할 때는 어떤 행 또는 어떤 열을 선택해도 상관 없다.
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 집합의 종류 (0) | 2022.10.22 |
|---|---|
| [이산 수학] 집합의 개념 (0) | 2022.10.22 |
| [이산 수학] 행렬과 연립 일차 방정식 (1) | 2022.10.13 |
| [이산 수학] 역행렬 (0) | 2022.10.12 |
| [이산 수학] 행렬의 종류 (0) | 2022.10.12 |
| [이산 수학] 행렬의 연산 (1) | 2022.10.11 |
| [이산 수학] 행렬의 개념 (1) | 2022.10.11 |
| [이산 수학] 수학적 귀납법 (0) | 2022.10.10 |
