모평균의 검정 (σ² : 미지)
- 이전 글에서는 모집단의 분산을 알고 있는 경우에 모평균과 두 모평균 차에 대한 주장을 검정하는 방법을 살펴보았다.
- 그러나 대부분의 모집단은 모분산이 알려져 있지 않다.
- 따라서 모분산을 모르는 경우에 모평균에 대한 주장을 검정하는 방법을 살펴볼 필요가 있다.
- 모분산이 알려져 있지 않은 경우에는 정규 분포와 매우 흡사한 `t`-분포를 사용한다.
- 이 페이지에서는 `t`-분포를 이용하여 모분산이 알려져 있지 않은 정규 모집단의 모평균과 두 모평균의 차에 대한 주장을 검정하는 방법을 살펴본다.
`t`-검정(`t`-Test)

- 근대 통계학의 기초가 되는 소표본론에서 많은 업적을 남긴 영국의 통계학자인 윌리엄 고셋(William Sealey Gosset, 1876-1937)이 소표본을 분석하기 위해 고안한 검정 방법이다.
- 이 분포는 1908년에 Student's t-분포라는 필명으로 발표한 논문에서 처음으로 사용하면서 알려졌으며, 이러한 이유로 `t`-분포를 Student's `t`-분포라고도 한다.
- 이 분포는 표준 정규 분포와 매우 흡사하며, 모분산이 알려지지 않은 정규 모집단에서 소표본을 추출하여 모평균을 추론할 때 주로 사용한다.
`t`- 분포(`t`-Distribution)
- 표본의 크기가 작은 경우, 즉 `n < 30` 인 경우에 모평균 또는 모평균 차의 추론에 사용하며, 다음과 같이 정의한다.
연속 확률 변수 `X` 의 확률 밀도 함수 `f(x)` 가 다음과 같을 때, 확률 변수 `X` 는 자유도 `n` 인 `t`-분포(T-Distribution)을 따른다고 하고, $X \sim t(n)$ 으로 나타낸다.
$$f(x) = \frac{Γ \left( \frac{n + 1}{2} \right)}{\sqrt{nπ} \; Γ \left( \frac{n}{2} \right)} \left ( 1 + \frac{x^{2}}{n} \right )^{-\frac{n + 1}{2}}, \quad -\infty < x < \infty$$
특성
- `t`-분포는 표준 정규 분포와 비교하여 다음과 같은 특성을 갖는다.
① 분포 곡선은 `x = 0` 에서 최댓값을 갖고, 좌우 대칭이다.
② 분포 곡선은 표준 정규 분포와 같이 종 모양이다.
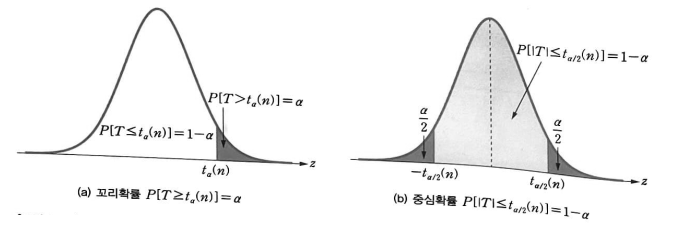
③ `t`-분포의 꼬리 부분이 표준 정규 분포보다 약간 두텁다. (a)
④ 자유도 `n` 이 증가하면 `t`-분포는 표준 정규 분포에 근접하게 된다. (b)

- 일반적으로 자유도 `n` 인 `t`-분포에서 $100(1 - \alpha)$% 백분위수 $t = t_{\alpha}(n)$ 으로 나타낸다.
- 즉, 오른쪽 꼬리 확률 $α$ 에 대해 $P[T > t_{\alpha}(n)] = \alpha$ 이다.
- 그러면 `t`-분포는 `x = 0` 에 대해 대칭이므로 다음이 성립한다.
$$P[T \ge t_{\alpha}(n)] = P[T \le -t_{\alpha}(n)] = \alpha$$
$$P[|T| \le t_{\frac{\alpha}{2}}(n)] = 1 - \alpha$$
- 아래 그림은 이와 같은 성질을 보여준다.
`t`-분포표를 이용하여 백분위수 계산
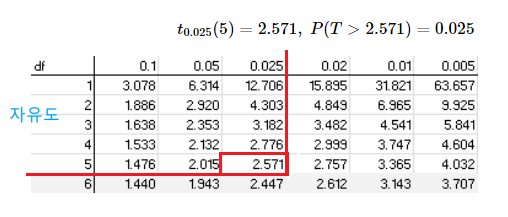
- 자유도 `n` 인 `t`-분포에서 오른쪽 꼬리 확률이 `α` 인 $100(1 - α)$% 백분위수 $t_{\alpha}(n)$ 을 구하기 위해서는 $\color{#6164C6}t$-분포표($\color{#6164C6}t$-Distribution Table)를 이용한다.
- 예를 들어, 자유도가 5인 `t`-분포에서 97.5% 백분위수 $t_{0.025}(5)$ 를 다음과 같이 `t`-분포표를 이용하여 구할 수 있다.
| ① 자유도를 나타내는 d.f 열에서 5를 선택한다. ② 오른쪽 꼬리 확률을 나타내는 $\alpha$ 행에서 0.025를 선택한다. ③ d.f가 5인 행과 `α` 가 0.025인 열이 만나는 수 2.571을 선택한다. ④ $t_{0.025}(5) = 2.571$ 이다. 즉, $P(X \le 2.571) = 0.975$ 또는 $P(X \ge 2.571) = 0.025$ |
`t`-분포표(`t`-Distribution Table)
`t`-검정(`t`-Test)
- 모분산 $\sigma^{2}$ 을 모르는 정규 모집단의 모평균 $\mu$ 에 대한 주장을 검정하는 방법을 살펴보자.
- 만약 모분산 $\sigma^{2}$ 을 알고 있다면, 크기 `n` 인 표본 평균의 표준화 화률 변수 `Z` 는 다음과 같다.
| $$Z = \frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim t(n - 1)$$ |
- 그러나 모분산 $\sigma^{2}$ 을 모르기 때문에 검정 통계량 `Z` 와 표준 정규 분포를 사용할 수 없다. 한편, 크기 `n` 인 표본의 표본 분산 $s^{2}$ 또는 표본 표준 편차 `s` 를 구할 수 있다.
- 이 때, 검정 통계량 `Z` 에서 알려지지 않은 모표준 편차 $\sigma$ 대신에 표본 표준 편차 `s` 로 대치한 표본 평균의 표준화 확률 변수 `T` 는 다음과 같이 자유도가 `n - 1` 인 `t`-분포를 따르는 것이 알려져 있다.
$$T = \frac{\overline{X} - \mu}{\frac{s}{\sqrt{n}}} \sim t(n - 1)$$
- 따라서 모분산을 모르는 정규 모집단의 모평균에 대한 귀무 가설 $H_{0} : \mu = \mu_{0}$ 를 검정하기 위한 검정 통계량은 다음과 같다.
$$T = \frac{\overline{X} - \mu_{0}}{\frac{s}{\sqrt{n}}} \sim t(n - 1)$$
- 그러므로 모분산을 모르는 모집단 분포의 모평균에 대한 주장의 진위 여부를 검정하기 위해 자유도 `n - 1` 인 `t`-분포를 사용하며, 다음과 같은 순서로 구한다.
① 귀무 가설 $H_{0}$ 와 대립 가설 $H_{1}$ 을 설정한다.
② 유의 수준 $\alpha$ 를 정한다.
③ 검정 통계량 $\displaystyle \frac{\overline{X} - \mu_{0}}{\frac{s}{\sqrt{n}}}$ 를 선택한다.
④ 유의 수준 $\alpha$ 에 대한 임계값과 기각역을 구한다.
⑤ 표본으로부터 검정 통계량의 관찰값 $t_{0}$ 를 구하고, $H_{0}$ 의 채택과 기각 여부를 결정한다.
- 이 때, 미리 주어진 유의 수준 $\alpha$ 에 대한 기각역과 채택역에 대해 검정 통계량의 관찰값이 기각역 안에 있으면 귀무 가설 $H_{0}$ 를 기각하고, 그렇지 않으면 $H_{0}$ 를 기각하지 못한다.
단일 모평균에 대한 검정
- 모분산 $\sigma^{2}$ 를 모르는 정규 모집단에서 모평균에 대한 귀무 가설 $H_{0}$ 와 대립 가설 $H_{1}$ 에 대해 다음과 같이 검정한다.
양측 검정
- 귀무 가설 $H_{0} : \mu = \mu_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : \mu \ne \mu_{0}$ 를 검정하는 방법을 살펴보자.
- 이 때, 사용하는 검정 통계량과 확률 분포는 다음과 같다.
| $$T = \frac{\overline{X} - \mu_{0}}{\frac{s}{\sqrt{n}}} \sim t(n - 1)$$ |
- 먼저 표본 평균의 관찰값 $\overline{x}$ 와 표본 표준 편차 `s` 에 대해 검정 통계량의 관찰값 $t_{0}$ 를 구한다.
| $$t_{0} = \frac{\overline{x} - \mu_{0}}{\frac{s}{\sqrt{n}}}$$ |
- 그리고 유의 수준 $\alpha$ 에 대한 임계값 $t_{\frac{\alpha}{2}}(n - 1)$ 을 `t`-분포표에서 찾으면 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같다.
$$T \le -t_{\frac{\alpha}{2}}(n - 1), \quad T \ge t_{\frac{\alpha}{2}}(n - 1)$$
- 이 때, 검정 통계량의 관찰값 $t_{0}$ 가 기각역 안에 놓이면 귀무 가설 $H_{0}$ 를 기각한다.
예제 : 정규 모집단의 평균이 26.5 라는 주장을 알아보기 위해 표본 조사를 실시하여 다음을 얻었다. 이 주장에 대해 유의 수준 5%에서 검정하라.
| 표본 | 표본의 크기 | 표본 평균 | 표본 표준 편차 |
| A | 16 | 29 | 4.8 |
(1)
귀무 가설 $H_{0} : \mu = 26.5$ 와 대립 가설 $H_{1} : \mu \ne 26.5$ 를 설정한다.
(2)
$α = 0.05$ 에 대해 $t_{0.025}(15) = 2.131$ 이므로 기각역은 다음과 같다.
| $$T \le -2.131, \quad T \ge 2.131$$ |
(3)
`n = 16, s = 4.8` 이므로 검정 통계량을 구하면 다음과 같다.
| $$T = \frac{\overline{X} - 26.5}{4.8 / \sqrt{16}} = \frac{\overline{X} - 26.5}{1.2}$$ |
(4)
$\overline{x} = 29$ 이므로 검정 통계량의 관찰값은 $\displaystyle t_{0} = \frac{29 - 26.5}{1.2} = 2.08$ 이다.
(5)
$t_{0} = 2.08$ 이 기각역 안에 놓이지 않으므로 귀무 가설을 기각할 수 없다. 즉, 모평균이 26.5라는 주장은 근거가 충분하다.
상단측 검정
- 귀무 가설 $H_{0} : \mu \le \mu_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : \mu > \mu_{0}$ 를 검정하는 방법을 살펴보자.
- 미리 설정된 유의 수준 $\alpha$ 에 대한 검정 통계량 `T` 에 대해 오른쪽 꼬리 확률이 $α$ 인 임계점은 $t_{\alpha}(n - 1)$ 이다.
- 그리고 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같으며, 검정 통계량의 관찰값 $t_{0}$ 가 기각역 안에 놓이면 귀무 가설 $H_{0}$ 를 기각한다.
$$T \ge t_{\alpha}(n - 1)$$
예제 : 정규 모집단의 귀무 가설 $H_{0} : \mu \le 45$ 를 확인하기 위해 표본 조사를 실시하여 다음을 얻었다.
| 표본 | 표본의 크기 | 표본 평균 | 표본 표준 편차 |
| A | 25 | 46.2 | 2.75 |
(a) 이 주장에 대해 유의 수준 5%에서 검정하라.
(b) 이 주장에 대해 유의 수준 1%에서 검정하라.
[a]
유의 수준 $\alpha = 0.05$ 에서 다음 순서에 따라 $H_{0} : \mu \le 45$ 를 검정한다.
(a-1)
귀무 가설 $H_{0} : \mu = 45$ 와 대립 가설 $H_{1} : \mu > 45$ 를 설정한다.
(a-2)
$α = 0.05$ 에 대해 $t_{0.05}(24) = 1.711$ 이므로 기각역은 $T \ge 1.711$ 이다.
(a-3)
`n = 25, s = 2.75` 이므로 검정 통계량을 구하면 다음과 같다.
| $$T = \frac{\overline{X} - 45}{2.75 / \sqrt{25}} = \frac{\overline{X} - 45}{0.55}$$ |
(a-4)
$\overline{x} = 46.2$ 이므로 검정 통계량의 관찰값은 $\displaystyle t_{0} = \frac{46.2 - 45}{0.55} = 2.182$ 이다.
(a-5)
$t_{0} = 2.182$ 는 기각역 안에 놓이므로 귀무 가설을 기각한다.
[b]
유의 수준이 $α = 0.01$ 이므로 $t_{0.01}(24) = 2.492$ 이다.
따라서 기각역은 $T \ge 2.492$ 이고 관찰값 $t_{0} = 2.182$ 는 기각역 안에 놓이지 않는다.
그러므로 귀무 가설을 기각할 수 없다.
하단측 검정
- 귀무 가설 $H_{0} : \mu \ge \mu_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : \mu < \mu_{0}$ 를 검정하는 방법을 살펴보자.
- 미리 설정된 유의 수준 $\alpha$ 에 대한 검정 통계량 `T` 에 대해 왼쪽 꼬리 확률이 $α$ 인 임계점은 $-t_{\alpha}(n - 1)$ 이다.
- 그리고 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같으며, 검정 통계량의 관찰값 $t_{0}$ 가 기각역 안에 놓이면 귀무 가설 $H_{0}$ 를 기각한다.
$$T \le -t_{\alpha}(n - 1)$$
예제 : 성인이 컴퓨터 화면에 있는 텍스트 한 쪽을 읽는 데 걸리는 시간은 평균 48초 이상이라고 한다. 이를 확인하기 위해 표본 조사를 실시하여 다음을 얻었다. 이 주장에 대해 유의 수준 5%에서 검정하라.
| 표본 | 표본의 크기 | 표본 평균 | 표본 표준 편차 |
| A | 15 | 46.2 | 3.84 |
(1)
귀무 가설 $H_{0} : \mu \ge 48$ 과 대립 가설 $H_{1} : \mu < 48$ 를 설정한다.
(2)
$α = 0.05$ 에 대해 $t_{0.05}(14) = 1.761$ 이므로 기각역은 $T \le -1.761$ 이다.
(3)
`n = 15, s = 3.84` 이므로 검정 통계량을 구하면 다음과 같다.
| $$T = \frac{\overline{X} - 48}{3.84 / \sqrt{15}} = \frac{\overline{X} - 48}{0.9915}$$ |
(4)
$\overline{x} = 46.2$ 이므로 검정 통계량의 관찰값은 $\displaystyle t_{0} = \frac{46.2 - 48}{0.9915} = -1.8154$ 이다.
(5)
$t_{0} = -1.8154$ 는 기각역 안에 놓이므로 귀무 가설을 기각한다.
`p`-값을 이용한 검정 방법
- 귀무 가설에 대한 타당성을 검정하기 위해 `p`-값을 이용한 방법은 다음과 같다.
① 귀무 가설 $H_{0}$ 와 대립 가설 $H_{1}$ 을 설정한다.
② 유의 수준 `α` 를 정한다.
③ 표본으로부터 표본 평균 $\overline{x}$ 와 표본 표준 편차 $s$ 를 구한다.
④ 검정 통계량 $\displaystyle \frac{\overline{X} - \mu_{0}}{\frac{s}{\sqrt{n}}}$ 를 선택하고, 관찰값 $t_{0}$ 를 구한다.
⑤ `p`-값을 구한다.
⑥ $p-값 \le \alpha$ 이면 귀무 가설을 기각하고, $p-값 > \alpha$ 이면 귀무 가설을 채택한다.
- 그리고 모분산을 모르고 소표본(`n < 30`)인 경우에 귀무 가설 $H_{0}$ 에 대한 검정은 다음과 같이 정리할 수 있다.
| 검정 방법 \ 가설과 기각역 | 귀무 가설 $H_{0}$ | 대립 가설 $H_{1}$ | $H_{0}$ 의 기각역 | `p`-값 |
| 하단측 검정 | $\mu \le \mu_{0}$ | $\mu <\mu_{0}$ | $R : T \le -t_{\alpha}(n - 1)$ | $P(T < t_{0})$ |
| 상단측 검정 | $\mu \le \mu_{0}$ | $\mu > \mu_{0}$ | $R : T \ge t_{\alpha}(n - 1)$ | $P(T > t_{0})$ |
| 양측 검정 | $\mu = \mu_{0}$ | $\mu \ne \mu_{0}$ | $R : |T| \ge t_{\frac{\alpha}{2}}(n - 1)$ | $P(|T| > t_{0})$ |
예제 : 성인이 컴퓨터 화면에 있는 텍스트 한 쪽을 읽는 데 걸리는 시간은 평균 48초 이상이라고 한다. 이를 확인하기 위해 표본 조사를 실시하여 다음을 얻었다. 이에 대해 `p`-값을 구하고, 유의 수준 5%에서 검정하라.
| 표본 | 표본의 크기 | 표본 평균 | 표본 표준 편차 |
| A | 15 | 46.2 | 3.84 |
`n = 15` 인 하단측 검정이고, 검정 통계량의 관찰값 $t_{0} = -1.8154$ 를 얻었다.
자유도 14인 `t`-분포표에서 $t_{0.05}(14) = 1.761, \; t_{0.025} = 2.145$ 이므로 $-2.145 < t_{0} < -1.761$ 이고 다음을 얻는다.
| $$P(T \le -1.761) = 0.05, \; P(T \le -2.145) = 0.025$$ |
따라서 $0.025 < p-값 < 0.05$ 이고, `p`-값이 유의 수준 5% 보다 작으므로 귀무 가설을 기각한다.
두 모평균 차에 대한 검정
- 독립이고 정규 분포를 따르는 두 모집단의 모분산 $\sigma_{1}^{2}$ 과 $\sigma_{2}^{2}$ 이 알려지지 않은 경우에 두 모평균의 차 $\mu_{1} - \mu_{2}$ 에 대한 가설을 검정하는 방법을 살펴보자.
- 이를 위해 각각 크기 `n` 과 `m` 인 표본을 선정하면 모분산을 모르는 단일 모집단과 동일하게 `t`-분포를 사용하지만 다음과 같은 차이가 있다.
① $\sigma_{1}^{2} = \sigma_{2}^{2} = \sigma^{2}$ 이고 $\sigma^{2}$ 은 미지이다.
② 자유도 $n + m - 2$ 인 `t`-분포를 사용한다.
③ 표본 표준 편차 `s` 대신에 합동 표본 표준 편차 $s_{p}$ 를 사용한다.
- 여기서 합동 표본 분산(Pooled Sample Variance)은 다음과 같이 정의한다.
$$S^{2}_{p} = \frac{1}{n + m - 2} \left [ \sum_{i=1}^{n} (X_{i} - \overline{X})^{2} + \sum_{j = 1}^{m}(Y_{j} - \overline{Y})^{2} \right ] $$
- 그리고 합동 표본 분산의 양의 제곱근을 합동 표본 표준 편차(Pooled Sample Standard Deviation)라 한다.
- 특히 두 표본 분산을 각각 $S_{1}^{2}, \; S_{2}^{2}$ 이라 하면 합동 표본 분산은 다음과 같이 간단히 구할 수 있다.
$$S_{p}^{2} = \frac{1}{n + m - 2}[(n - 1)S_{1}^{2} + (m - 1)S_{2}^{2}]$$
- 이 때, 귀무 가설 $H_{0} : \mu_{1} - \mu_{2} = d_{0}, \; H_{0} : \mu_{1} - \mu_{2} \ge d_{0}, \; H_{0} : \mu_{1} - \mu_{2} \le d_{0}$ 를 검정하기 위해 사용하는 검정 통계량은 다음과 같다.
$$T = \frac{(\overline{X} - \overline{Y}) - d_{0}}{s_{p} \sqrt{\frac{1}{n} + \frac{1}{m}}}$$
- 두 표본으로부터 얻은 표본 평균 $\overline{x}$ 와 $\overline{Y}$ 그리고 표본 분산 $s_{1}^{2}$ 과 $s_{2}^{2}$ 에 의해 검정 통계량의 관찰값 $t_{0}$ 를 구한다.
- 이 때, 관찰값 $t_{0}$ 가 기각역 안에 놓이면 귀무 가설 $H_{0}$ 를 기각하고, 그렇지 않으면 $H_{0}$ 를 기각하지 않는다.
- 한편 `p`-값을 구하여 $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.
- 따라서 두 모분산을 모르는 경우에 모평균의 차 $\mu_{1} - \mu_{2}$ 에 대한 가설 검정의 유형에 대한 기각역과 `p`-값을 정리하면 다음과 같다.
| 검정 방법 \ 가설과 기각역 | 귀무 가설 $H_{0}$ | 대립 가설 $H_{1}$ | $H_{0}$ 의 기각역 | `p`-값 |
| 하단측 검정 | $\mu_{1} - \mu_{2} \ge d_{0}$ | $\mu_{1} - \mu_{2} < d_{0}$ | $T \le -t_{\alpha}(n + m - 2)$ | $P(T < t_{0})$ |
| 상단측 검정 | $\mu_{1} - \mu_{2} \le d_{0}$ | $\mu_{1} - \mu_{2} > d_{0}$ | $T \ge t_{\alpha}(n + m - 2)$ | $P(T > t_{0})$ |
| 양측 검정 | $\mu_{1} - \mu_{2} = d_{0}$ | $\mu_{1} - \mu_{2} \ne d_{0}$ | $|T| \ge t_{\frac{α}{2}}(n + m - 2)$ | $2[1 - P(T < t_{0})]$ |
예제 : 독립인 두 정규 모집단의 모평균에 대해 $\mu_{1} - \mu_{2} = 2$ 라는 주장을 검정하기 위해 표본을 선정하여 다음 결과를 얻었다. 이 주장에 대해 유의 수준 5%에서 검정하라.
| 표본 | 표본의 크기 | 표본 평균 | 표본 표준 편차 |
| 표본 1 | 10 | $\overline{x} = 18.7$ | $s_{1} = 2.4$ |
| 표본 2 | 8 | $\overline{y} = 14.2$ | $s_{2} = 3.1$ |
(1)
귀무 가설 $H_{0} : \mu_{1} - \mu_{2} = 2$ 와 대립 가설 $H_{1} : \mu_{1} - \mu_{2} \ne 2$ 를 설정한다.
(2)
$\alpha = 0.05$ 에 대해 $t_{0.025}(16) = 2.12$ 이므로 기각역은 $T \le -2.12, \; T \ge 2.12$ 이다.
(3)
$n = 10, \; s_{1} = 2.4, \; m = 8, \; s_{2} = 3.1$ 이므로 합동 표본 분산을 구하면 다음과 같다.
| $$s_{p}^{2} = \frac{1}{10 + 8 - 2}(9 \times 2.4^{2} + 7 \times 3.1^{2}) = 7.4444$$ |
따라서 합동 표본 표준 편차는 $s_{p} = \sqrt{7.4444} = 2.728$ 이다.
(4)
검정 통계량을 구하면 다음과 같다.
| $$T = \frac{(\overline{X} - \overline{Y}) - 2}{2.728 \times \sqrt{\frac{1}{10} + \frac{1}{8}}} = \frac{(\overline{X} - \overline{Y}) - 2}{1.294}$$ |
(5)
$\overline{x} = 18.7, \; \overline{y} = 14.2$ 이므로 검정 통계량의 관찰값은 $\displaystyle t_{0} = \frac{(18.7 - 14.2) - 2}{1.294} = 1.932$ 이다.
(6)
$t_{0} = 1.932$ 는 기각역 안에 놓이지 않으므로 귀무 가설을 기각할 수 없다.
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모비율의 검정 (0) | 2022.12.01 |
|---|---|
| [확률과 통계] 모평균의 검정(σ² : 기지) (0) | 2022.11.30 |
| [확률과 통계] 통계적 가설 검정 (0) | 2022.11.28 |
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
