728x90
728x90
통계적 가설 검정
- 어느 학원에서 합격률이 전국 최고인 85.4% 라는 광고를 한다고 하자. 그러면 이 학원의 주장이 참인지 아니면 거짓인지 확인할 필요가 있을 것이다.
- 이와 같이 모수에 대한 주장을 검정하기 위해 반대인 주장을 설정하고, 어느 주장이 참인지 검정하는 일반적인 방법을 살펴본다.
가설 검정의 의미
- 합격률이 전국 최고인 85.4% 라는 광고가 참인지 확인하기 위해서는, 이 주장을 타당한 것으로 인정하고 이와 반대되는 주장을 설정한다.
- 그리고 이러한 두 주장 중에서 어느 것이 참인지 결정해야 한다.
- 이 때, 임의로 표본을 선정하고, 검정을 위한 표본 통계량을 이용하여 얻은 정보를 근거로 어느 주장이 참인지 판정한다.
- 이와 같이 참인지 거짓인지 명확히 밝히고자 하는 모수에 대한 주장을 가설(Hypothesis)이라 한다.
- 그리고 표본으로부터 얻은 통계량을 이용하여 모수에 대한 주장의 진위 여부를 검정하는 과정을 가설 검정(Hypothesis Testing)이라 한다.
- 이 때, "합격률이 85.4%이다." 라는 주장과 이에 반대되는 주장인 "합격률이 85.4%가 아니다." 를 설정한다.
- 학원 측의 주장과 같이 통계적으로 검증받아야 할 주장을 귀무 가설이라 하고, 귀무 가설을 부정하는 가설을 대립 가설이라 한다.
귀무 가설(Null Hypothesis)와 대립 가설(Alternative Hypothesis)
- 귀무 가설(Null Hypothesis) : 거짓이 명확히 구명될 때까지 참인 것으로 인정되는 모수에 대한 주장
- 대립 가설(Alternative Hypothesis) : 귀무 가설이 거짓이라면 참이 되는 가설
- 귀무 가설은 타당성을 입증해야 할 가설을 의미하고 $H_{0}$ 로 나타낸다.
- 대립 가설은 귀무 가설을 부정하는 새로운 가설을 의미하고 $H_{1}$ 으로 나타낸다.
- 귀무 가설에는 항상 등호(`=`) 를 사용하고, 대립 가설에는 등호를 사용하지 않는다.
- 예를 들어, 합격률 `p` 에 대한 귀무 가설은 다음과 같다.
| $$H_{0} : p \le 0.854. \quad H_{0} : p = 0.854, \quad H_{0} : p \ge 0.854$$ |
- 그리고 이에 반대되는 대립 가설은 각각 다음과 같다.
| $$H_{1} : p > 0.854. \quad H_{1} : p ≠ 0.854, \quad H_{1} : p < 0.854$$ |
- 한편, 임의로 선정한 표본을 이용하여 귀무 가설 $H_{0}$ 의 진위 여부를 검정하며, 검정을 위해 사용하는 표본 통계량을 검정 통계량이라고 한다.
검정 통계량(Test Statistic)
귀무 가설 $H_{0}$ 의 진위 여부를 판정하기 위해 표본으로부터 얻은 통계량
- 검정 통계량의 관찰값을 이용하여 귀무 가설이 거짓으로 판정된다면 귀무 가설 $H_{0}$ 를 기각(Reject)한다고 한다.
- 그리고 귀무 가설을 부정하지 못하는 경우에는 귀무 가설 $H_{0}$ 를 채택(Accept)한다고 한다.
- 이 때, 귀무 가설을 기각하는 검정 통계량의 영역을 기각역이라 하고, 반대로 귀무 가설을 채택하는 영역을 채택역이라고 한다.
채택역(Acceptance Region)과 기각역(Critical Region)
- 채택역(Acceptance Region) : 귀무 가설 $H_{0}$ 를 채택하는 검정 통계량의 영역(범위)
- 기각역(Critical Region) : 귀무 가설 $H_{0}$ 를 기각하는 검정 통계량의 영역(범위)
- 한편, 표본을 아무리 공정하게 선정하더라도 귀무 가설 $H_{0}$ 가 실제로 참이지만 검정 결과는 참 또는 거짓으로 판정하는 경우가 발생한다.
- 그리고 반대로 $H_{0}$ 가 실제로 거짓이지만 검정 결과는 참 또는 거짓으로 판정하는 경우가 발생한다.
- 이 때, 실제로 $H_{0}$ 가 참(또는 거짓)이고 검정 결과도 $H_{0}$ 를 채택(또는 기각)한다면 올바른 결정을 하게 된다.
- 그러나 $H_{0}$ 가 실제로 참이지만, 검정한 결과 $H_{0}$ 를 기각한다거나, 반대로 $H_{0}$ 가 실제로 거짓이지만 검정한 결과 $H_{0}$ 를 채택한다면 오류를 범하게 된다.
- 이 때, 다음과 같이 참인 귀무 가설을 기각함으로써 발생하는 오류를 제1종 오류, 거짓인 귀무 가설을 채택함으로써 발생하는 오류를 제2종 오류라 한다.
| 검정 결과 \ 실제 | $H_{0}$ 가 참 | $H_{0}$ 가 거짓 |
| $H_{0}$ 를 채택 | 올바른 결정 | 제2종 오류 |
| $H_{0}$ 를 기각 | 제1종 오류 | 올바른 결정 |
- 그리고 제1종 오류를 범할 확률의 최대 허용 한계를 유의 수준이라 하며, 전통적으로 유의 수준 `α` 는 0.01(1%), 0.05(5%), 0.1(10%)을 많이 사용한다.
- 유의 수준 $α = 0.05$ 라 함은 원칙적으로 기각할 것을 예상하여 설정한 가설을 기각한다고 하더라도, 그것에 의한 오차가 최대 5%임을 나타낸다.
제1종 오류(Type I Error)와 유의 수준(Significance Level)
- 제1종 오류(Type I Error) : 귀무 가설 $H_{0}$ 가 참이지만 검정 결과 귀무 가설을 기각함으로써 발생하는 오류
- 유의 수준(Significance Level) : 제1종 오류를 범할 확률 `α`
기각역을 이용한 검정 방법
- 귀무 가설 $H_{0}$ 에 대한 주장, 즉 모평균 `μ` 또는 모비율 `p` 와 같은 모수 `θ` 에 대한 주장은 부등호($\le, \ge$) 또는 등호(`=`) 를 사용한다.
- 따라서 이러한 귀무 가설에 대립되는 대립 가설 $H_{1}$ 을 설정하며, 각 경우의 검정 유형은 다음과 같다.
| 검정 유형 | 귀무 가설 | 대립 가설 |
| 양측 검정 | $H_{0} : θ = θ_{0}$ | $H_{1} : θ \ne θ_{0}$ |
| 상단측 검정 | $H_{0} : θ \le θ_{0}$ | $H_{1} : θ > θ_{0}$ |
| 하단측 검정 | $H_{0} : θ \ge θ_{0}$ | $H_{1} : θ < θ_{0}$ |
- 그러면 귀무 가설은 다음 순서에 따라 검정한다.
① 귀무 가설 $H_{0}$ 와 대립 가설 $H_{1}$ 을 설정한다.
② 유의 수준 `α` 를 정한다.
③ 적당한 검정 통계량을 선택한다.
④ 유의 수준 `α` 에 대한 임계값과 기각역을 구한다.
⑤ 검정 통계량의 관찰값을 구하여, 이 값이 기각역 안에 놓이면 $H_{0}$ 를 기각한다.
- 이 때, 미리 주어진 유의 수준 `α` 에 대한 검정 유형별 $H_{0}$ 의 기각역과 채택역은 다음과 같다.

- 검정 통계량의 관찰값이 기각역 안에 놓이면 $H_{0}$ 를 기각하고, 관찰값이 채택역 안에 놓이면, $H_{0}$ 를 기각하지 못한다.
양측 검정(Two Sided Hypothesis)
- 두 가설 $H_{0} : θ = θ_{0}, \; H_{1} : θ \ne θ_{0}$ 에 대해 유의 수준을 `α` 라 하자.
- 그러면 양쪽 꼬리 확률이 각각 `α / 2` 가 되는 두 임계값 $±z_{\frac{α}{2}}$ 에 대해 기각역은 다음과 같다.
$$Z \le - z_{\frac{α}{2}}, \quad Z \ge z_{\frac{α}{2}}$$
- 즉, 양측 검정의 기각역과 채택역은 다음 그림과 같다.
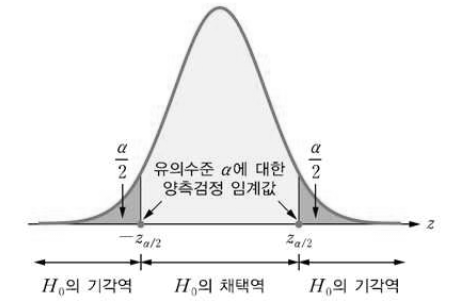
- 따라서 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \le -z_{\frac{α}{2}}$ 또는 $z_{0} \ge z_{\frac{α}{2}}$ 이면 $H_{0}$ 를 기각하고 $-z_{\frac{α}{2}} < z_{0} < z_{\frac{α}{2}}$ 이면 $H_{0}$ 를 기각하지 못한다.
- 이 때, 채택역은 신뢰도 $100(1 - α)$% 신뢰 구간과 일치한다.
상단측 검정(One Sided Upper Hypothesis)
- 두 가설 $H_{0} : θ \le θ_{0}, \; H_{1} : θ > θ_{0}$ 에 대해 유의 수준을 `α` 라 하자.
- 그러면 위쪽 꼬리 확률이 `α` 가 되는 임계값 $z_{α}$ 에 대해 기각역은 다음과 같다.
$$Z \ge z_{α}$$
- 즉, 상단측 검정의 기각역과 채택역은 다음 그림과 같다.
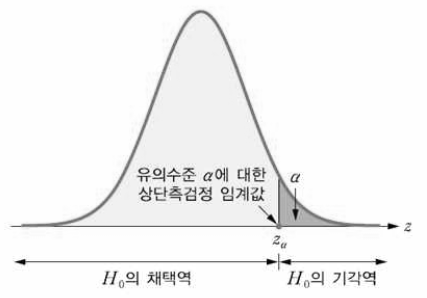
- 따라서 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \ge z_{α}$ 이면 $H_{0}$ 를 기각하고, $z_{0} < z_{α}$ 이면 $H_{0}$ 을 기각하지 못한다.
하단측 검정(One Sided Lower Hypothesis)
- 두 가설 $H_{0} : θ \ge θ_{0}, \; H_{1} : θ < θ_{0}$ 에 대해 유의 수준을 `α` 라 하자.
- 그러면 아래쪽 꼬리 확률이 `α` 가 되는 임계값 $-z_{α}$ 에 대해 기각역은 다음과 같다.
$$Z \le -z_{α}$$
- 즉, 하단측 검정의 기각역과 채택역은 다음 그림과 같다.

- 따라서 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \le -z_{α}$ 이면 $H_{0}$ 를 기각하고, $z_{0} > -z_{α}$ 이면 $H_{0}$ 을 기각하지 못한다.
`p`-값을 이용한 검정 방법
- 기각역을 이용하여 $H_{0}$ 의 기각 또는 채택을 결정하는 방법 이외에 `p`-값을 이용하는 방법이 있다.
- 예를 들어, 귀무 가설 $H_{0}$ 에 대한 상단측 검정에서 검정 통계량의 관찰값이 $z_{0} = 1.9$ 라 하자.
- 그러면 다음과 같이 유의 수준이 $α = 5$% 이면 기각역은 $z \ge 1.645$ 이고 관찰값 $z_{0}$ 이 기각역 안에 들어가므로 유의 수준 5% 에서 귀무 가설을 기각한다.

- 그러나 유의 수준을 $α = 1$% 라 하면 기각역이 $z \ge 2.33$ 이므로 관찰값 $z_{0}$ 가 채택역 안에 들어가고, 유의 수준 1%에서 귀무 가설을 기각할 수 없다.
- 이 때, 관찰값 $z_{0} = 1.9$ 에 의해 귀무 가설 $H_{0}$ 를 기각시킬 가장 작은 확률은 $P(Z \ge 1.9) = 0.0287$ 이고, 이 확률은 $H_{0}$ 를 기각시킬 가장 작은 유의 수준이다.
- 이와 같이 $H_{0}$ 를 기각시킬 가장 작은 유의 수준을 `p`-값이라 한다.
- 그러면 관찰값 $z_{0} = 1.9$ 에 대해 $0.01 < p-값 < 0.05$ 임을 알 수 있다.
`p`-값
귀무 가설 $H_{0}$ 를 참이라고 가정할 때, 관찰값에 의해 $H_{0}$ 를 기각시키는 가장 작은 유의 수준
- 따라서 `p`-값이 주어진 유의 수준보다 작으면 귀무 가설 $H_{0}$ 를 기각하고, `p`-값이 유의 수준보다 크면 $H_{0}$ 를 기각할 수 없다.
- 그러면 `p`-값과 유의 수준 `α` 에 따른 귀무 가설 $H_{0}$ 의 기각 및 채택을 정리하면 다음과 같다.
| `p`-값 | 유의 수준(`α`) | ||
| 10% | 5% | 1% | |
| $p \ge 0.01$ | $H_{0}$ 를 채택 | $H_{0}$ 를 채택 | $H_{0}$ 를 채택 |
| $0.05 \le p < 0.1$ | $H_{0}$ 를 기각 | $H_{0}$ 를 채택 | $H_{0}$ 를 채택 |
| $0.01 \le p < 0.05$ | $H_{0}$ 를 기각 | $H_{0}$ 를 기각 | $H_{0}$ 를 채택 |
| $p < 0.01$ | $H_{0}$ 를 기각 | $H_{0}$ 를 기각 | $H_{0}$ 를 기각 |
- 귀무 가설에 대한 타당성을 검정할 때, `p`-값을 이용한 방법은 다음과 같다.
① 귀무 가설 $H_{0}$ 와 대립 가설 $H_{1}$ 을 설정한다.
② 유의 수준 `α` 를 정한다.
③ 적당한 검정 통계량을 선택한다.
④ `p`-값을 구한다.
⑤ $p-값 \le α$ 이면 귀무 가설을 기각하고, $p-값 > α$ 이면 귀무 가설을 채택한다.
728x90
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모비율의 검정 (0) | 2022.12.01 |
|---|---|
| [확률과 통계] 모평균의 검정 (σ² : 미지) (0) | 2022.12.01 |
| [확률과 통계] 모평균의 검정(σ² : 기지) (0) | 2022.11.30 |
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
