모평균의 검정(σ² : 기지)
- 일반적으로 모평균에 대한 주장을 검정하기 위해 모집단은 정규 분포를 따른다고 가정한다.
- 그러면 모분산을 알고 있는 모평균에 대한 주장을 검정하기 위해 사용하는 확률 분포는 정규 분포이다.
- 특히 이 경우에 사용하는 검정 통계량은 표본 평균 $\overline{X}$ 의 표준화 확률 변수인 `Z` 이다.
- 이 페이지에서는 모분산이 알려져 있는 단일 정규 모집단의 모평균과 독립인 두 모집단의 모평균 차에 대한 귀무 가설을 검정하는 방법에 대해 살펴본다.
모평균에 대한 검정
모평균에 대한 양측 검정
- 모분산 $σ^{2}$ 이 알려진 정규 모집단에서 귀무 가설 $H_{0} : μ = μ_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : μ \ne μ_{0}$ 를 검정하는 방법을 살펴보자.
- 우선 귀무 가설의 진위를 결정하기 전까지 모평균이 $μ_{0}$ 라는 주장이 정당한 것으로 가정한다.
- 이러한 가정 아래에서 크기 `n` 인 표본을 임의로 추출하면 검정 통계량 `Z` 는 다음과 같이 표준 정규 분포를 따른다.
$$Z = \frac{\overline{X} - μ_{0}}{\frac{σ}{\sqrt{n}}} \; \sim \; N(0, \; 1)$$
- 한편, 미리 설정된 유의 수준 `α` 에 대한 검정 통계량 `Z` 에 대해 양쪽 꼬리 확률이 각각 `α / 2` 인 임계점은 $±z_{\frac{α}{2}}$ 이다.
기각과 채택
- 따라서 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같다.
$$Z \le -z_{\frac{α}{2}}, \quad Z \ge z_{\frac{\alpha}{2}}$$

검정통계량의 관찰값 $z_{0}$
- 그리고 검정 통계량의 관찰값 $z_{0}$ 는 다음과 같다.
$$z_{0} = \frac{\overline{x} - μ_{0}}{\frac{σ}{\sqrt{n}}}$$
- 이 때, 관찰값 $z_{0}$ 가 기각역 안에 놓이면 $H_{0}$ 를 기각하고, 채택역 안에 놓이면 $H_{0}$ 를 기각할 수 없다.
예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.32이었다.
(a) 귀무 가설과 대립 가설을 설정하라.
(b) 유의 수준 5%에서 기각역을 구하라.
(c) 검정 통계량의 관찰값을 구하라.
(d) 유의 수준 5%에서 귀무 가설을 검정하라.
(a)
귀무 가설은 $H_{0} : μ = 10$ 이고, 대립 가설은 $H_{1} : \mu \ne 10$ 이다.
(b)
유의 수준 $α = 0.05$ 인 양측 검정이므로 $z_{0.025} = 1.96$ 이다. 그리고 기각역은 $Z \le -1.96$ 또는 $Z \ge 1.96$ 이다.
(c)
$σ = 2, \; \overline{x} = 9.32, \; n = 36$ 이므로 검정 통계량의 관찰값은 $z_{0} = \frac{9.32 - 10}{2 / \sqrt{36}} = -2.04$ 이다.
(d)
$z_{0} = -2.04 \le -1.96$ 이므로 유의 수준 5%에서 귀무 가설을 기각한다.
`p`-값
- 모평균에 대한 양측 검정의 `p`-값은 다음과 같이 정의된다.
$$p-값 = P(Z < -|z_{0}|) + P(Z > |z_{0}|)$$
- 이 경우에 `p`-값은 다음과 같으며, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.
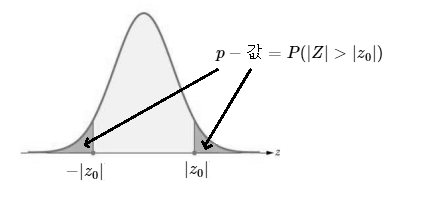
예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.32이었다. `p`-값을 구하고, $H_{0} : \mu = 10$ 을 검정하라.
검정 통계량의 관찰값이 $z_{0} = \frac{9.32 - 10}{2 / \sqrt{36}} = -2.04$ 이므로, `p`-값을 구하면 다음과 같다.
| $$p-값 = P(Z < -2.04) + P(Z > 2.04) = 2P(Z>2.04) = 2(1 - 0.9763) = 2 \times 0.0207 = 0.0414$$ |
$p-값 = 0.0414 \le \alpha = 0.05$ 이므로 귀무 가설을 기각한다.
모평균에 대한 상단측 검정
- 모분산 $σ^{2}$ 이 알려진 정규 모집단에서 귀무 가설 $H_{0} : \mu \le \mu_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : \mu > \mu_{0}$ 를 검정하는 방법을 살펴보자.
- 이 때, 미리 설정된 유의 수준 $\alpha$ 에 대한 검정 통계량 `Z` 에 대해 오른쪽 꼬리 확률이 $\alpha$ 인 임계점은 $z_{\alpha}$ 이다.
기각과 채택
- 그리고 검정 통계량은 `Z` 이고 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같다.
$$Z \ge z_{\alpha}$$
- 따라서 다음과 같이 관찰값 $z_{0}$ 가 기각역 안에 놓이면 $H_{0}$ 를 기각하고, 채택역 안에 놓이면 $H_{0}$ 를 기각할 수 없다.

예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.32이었다.
(a) 귀무 가설과 대립 가설을 설정하라.
(b) 유의 수준 1%에서 기각역을 구하라.
(c) 검정 통계량의 관찰값을 구하라.
(d) 유의 수준 1%에서 귀무 가설을 검정하라.
(a)
귀무 가설은 $H_{0} : μ \le 10$ 이고, 대립 가설은 $H_{1} : \mu > 10$ 이다.
(b)
유의 수준 $α = 0.01$ 인 상단측 검정이므로 $z_{0.01} = 2.33$ 이고, 기각역은 $Z \ge 2.33$ 이다.
(c)
$σ = 2, \; \overline{x} = 10.9, \; n = 36$ 이므로 검정 통계량의 관찰값은 $z_{0} = \frac{10.9 - 10}{2 / \sqrt{36}} = 2.7$ 이다.
(d)
$z_{0} = 2.7 \le 2.33$ 이므로 유의 수준 1%에서 귀무 가설을 기각한다.
`p`-값
- 모평균에 대한 상단측 검정의 `p`-값은 다음과 같이 정의된다.
$$p-값 = P(Z > z_{0})$$
- 이 경우에 `p`-값은 다음과 같으며, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.

예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.32이었다. `p`-값을 구하고, $H_{0} : \mu \le 10$ 을 검정하라.
검정 통계량의 관찰값이 $z_{0} = \frac{10.9 - 10}{2 / \sqrt{36}} = 2.7$ 이므로, `p`-값을 구하면 다음과 같다.
| $$p-값 = P(Z > 2.7) = 1 - P(Z \le 2.7) = 1 - 0.9965 = 0.0035$$ |
$p-값 = 0.0035 \le \alpha = 0.01$ 이므로 귀무 가설을 기각한다.
모평균에 대한 하단측 검정
- 모분산 $σ^{2}$ 이 알려진 정규 모집단에서 귀무 가설 $H_{0} : \mu \ge \mu_{0}$ 라는 주장과 이에 대립하는 대립 가설 $H_{1} : \mu < \mu_{0}$ 를 검정하는 방법을 살펴보자.
- 이 때, 미리 설정된 유의 수준 $\alpha$ 에 대한 검정 통계량 `Z` 에 대해 왼쪽 꼬리 확률이 $\alpha$ 인 임계점은 $-z_{\alpha}$ 이다.
기각과 채택
- 그리고 검정 통계량은 `Z` 이고 귀무 가설 $H_{0}$ 에 대한 기각역은 다음과 같다.
$$Z \le -z_{\alpha}$$
- 따라서 다음과 같이 관찰값 $z_{0}$ 가 기각역 안에 놓이면 $H_{0}$ 를 기각하고, 채택역 안에 놓이면 $H_{0}$ 를 기각할 수 없다.

예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.2이었다.
(a) 귀무 가설과 대립 가설을 설정하라.
(b) 유의 수준 1%에서 기각역을 구하라.
(c) 검정 통계량의 관찰값을 구하라.
(d) 유의 수준 1%에서 귀무 가설을 검정하라.
(a)
귀무 가설은 $H_{0} : μ \ge 10$ 이고, 대립 가설은 $H_{1} : \mu < 10$ 이다.
(b)
유의 수준 $α = 0.01$ 인 상단측 검정이므로 $z_{0.01} = 2.33$ 이고, 기각역은 $Z \le -2.33$ 이다.
(c)
$σ = 2, \; \overline{x} = 9.2, \; n = 36$ 이므로 검정 통계량의 관찰값은 $z_{0} = \frac{9.2 - 10}{2 / \sqrt{36}} = -2.4$ 이다.
(d)
$z_{0} = -2.4 \le -2.33$ 이므로 유의 수준 1%에서 귀무 가설을 기각한다.
`p`-값
- 모평균에 대한 상단측 검정의 `p`-값은 다음과 같이 정의된다.
$$p-값 = P(Z < z_{0})$$
- 이 경우에 `p`-값은 다음과 같으며, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.

예제 : 분산이 4인 정규 모집단에 대해 모평균이 10이라고 주장한다. 이를 검정하기 위해 크기 36인 표본을 추출한 결과, 표본 평균이 9.32이었다. `p`-값을 구하고, $H_{0} : \mu \ge 10$ 을 검정하라.
검정 통계량의 관찰값이 $$z_{0} = \frac{9.2 - 10}{2 / \sqrt{36}} = -2.4$ 이므로, `p`-값을 구하면 다음과 같다.
| $$p-값 = P(Z \le -2.4) = 1 - P(Z \le 2.4) = 1 - 0.9918 = 0.0082$$ |
$p-값 = 0.0082 \le \alpha = 0.01$ 이므로 귀무 가설을 기각한다.
모평균에 대한 검정 유형과 기각역 그리고 `p`-값 (종합)
| 검정 방법 \ 가설과 기각역 | 귀무 가설 $H_{0}$ | 대립 가설 $H_{1}$ | $H_{0}$ 의 기각역 | `p`-값 |
| 하단측 검정 | $\mu \ge \mu_{0}$ | $\mu < \mu_{0}$ | $Z \le -z_{\alpha}$ | $P(Z < z_{0})$ |
| 상단측 검정 | $\mu \le \mu_{0}$ | $\mu > \mu_{0}$ | $Z \ge z_{\alpha}$ | $P(Z > z_{0})$ |
| 양측 검정 | $\mu = \mu_{0}$ | $\mu \ne \mu_{0}$ | $|Z| \ge z_{\frac{α}{2}}$ | $P(|Z| > |z_{0}|)$ |
두 모평균 차에 대한 검정
- 독립인 두 모집단의 모분산 $\sigma_{1}^{2}$ 와 $\sigma_{2}^{2}$ 이 알려져 있고, 정규 분포 $N(\mu_{1}, \; \sigma_{1}^{2})$ 과 $N(\mu_{2}, \; \sigma_{2}^{2})$ 을 따른다고 하자.
- 그러면 두 모평균 차 $\mu_{1} - \mu_{2}$ 에 대해 다음과 같은 귀무 가설을 생각할 수 있다.
| $$H_{0} : \mu_{1} - \mu_{2} \ge d_{0}, \quad H_{0} : \mu_{1} - \mu_{2} = d_{0}, \quad H_{0} : \mu_{1} - \mu_{2} \le d_{0}$$ |
- 그리고 이에 대한 대립 가설은 각각 다음과 같다.
| $$H_{1} : \mu_{1} - \mu_{2} < d_{0}, \quad H_{1} : \mu_{1} - \mu_{2} \ne d_{0}, \quad H_{1} : \mu_{1} - \mu_{2} > d_{0}$$ |
- 한편, 크기가 `n` 과 `m` 인 두 표본의 표본 평균을 $\overline{X}$ 와 $\overline{Y}$ 라 하면, 각각 다음 정규 분포를 따른다.
| $$\overline{X} \sim N(\mu_{1}, \; \frac{\sigma_{1}^{2}}{n}), \quad \overline{Y} \sim N(\mu_{2}, \frac{\sigma_{2}^{2}}{m})$$ |
- 또한 두 표본 평균은 독립이므로 표본 평균의 차는 다음 정규 분포를 따른다.
| $$\overline{X} - \overline{Y} \sim N(\mu_{1} - \mu_{2}, \; \frac{\sigma_{1}^{2}}{n} + \frac{\sigma_{2}^{2}}{m})$$ |
- 그러므로 모분산 $\sigma_{1}^{2}$ 과 $\sigma_{2}^{2}$ 을 알고 독립인 두 정규 모집단에서 크기 `n` 과 `m` 인 표본을 추출하여 표본 평균을 각각 $\overline{X}, \; \overline{Y}$ 라 하면, 다음이 성립한다.
| $$Z = \frac{(\overline{X} - \overline{Y}) - (\mu_{1} - \mu_{2})}{\sqrt{(\frac{\sigma_{1}^{2}}{n}) + (\frac{\sigma_{2}^{2}}{m})}} \sim N(0, \; 1)$$ |
- 그러면 두 모평균에 대한 주장 $\mu_{1} - \mu_{2} = d_{0}$ 인 귀무 가설을 검정하기 위한 검정 통계량 `Z` 와 그에 대한 확률 분포는 다음과 같다.
$$Z = \frac{(\overline{X} - \overline{Y}) - (\mu_{1} - \mu_{2})}{\sqrt{(\frac{\sigma_{1}^{2}}{n}) + (\frac{\sigma_{2}^{2}}{m})}} \sim N(0, \; 1)$$
양측 검정
- 두 가설 $H_{0} : \mu_{1} - \mu_{2} = d_{0}, \; H_{1} : \mu_{1} - \mu_{2} \ne d_{0}$ 에 대해 유의 수준을 $\alpha$ 라 하자.
- 그러면 양쪽 꼬리 확률이 각각 $\frac{\alpha}{2}$ 가 되는 두 임계값이 $±z_{\frac{\alpha}{2}}$ 이므로 귀무 가설의 기각역은 다음과 같다.
$$Z \le -z_{\frac{\alpha}{2}}, \quad Z \ge z_{\frac{\alpha}{2}}$$
- 그러면 두 표본 평균의 관찰값 $\overline{x}$ 와 $\overline{y}$ 에 대해 검정 통계량의 관찰값은 다음과 같다.
$$z_{0} = \frac{(\overline{x} - \overline{y}) - d_{0}}{\sqrt{(\frac{\sigma_{1}^{2}}{n}) + (\frac{\sigma_{2}^{2}}{m})}} \sim N(0, \; 1)$$
- 따라서 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \le -z_{\frac{\alpha}{2}}$ 또는 $z_{0} \ge z_{\frac{\alpha}{2}}$ 이면 $H_{0}$ 를 기각하고 $-z_{\frac{\alpha}{2}} < z_{0} < z_{\frac{\alpha}{2}}$ 이면 $H_{0}$ 를 기각하지 못한다.
- 그리고 `p`-값은 단일 모집단의 경우와 동일하게 정의된다.
- 이 때, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.
상단측 검정
- 두 가설 $H_{0} : \mu_{1} - \mu_{2} \le d_{0}, \; H_{1} : \mu_{1} - \mu_{2} > d_{0}$ 에 대해 유의 수준을 $\alpha$ 라 하자.
- 그러면 오른쪽 꼬리 확률이 $\alpha$ 인 임계값 $z_{\alpha}$ 에 대해 기각역은 $Z \ge z_{\alpha}$ 이다.
- 이 때, 두 표본 평균의 관찰값 $\overline{x}$ 와 $\overline{y}$ 에 대한 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \ge z_{\alpha}$ 이면 $H_{0}$ 를 기각하고, $z_{0} < z_{\alpha}$ 이면 $H_{0}$ 를 기각하지 못한다.
- 또한, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.
하단측 검정
- 두 가설 $H_{0} : \mu_{1} - \mu_{2} \ge d_{0}, \; H_{1} : \mu_{1} - \mu_{2} < d_{0}$ 에 대해 유의 수준을 $\alpha$ 라 하자.
- 그러면 왼쪽 꼬리 확률이 $\alpha$ 인 임계값 $z_{\alpha}$ 에 대해 기각역은 $Z \le -z_{\alpha}$ 이다.
- 이 때, 두 표본 평균의 관찰값 $\overline{x}$ 와 $\overline{y}$ 에 대한 검정 통계량의 관찰값 $z_{0}$ 에 대해 $z_{0} \le -z_{\alpha}$ 이면 $H_{0}$ 를 기각하고, $z_{0} > z_{\alpha}$ 이면 $H_{0}$ 를 기각하지 못한다.
- 또한, $p-값 > \alpha$ 이면 $H_{0}$ 를 채택하고, $p-값 \le \alpha$ 이면 $H_{0}$ 를 기각한다.
두 모평균의 차에 대한 검정 유형과 기각역 그리고 `p`-값 (종합)
| 검정 방법 \ 가설과 기각역 | 귀무 가설 $H_{0}$ | 대립 가설 $H_{1}$ | $H_{0}$ 의 기각역 | `p`-값 |
| 하단측 검정 | $\mu_{1} - \mu_{2} \ge d_{0}$ | $\mu_{1} - \mu_{2} < d_{0}$ | $Z \le -z_{\alpha}$ | $P(Z < z_{0})$ |
| 상단측 검정 | $\mu_{1} - \mu_{2} \le d_{0}$ | $\mu_{1} - \mu_{2} > d_{0}$ | $Z \ge z_{\alpha}$ | $P(Z > z_{0})$ |
| 양측 검정 | $\mu_{1} - \mu_{2} = d_{0}$ | $\mu_{1} - \mu_{2} \ne d_{0}$ | $|Z| \ge z_{\frac{α}{2}}$ | $2[1 - P(Z < z_{0})]$ |
예제 : 두 모집단의 평균이 동일한지 알아보기 위해 표본 조사를 실시하여 다음을 얻었다. 이 때 `p`-값을 구하고, 평균이 동일한지 유의 수준 5%에서 검정하라.
| 표본 | 표본의 크기 | 표본 평균 | 모표준 편차 |
| A | 25 | 33.3 | 4.8 |
(1)
A와 B의 평균을 각각 $\mu_{1}, \mu_{2}$ 라 하면, 귀무 가설 $H_{0} : \mu_{1} = \mu_{2}$ 와 대립 가설 $H_{1} : \mu_{1} \ne \mu_{2}$ 를 설정한다. 즉, $H_{0} : \mu_{1} = \mu_{2}$ 와 $H_{1} : \mu_{1} \ne \mu_{2}$ 를 설정한다.
(2)
$\sigma_{1} = 4.8, \; \sigma_{2} = 5.4, \; n = 25, \; m = 36$ 이므로 검정 통계량을 구하면 다음과 같다.
| $$Z = \frac{\overline{X} - \overline{Y} - 0}{sqrt{(4.8^{2} / 25) + (5.4^{2} / 36)}} = \frac{\overline{X} - \overline{Y}}{1.3159}$$ |
(3)
$\overline{x} = 33.3, \; \overline{y} = 30.8$ 이므로 검정 통계량의 관찰값은 $z_{0} = \frac{33.3 - 30.8}{1.3159} ≒ 1.9$ 이다.
(4)
$z_{0} = 1.9$ 이므로 `p`-값과 유의 수준은 다음과 같다.
| $$p-값 = P(Z > 1.9) = 0.0287 < \alpha = 0.05$$ |
(5)
`p`-값이 유의 수준보다 작으므로 귀무 가설을 기각한다. 즉, 두 모평균이 동일하다는 주장은 근거가 없다.
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모비율의 검정 (0) | 2022.12.01 |
|---|---|
| [확률과 통계] 모평균의 검정 (σ² : 미지) (0) | 2022.12.01 |
| [확률과 통계] 통계적 가설 검정 (0) | 2022.11.28 |
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
