◀️ 🌱 April 🌱 ▶️
일	월	목	금	토
		0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0

[이산 수학] 관계의 성질

2022. 10. 31. 00:11

728x90

관계의 성질

하나의 집합에 대한 관계의 경우, 순서쌍 원소의 구성에 따라 관계의 성질을 판별할 수 있다.
관계의 성질에는 반사, 비반사, 대칭, 반대칭, 추이 5가지가 있다.

반사 관계와 비반사 관계

반사 관계(Reflexive Relation)

집합 $A$ $A$ 에 대한 관계 $R$ 이 있을 때, 모든 $a ∈ A$ 에 대해 $(a, a) ∈ R$ 인 관계 ( $Δ_{A} = \{ (a, a) \; | \; a ∈ A \}$ )

비반사 관계(Irreflexive Relation)

집합 $A$ $A$ 에 대한 관계 $R$ 이 있을 때, 모든 $a ∈ A$ 에 대해 $(a, a) \not ∈ R$ 인 관계

집합 A $A$ 에 대한 관계 R $R$ 이 반사 관계이려면, 집합 A $A$ 에 포함되는 모든 원소 a $a$ 에 대해 자기 자신과 대응하는 순서쌍 (a,a) $(a, a)$ 가 관계 R $R$ 에 포함되어 있어야 한다.
- 즉, 집합 $A$ $A$ 의 원소 중 하나에 대해서라도 자기 자신과 대응하는 순서쌍이 관계 $R$ $R$ 에 포함되지 않는다면 관계 $R$ $R$ 은 반사 관계가 아니다.
반면, 관계 R $R$ 을 만드는 집합 A $A$ 의 모든 원소 a $a$ 에 대해 자기 자신과 대응하는 순서쌍 (a,a) $(a, a)$ 가 관계 R $R$ 에 하나도 포함되지 않으면 관계 R $R$ 은 비반사 관계이다.
- 즉, 집합 $A$ $A$ 의 원소 중 하나에 대해서라도 자기 자신과 대응하는 순서쌍이 관계 $R$ $R$ 에 포함된다면 관계 $R$ $R$ 은 비반사 관계가 아니다.

예

$A = \{ 1, 2, 3 \}$ 에 대하여 $A$ $A$ 에서 $A$ $A$ 로 가는 다음과 같은 관계가 있다고 가정하자.

$R_{1} = \{(1, 1), (1, 2), (2, 2), (2, 3), (3, 3) \} \\ R_{2} = \{(1, 1), (2, 1), (2, 2), (3, 1), (3, 2) \} \\ R_{3} = \{(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) \}$

관계 $R_{1}$ 의 경우, 집합 $A$ 에 포함된 모든 원소 1, 2, 3에 대해 자기 자신과 대응하는 순서쌍 $(1, 1), (2, 2), (3, 3)$ 을 원소로 포함한다. 그러므로 관계 $R_{1}$ 은 반사 관계이다.
반면, 관계 R2 는 집합 A 의 원소 중 3에 대해 자기 자신과 대응하는 순서쌍 (3,3) 을 포함하지 않고, 관계 R3 는 집합 A 의 모든 원소에 대해 자기 자신과 대응하는 순서쌍을 포함하지 않는다.
- 이렇게 관계 $R_{2}$ 와 $R_{3}$ 처럼 관계를 만드는 집합의 원소 중 하나라도 자기 자신과 대응하는 순서쌍을 관계에 포함하지 않으면 반사 관계가 아니다.
다만, 관계 $R_{3}$ 의 경우, 집합 $A$ 의 모든 원소에 대해 자기 자신과 대응하는 순서쌍을 하나도 포함하지 않으므로 비반사 관계이다.
그러나 관계 $R_{1}$ 과 같이 집합 $A$ 의 모든 원소에 대해 자기 자신과 대응하는 순서쌍을 갖거나, 관계 $R_{2}$ 와 같이 집합 $A$ 의 원소 중 일부에 대해서만 자기 자신과 대응하는 순서쌍을 갖는 관계는 비반사 관계가 아니다.
정리하면, 관계 $R_{1}$ 은 반사 관계이고, 관계 $R_{3}$ 는 비반사 관계이며, 관계 $R_{2}$ 는 반사 관계도 비반사 관계도 아니다.

반사 관계의 경우, 다음 그림처럼 관계 행렬로 표현하면 행렬의 주대각 원소가 모두 1이고, 방향 그래프로 표현하면 모든 꼭지점이 루프를 갖는다.

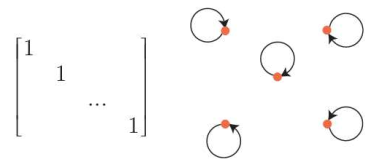
비반사 관계의 경우, 다음 그림처럼 관계 행렬의 주대각 원소는 모두 0이고, 방향 그래프의 모든 꼭짓점은 루프를 갖지 않는다.

반사 관계 $R_{1}$ 을 관계 행렬과 방향 그래프로 표현하면 다음과 같다.

$\quad \quad \quad \quad \begin{matrix} 1 & 2 & 3 \end{matrix} \\ M_{R_{1}} = \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}$

반사 관계 $R_{3}$ 을 관계 행렬과 방향 그래프로 표현하면 다음과 같다.

$\quad \quad \quad \quad \begin{matrix} 1 & 2 & 3 \end{matrix} \\ M_{R_{1}} = \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \end{bmatrix}$

반사 관계도, 비반사 관계도 아닌 관계의 관계 행렬의 주대각 원소는 0과 1이 섞여 있으며, 방향 그래프는 루프가 있는 꼭짓점과 루프가 없는 꼭짓점이 섞여 있다.

대칭 관계와 반대칭 관계

대칭 관계(Symmetric Relation)

집합 $A$ 에 대한 관계 $R$ 이 있을 때, 어떤 $a, b ∈ A$ 애 대해 $(a, b) ∈ R$ 이면 $(b, a) ∈ R$ 인 관계

반대칭 관계(Antisymmetric Relation)

집합 $A$ 에 대한 관계 $R$ 이 있을 때, 어떤 $a, b ∈ A$ 애 대해 $(a, b) ∈ R$ 이고 $(b, a) ∈ R$ 이면 $a = b$ 인 관계

관계 R 이 대칭 관계이려면 어떤 순서쌍 (a,b) 가 관계 R 에 포함될 때 (b,a) 도 관계 R 에 포함되어야 한다.
- 이 때, $a = b$ 이든, $a ≠ b$ 이든 상관없다.
반대칭 관계의 경우에는 $(a, b)$ 가 관계 $R$ 에 포함될 때 $a ≠ b$ 라면, $(b, a)$ 가 관계 $R$ 에 포함되지 않아야 한다.

예

$A = \{ 1, 2, 3 \}$ 에 대해 다음과 같은 관계가 있다고 가정하자.

$R_{1} = \{(1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) \} \\ R_{2} = \{(1, 1), (1, 2), (2, 3), (3, 1) \} \\ R_{3} = \{(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) \} \\ R_{4} = \{(1, 1), (3, 3) \}$

관계 R1 에 포함된 순서쌍을 살펴보면 다음과 같다.
- $(1, 1) ∈ R_{1}$ 일 때, $1 = 1$ 이고 $(1, 1) ∈ R_{1}$
- $(1, 2) ∈ R_{1}$ 일 때, $1 ≠ 2$ 이고 $(2, 1) ∈ R_{1}$
- $(1, 3) ∈ R_{1}$ 일 때, $1 ≠ 3$ 이고 $(3, 1) ∈ R_{1}$
- $(2, 1) ∈ R_{1}$ 일 때, $2 ≠ 1$ 이고 $(1, 2) ∈ R_{1}$
- $(2, 3) ∈ R_{1}$ 일 때, $2 ≠ 3$ 이고 $(3, 2) ∈ R_{1}$
- $(3, 1) ∈ R_{1}$ 일 때, $3 ≠ 1$ 이고 $(1, 3) ∈ R_{1}$
- $(3, 2) ∈ R_{1}$ 일 때, $3 ≠ 2$ 이고 $(2, 3) ∈ R_{1}$
위에서 알 수 있듯이 $a = b$ 이든, $a ≠ b$ 이든 상관 없이 관계 $R_{1}$ 에 포함된 모든 순서쌍 $(a, b)$ 에 대해 $(b, a)$ 가 관계 $R_{1}$ 에 포함되므로 관계 $R_{1}$ 은 대칭 관계이다.
반면, $(1, 2), (2, 1)$ 처럼 $a ≠ b$ 인데 순서쌍 $(a, b)$ 와 $(b, a)$ 가 모두 $R_{1}$ 에 포함되는 경우가 있으므로 관계 $R_{1}$ 은 반대칭 관계가 아니다.
정리하면 관계 $R_{1}$ 은 대칭 관계이지만 반대칭 관계는 아니다.

관계 R2 에 포함된 순서쌍을 살펴보면 다음과 같다.
- $(1, 1) ∈ R_{2}$ 일 때, $1 = 1$ 이고 $(1, 1) ∈ R_{2}$
- $(1, 2) ∈ R_{2}$ 일 때, $1 ≠ 2$ 이고 $(2, 1) \not ∈ R_{2}$
- $(2, 3) ∈ R_{2}$ 일 때, $2 ≠ 3$ 이고 $(3, 2) \not ∈ R_{2}$
- $(3, 1) ∈ R_{2}$ 일 때, $3 ≠ 1$ 이고 $(1, 3) \not ∈ R_{2}$
관계 $R_{2}$ 에 포함된 순서쌍 중 $a ≠ b$ 인 $(a, b)$ 에 대해서는 $(b, a)$ 가 존재하지 않고, $(1, 1)$ 처럼 $a = b$ 인 순서쌍은 $R_{2}$ 에 포함되므로 관계 $R_{2}$ 는 대칭 관계는 아니지만 반대칭 관계이다.
관계 $R_{2}$ 와 같이 반대칭 관계이려면 $a ≠ b$ 인 $(a, b)$ 에 대해서는 $(b, a)$ 가 존재하지 않아야 한다.

관계 R3 에 포함된 순서쌍을 살펴보면 다음과 같다.
- $(1, 2) ∈ R_{3}$ 일 때, $1 ≠ 2$ 이고 $(2, 1) ∈ R_{3}$
- $(1, 3) ∈ R_{3}$ 일 때, $1 ≠ 3$ 이고 $(3, 1) ∈ R_{3}$
- $(2, 1) ∈ R_{3}$ 일 때, $2 ≠ 1$ 이고 $(1, 2) ∈ R_{3}$
- $(3, 1) ∈ R_{3}$ 일 때, $3 ≠ 1$ 이고 $(1, 3) ∈ R_{3}$
- $(3, 2) ∈ R_{3}$ 일 때, $3 ≠ 2$ 이고 $(2, 3) \not ∈ R_{3}$
관계 $R_{3}$ 에 포함된 순서쌍은 모두 $a ≠ b$ 이다.
관계 $R_{3}$ 의 순서쌍 $(1, 2), (1, 3), (2, 1), (3, 1)$ 은 $(a, b)$ 에 대해 $(b, a)$ 가 관계 $R_{3}$ 에 포함되지만, $(3, 2)$ 의 경우 $(2, 3)$ 이 관계 $R_{3}$ 에 포함되지 않는다. 그러므로 관계 $R_{3}$ 는 대칭 관계가 아니다.
또한 $(1, 2), (1, 3)$ 은 이에 대칭되는 $(2, 1), (3, 1)$ 이 관계 $R_{3}$ 에 포함되므로 반대칭 관계도 아니다.
정리하면 관계 $R_{3}$ 는 대칭 관계도 아니고 반대칭 관계도 아니다.

관계 $R_{4}$ 는 $a = b$ 이든 $a ≠ b$ 이든 상관없이 모든 순서쌍 $(a, b)$ 에 대해 $(b, a)$ 를 포함하므로 대칭 관계임을 알 수 있고, 두 순서쌍 $(1, 1), (3, 3)$ 모두 $a = b$ 이므로 반대칭 관계임을 알 수 있다.
그러므로 관계 $R_{4}$ 는 대칭 관계이면서 반대칭 관계이다.

위에서 볼 수 있듯이, 대칭 관계가 아니라고 해서 반대칭 관계이거나, 반대칭 관계가 아니라고 해서 대칭 관계인 것은 아니다.
- 대칭 관계와 반대칭 관계는 양립 관계가 아니다.
- 관계 $R_{3}$ 처럼 대칭 관계도, 반대칭 관계도 아닐 수 있고, $R_{4}$ 처럼 둘 다일 수도 있다.
대칭 관계를 관계 행렬이나 방향 그래프로 표현하면 다음과 같다.
- 관계 행렬은 주대각 원소를 기준으로 서로 마주보는 원소가 같은 값인 형태이다.
- 방향 그래프는 루프가 존재하거나, 두 점 사이에 반드시 양방향 화살표가 존재해야 한다.

대칭 관계 $R_{1}$ 을 관계 행렬과 방향 그래프로 표현하면 다음과 같다.

$\quad \quad \quad \quad \begin{matrix} 1 & 2 & 3 \end{matrix} \\ M_{R_{1}} = \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{bmatrix}$

반대칭 관계를 관계 행렬이나 방향 그래프로 표현하면 다음과 같다.
- 관계 행렬은 주대각 원소를 기준으로 대칭으로 마주보는 원소가 모두 0이거나 서로 달라야 한다.
  - 어떤 원소와 그에 대칭으로 대응하는 원소가 모두 0이면 관계에 해당 순서쌍들이 포함되지 않음을 의미하므로 상관 없지만, 관계 행렬에서 어떤 원소가 1이면 이 원소와 대칭으로 마주보는 원소는 0이어야 반대칭 관계로 판단할 수 있다.
- 방향 그래프는 단방향 화살표나 루프만 존재해야 한다.

반대칭 관계 $R_{2}$ 를 관계 행렬과 방향 그래프로 표현하면 다음과 같다.

$\quad \quad \quad \quad \begin{matrix} 1 & 2 & 3 \end{matrix} \\ M_{R_{1}} = \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \begin{bmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}$

추이 관계

추이 관계(Transitive Relation)

집합 $A$ 에 대한 관계 $R$ 이 있을 때, 어떤 $a, b, c ∈ A$ 에 대해 $(a, b) ∈ R$ 이고, $(b, c) ∈ R$ 이면 $(a, c) ∈ R$ 인 관계

추이 관계인지 확인하려면 관계 $R$ 에 포함된 모든 순서쌍을 살펴보아야 한다.

예

$A = \{ 1, 2, 3 \}$ 에 대해 다음과 같은 관계가 있다고 가정하자.

$R_{1} = \{(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3) \} \\ R_{2} = \{(1, 2), (1, 3), (2, 3), (3, 2) \}$

관계 $R_{1}$ 에서 첫 번째 순서쌍 $(1, 1)$ 의 뒤의 원소 1을 앞의 원소로 갖는 순서쌍은 $(1, 1), (1, 2), (1, 3)$ 이다.
이 중, (1,1) 에서 앞의 원소 1을 앞의 원소로 하고, (1,2) 에서 뒤의 원소 2를 뒤의 원소로 하는 순서쌍 (1,2) 가 관계 R1 에 있음을 확인할 수 있다.
- $(1, 1) ∈ R_{1}$ 이고, $(1, 2) ∈ R_{1}$ 일 때, $(1, 2) ∈ R_{1}$
이러한 방식으로 관계 R1 에 포함된 모든 순서쌍을 살펴보면 다음과 같다.
- (1) $(1, 1)$ 의 뒤의 원소 1을 앞의 원소로 하는 순서쌍 : (1,1),(1,2),(1,3)
  - $(1, 1) ∈ R_{1}$ 이고, $(1, 1) ∈ R_{1}$ 일 때, $(1, 1) ∈ R_{1}$
  - $(1, 1) ∈ R_{1}$ 이고, $(1, 2) ∈ R_{1}$ 일 때, $(1, 2) ∈ R_{1}$
  - $(1, 1) ∈ R_{1}$ 이고, $(1, 3) ∈ R_{1}$ 일 때, $(1, 3) ∈ R_{1}$
- (2) $(1, 2)$ 의 뒤의 원소 2를 앞의 원소로 하는 순서쌍 : $(2, 1), (2, 2), (2, 3)$
  - $(1, 2) ∈ R_{1}$ 이고, $(2, 1) ∈ R_{1}$ 일 때, $(1, 1) ∈ R_{1}$
  - $(1, 2) ∈ R_{1}$ 이고, $(2, 2) ∈ R_{1}$ 일 때, $(1, 2) ∈ R_{1}$
  - $(1, 2) ∈ R_{1}$ 이고, $(2, 3) ∈ R_{1}$ 일 때, $(1, 3) ∈ R_{1}$
- (3) $(1, 3)$ 의 뒤의 원소 3을 앞의 원소로 하는 순서쌍은 $R_{1}$ 에 없으므로 추이 관계를 고려할 필요가 없다.
- (4) $(2, 1)$ 의 뒤의 원소 1을 앞의 원소로 하는 순서쌍 : $(1, 1), (1, 2), (1, 3)$
  - $(2, 1) ∈ R_{1}$ 이고, $(1, 1) ∈ R_{1}$ 일 때, $(2, 1) ∈ R_{1}$
  - $(2, 1) ∈ R_{1}$ 이고, $(1, 2) ∈ R_{1}$ 일 때, $(2, 2) ∈ R_{1}$
  - $(2, 1) ∈ R_{1}$ 이고, $(1, 3) ∈ R_{1}$ 일 때, $(2, 3) ∈ R_{1}$
- (5) $(2, 2)$ 의 뒤의 원소 2를 앞의 원소로 하는 순서쌍 : $(2, 1), (2, 2), (2, 3)$
  - $(2, 2) ∈ R_{1}$ 이고, $(2, 1) ∈ R_{1}$ 일 때, $(2, 1) ∈ R_{1}$
  - $(2, 2) ∈ R_{1}$ 이고, $(2, 2) ∈ R_{1}$ 일 때, $(2, 2) ∈ R_{1}$
  - $(2, 2) ∈ R_{1}$ 이고, $(2, 3) ∈ R_{1}$ 일 때, $(2, 3) ∈ R_{1}$
- (6) $(2, 3)$ 의 뒤의 원소 3을 앞의 원소로 하는 순서쌍은 $R_{1}$ 에 없으므로 추이 관계를 고려할 필요가 없다.
그러므로 관계 $R_{1}$ 에 포함되는 순서쌍 중 추이 관계를 고려할 필요가 없는 $(1, 3), (2, 3)$ 을 제외한 모든 순서쌍 사이에 추이 관계가 성립하므로, 관계 $R_{1}$ 은 추이 관계이다.
- 추이 관계를 고려할 필요가 없는 순서쌍은 그 순서쌍의 뒤의 원소를 앞의 원소로 하는 순서쌍이 없는 경우를 말한다.
  - 예) $R = \{ (1, 3) \}$ 과 같은 관계가 있을 경우, 관계 $R$ 에 포함된 순서쌍 $(1, 3)$ 은 앞의 원소가 3인 다른 순서쌍이 관계 $R$ 에 없으므로 추이 관계를 고려할 필요가 없는 순서쌍이다. 그러므로 관계 $R$ 은 추이 관계가 성립한다고 할 수 있다.

R2 에 포함된 모든 순서쌍을 살펴보면 다음과 같다.
- (1) $(1, 2)$ 의 뒤의 원소 2를 앞의 원소로 하는 순서쌍 : (2,3)
  - $(1, 2) ∈ R_{2}$ 이고, $(2, 3) ∈ R_{2}$ 일 때, $(1, 3) ∈ R_{2}$
- (2) $(1, 3)$ 의 뒤의 원소 3을 앞의 원소로 하는 순서쌍 : (3,2)
  - $(1, 3) ∈ R_{2}$ 이고, $(3, 2) ∈ R_{2}$ 일 때, $(1, 2) ∈ R_{2}$
- (3) $(2, 3)$ 의 뒤의 원소 3을 앞의 원소로 하는 순서쌍 : (3,2)
  - $(2, 3) ∈ R_{2}$ 이고, $(3, 2) ∈ R_{2}$ 일 때, $(2, 2) \not ∈ R_{2}$
여기서 (2,3) 과 (3,2) 는 관계 R2 에 포함되지만 두 순서쌍으로 인해 만들어지는 순서쌍 (2,2) 는 관계 R2 에 포함되지 않는다.
- 그러므로 관계 $R_{2}$ 는 추이 관계가 아니다.
관계 $R_{2}$ 처럼 하나의 순서쌍이라도 추이 관계가 성립하지 않는다면 그 관계는 추이 관계가 아니다.

집합 $A$ 에 대한 관계 $R = \varnothing$ 의 성질

집합 A 의 모든 원소 a∈A 에 대해 (a,a)∉R
- ∴ $R$ 은 반사 관계가 아니고 비반사 관계이다.
관계 R 을 관계 행렬로 표현하면 주대각 원소를 기준으로 대칭으로 마주보는 원소가 모두 0으로 서로 대응한다.
- $\displaystyle M_{R} = \begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 0 \end{bmatrix}$
- ∴ $R$ 은 대칭 관계이고 반대칭 관계이다.
관계 R 은 추이 관계를 고려할 원소를 포함하지 않는다.
- ∴ $R$ 은 추이 관계이다.

728x90

저작자표시 비영리 변경금지

'Mathematics > 이산 수학' 카테고리의 다른 글

[이산 수학] 함수의 개념 (0)	2022.11.14
[이산 수학] 동치 관계와 부분 순서 관계 (0)	2022.11.06
[이산 수학] 관계의 폐포 (0)	2022.11.06
[이산 수학] 합성 관계 (0)	2022.10.31
[이산 수학] 관계의 표현 (0)	2022.10.29
[이산 수학] 관계의 개념 (0)	2022.10.29
[이산 수학] 집합의 분할 (0)	2022.10.22
[이산 수학] 집합의 대수 법칙 (0)	2022.10.22

Per ardua ad astra."Hello, World!" 🤖

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Per ardua ad astra.

"Hello, World!"

[이산 수학] 관계의 성질

관계의 성질