728x90
728x90
문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
예제 입력 1
3 16
예제 출력 1
3
5
7
11
13
알고리즘 분류
- 수학
- 정수론
- 소수 판정
- 에라토스테네스의 체
문제 출처
https://www.acmicpc.net/problem/1929
1929번: 소수 구하기
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
www.acmicpc.net
문제 해결 방법
- 기본적인 소수 판별 알고리즘으로는 시간 초과 문제로 인해 해결할 수 없는 문제였다.
- 그래서 다음의 2가지 방법을 이용하여 빠르게 소수 판별을 하도록 하였다.
- 에라토스테네스의 체
- 제곱근을 이용하여 문제 해결하기 (관련 내용 바로가기)
- 우선, 크기가 N + 1인 배열(nums[N + 1])을 생성한 후, i 인덱스의 위치에 i의 값을 넣어 채운다.
- 에라토스테네스의 체는 숫자 2부터 시작하므로, 배열의 첫 번째와 두 번째 인덱스는 0으로 채운다. (nums[0] = nums[1] = 0)
- 에라토스테네스의 체 알고리즘을 거쳐 소수로 판별되지 않은 배열의 요소를 0으로 바꾼 후, 최종적으로 요소가 0이 아닌 배열의 인덱스를 출력하도록 한다.
코드
#include <iostream>
#include <cmath>
using namespace std;
int M, N, k, *nums;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> M >> N;
nums = new int[N + 1];
// 배열 내부 채워넣기 (2부터 ~ )
nums[0] = nums[1] = 0;
for (int i = 2; i <= N; i++) {
nums[i] = i;
}
k = sqrt(N); // 제곱근을 이용하여 소수 판별하기
// 에라토스테네스의 체 알고리즘을 이용하여 문제 해결하기
for (int i = 2; i <= k; i++) {
if (nums[i] == 0) {
continue; // 이미 소수가 아닌 것으로 판정됐을 경우 넘어가기
}
for (int j = i * 2; j <= N; j += i) {
if (nums[j] == 0) {
continue; // 이미 소수가 아닌 것으로 판정됐을 경우 넘어가기
}
else {
nums[j] = 0;
}
}
}
// 결과 출력하기
for (int i = M; i <= N; i++) {
if (nums[i] != 0) {
cout << i << '\n';
}
}
delete[] nums;
return 0;
}
채점 결과

참고
- [단계별로 풀어보기] > [기본 수학 2]
- 실버III
에라토스테네스의 체(Sieve of Eratosthenes)
개념
- 2 이상의 구하고자 하는 범위 내에 존재하는 자연수를 모두 나열한 뒤, 2의 배수부터 3의 배수, 4의 배수, ... 등 차례로 그 수의 배수들을 지워나간다.
- 이러한 과정을 마친 후 남아 있는 수들이 소수(Prime Number)이다.
| 단계 0 | 단계 1 |
2부터 50까지 범위 내에 존재하는 소수를 구해본다.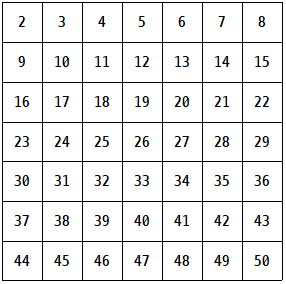 |
2를 제외한 2의 배수를 모두 제외한다. |
| 단계 2 | 단계 3 |
3을 제외한 3의 배수를 모두 제외한다. |
4의 배수는 앞서 1단계에서 모두 제외되었으므로, 5를 제외한 5의 배수를 모두 제외한다.  |
| 단계 4 | |
앞선 단계들과 마찬가지로 아직 지워지지 않은 7의 배수, 11의 배수, ... 등을 지워나가면 최종적으로 소수들만 남게 된다.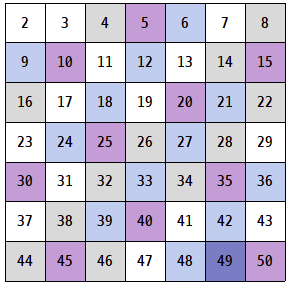 |
따라서 2와 50사이에 존재하는 소수는 다음과 같다. [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47] |
알고리즘
/* 2 이상 N 이하의 소수 구하기 */
int sieve[N];
sieve[0] = sieve[1] = 0;
for (int i = 2; i <= N; i++) {
sieve[i] = i;
}
for (int i = 2; i <= N; i++) {
if (sieve[i] == 0) { // 이미 수가 지워진 경우 넘어간다.
continue;
}
for (int j = i * 2; j <= N; j += i) { // 단계 1, 2, 3, ... 의 과정
if (nums[j] == 0) { // 이미 수가 지워진 경우 넘어간다.
continue;
}
else {
nums[j] = 0; // 수를 지운다.
}
}
}
for (int i = 2; i <= N; i++) {
if (nums[i] != 0) { // 배열의 요소값이 0이 아닌(지워지지 않은)
cout << i << '\n' // 인덱스를 출력한다.
}
}
728x90
728x90
'Problem Solving > BOJ' 카테고리의 다른 글
| [BOJ-2559][C++] 수열 (0) | 2022.10.26 |
|---|---|
| [BOJ-11659] 구간 합 구하기 4 (0) | 2022.10.26 |
| [BOJ-9020][C++] 골드바흐의 추측 (0) | 2022.10.25 |
| [BOJ-4948][C++] 베르트랑 공준 (0) | 2022.10.25 |
| [BOJ-11653][C++] 소인수분해 (0) | 2022.10.25 |
| [BOJ-2581][C++] 소수 (0) | 2022.10.25 |
| [BOJ-1978][C++] 소수 찾기 (0) | 2022.10.25 |
| [BOJ-2830][C++] 설탕 배달 (0) | 2022.10.24 |
