문제
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다.
이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼프가 1850년에 증명했다.
예를 들어, 10보다 크고, 20보다 작거나 같은 소수는 4개가 있다. (11, 13, 17, 19) 또, 14보다 크고, 28보다 작거나 같은 소수는 3개가 있다. (17,19, 23)
자연수 n이 주어졌을 때, n보다 크고, 2n보다 작거나 같은 소수의 개수를 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 케이스는 n을 포함하는 한 줄로 이루어져 있다.
입력의 마지막에는 0이 주어진다.
출력
각 테스트 케이스에 대해서, n보다 크고, 2n보다 작거나 같은 소수의 개수를 출력한다.
제한
- 1 ≤ n ≤ 123,456
예제 입력 1
1
10
13
100
1000
10000
100000
0
예제 출력 1
1
4
3
21
135
1033
8392
출처
ICPC > Regionals > Asia Pacific > Japan > Japan Domestic Contest > 2011 Japan Domestic Contest A번
알고리즘 분류
- 수학
- 정수론
- 소수 판정
- 에라토스테네스의 체
문제 출처
https://www.acmicpc.net/problem/4948
4948번: 베르트랑 공준
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다. 이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼
www.acmicpc.net
문제 해결 방법
- 소수 판별을 위한 다음의 2가지 방법을 이용하여 빠르게 소수 판별을 하도록 하였다.
- 에라토스테네스의 체
- 제곱근을 이용하여 문제 해결하기 (관련 내용 바로가기)
- 우선, 크기가 N + 1인 배열(nums[N + 1])을 생성한 후, i 인덱스의 위치에 i의 값을 넣어 채운다.
- 에라토스테네스의 체는 숫자 2부터 시작하므로, 배열의 첫 번째와 두 번째 인덱스는 0으로 채운다. (nums[0] = nums[1] = 0)
- 에라토스테네스의 체 알고리즘을 거쳐 소수로 판별되지 않은 배열의 요소를 0으로 바꾼 후, 최종적으로 요소가 0이 아닌 배열의 인덱스의 개수를 cnt 변수에 넣어 출력하도록 한다.
코드
#include <iostream>
#include <cmath>
using namespace std;
int n, k, *nums, cnt;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
while (1) {
cin >> n;
if (n == 0) {
break;
}
k = sqrt(2 * n);
nums = new int[(2 * n) + 1];
nums[0] = nums[1] = 0;
for (int i = 2; i <= (2 * n); i++) {
nums[i] = i;
}
// 에라토스테네스의 체 알고리즘
for (int i = 2; i <= k; i++) {
if (nums[i] == 0) continue;
for (int j = i * 2; j <= (2 * n); j += i) {
if (nums[j] == 0) continue;
else nums[j] = 0;
}
}
cnt = 0;
for (int i = n + 1; i <= (n * 2); i++) { // n보다 크고 2n보다 작거나 같은
if (nums[i] != 0) {
cnt++;
}
}
cout << cnt << '\n';
delete[] nums;
}
return 0;
}
채점 결과

참고
- [단계별로 풀어보기] > [기본 수학 2]
- 실버III
에라토스테네스의 체(Sieve of Eratosthenes)
개념
- 2 이상의 구하고자 하는 범위 내에 존재하는 자연수를 모두 나열한 뒤, 2의 배수부터 3의 배수, 4의 배수, ... 등 차례로 그 수의 배수들을 지워나간다.
- 이러한 과정을 마친 후 남아 있는 수들이 소수(Prime Number)이다.
| 단계 0 | 단계 1 |
2부터 50까지 범위 내에 존재하는 소수를 구해본다. |
2를 제외한 2의 배수를 모두 제외한다. |
| 단계 2 | 단계 3 |
3을 제외한 3의 배수를 모두 제외한다. |
4의 배수는 앞서 1단계에서 모두 제외되었으므로, 5를 제외한 5의 배수를 모두 제외한다. 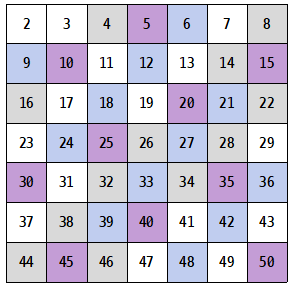 |
| 단계 4 | |
앞선 단계들과 마찬가지로 아직 지워지지 않은 7의 배수, 11의 배수, ... 등을 지워나가면 최종적으로 소수들만 남게 된다. |
따라서 2와 50사이에 존재하는 소수는 다음과 같다. [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47] |
알고리즘
/* 2 이상 N 이하의 소수 구하기 */
int sieve[N];
sieve[0] = sieve[1] = 0;
for (int i = 2; i <= N; i++) {
sieve[i] = i;
}
for (int i = 2; i <= N; i++) {
if (sieve[i] == 0) { // 이미 수가 지워진 경우 넘어간다.
continue;
}
for (int j = i * 2; j <= N; j += i) { // 단계 1, 2, 3, ... 의 과정
if (nums[j] == 0) { // 이미 수가 지워진 경우 넘어간다.
continue;
}
else {
nums[j] = 0; // 수를 지운다.
}
}
}
for (int i = 2; i <= N; i++) {
if (nums[i] != 0) { // 배열의 요소값이 0이 아닌(지워지지 않은)
cout << i << '\n' // 인덱스를 출력한다.
}
}
베르트랑 공준(Bertrand's Postulate) / 베르트랑-체비쇼프 정리(Bertrand-Chebyshev Theorem) / 베르트랑 가설(Bertrand's Theory)
개념
- 정수론에서 소수들의 분포에 관한 정리로, 두 자연수 `n` 과 `2n` 사이에 적어도 하나의 소수가 존재한다는 이론이다.
정의
임의의 정수 $n ≥ 2$ 에 대하여, $n < p < 2n$ 인 소수 $p$ 가 항상 존재한다.
역사
프랑스의 수학자 조제프 베르트랑(Joseph Louis François Bertrand)이 1845년에 처음으로 추측하여 베르트랑 추측이라는 이름을 얻었다. 베르트랑이 처음으로 이 명제에 대한 추측을 내놓았을 때 그는 3백만보다 작은 모든 자연수에 대한 계산을 덧붙였으나 증명은 하지 못했다.
5년 뒤 1850년에 파프누티 체비쇼프가 이 명제를 완전하게 증명하였다. 그럼에도 불구하고 관례적으로 '베르트랑 공준'이라 불린다. 1919년에 스리니바사 라마누잔이 감마 함수를 사용하여 더 간단한 증명을 발표하였고, 1932년에 에르되시 팔은 이항 계수와 체비쇼프 함수를 사용한, 라마누잔 증명보다 더 간단한 증명을 발표하였다.
참고 사이트
베르트랑 공준 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
'Problem Solving > BOJ' 카테고리의 다른 글
| [BOJ-10989][C++] 수 정렬하기 3 (0) | 2022.10.27 |
|---|---|
| [BOJ-2559][C++] 수열 (0) | 2022.10.26 |
| [BOJ-11659] 구간 합 구하기 4 (0) | 2022.10.26 |
| [BOJ-9020][C++] 골드바흐의 추측 (0) | 2022.10.25 |
| [BOJ-1929][C++] 소수 구하기 (0) | 2022.10.25 |
| [BOJ-11653][C++] 소인수분해 (0) | 2022.10.25 |
| [BOJ-2581][C++] 소수 (0) | 2022.10.25 |
| [BOJ-1978][C++] 소수 찾기 (0) | 2022.10.25 |
