728x90
728x90
수의 체계
수의 체계
- 수의 체계는 다음과 같이 표현할 수 있다.
 |
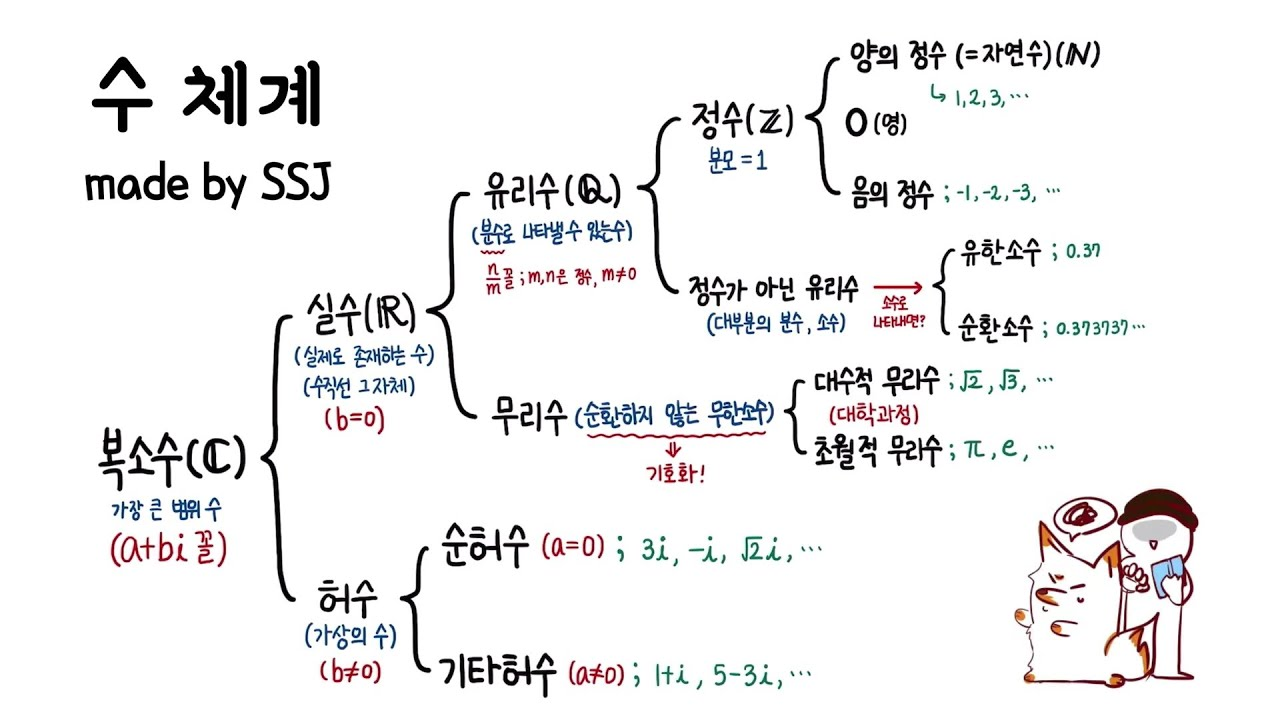 |
- 수의 체계에 포함되는 다양한 형태의 수를 이해하기 위해 수의 기수(Base)의 자릿수를 이해해야 한다.
기수(Base)
- 10진수, 2진수와 같이 수 표현의 근거를 알려주는 수
- 숫자의 끝에 아래 첨자로 표기한다.
- 일반적으로 10진수는 그 표기를 생략하기도 한다.
- 예) $143_{10}, 11001_{2}, …$
자릿수(Digit)
- 수를 구성하는 각 숫자의 위치
- 소수점을 기준으로 정한다.
| 10진 실수 $123.4567_{10}$ 의 각 숫자에 대한 자릿수 | ||||||||
| 10진 실수 | 1 | 2 | 3 | . | 4 | 5 | 6 | 7 |
| 자릿수 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | |
자연수(Natural Number : $\mathbb{N}$)
0보다 큰 양의 정수 $n, \;a, \;b ∈ \mathbb{N}$ 이고, $b > 1, \; 0 ≤ a_{i} < b$ ($a_{i}$ : 자연수 `n` 을 구성하는 `i` 번째 숫자, $i ≥ 0$)일 때,
$$n = a_{k}b^{k} + a_{k-1}b^{k-1} + … + a_{1}b^{1} + a_{0}b^{0} \quad \text(b : 기수, \; k : 자릿수)$$
예
- $589_{10} = 5 × 10^{2} + 8 × 10^{1} + 9 × 10^{0}$
정수(Integer : $\mathbb{Z}$)
양의 정수, 0, 음의 정수로 구성된 수
- 0 : 양의 정수나 음의 정수에 속하지 않는 수로, +나 -와 같은 부호가 붙지 않는다.
- 음의 정수 : 숫자 앞에 - 부호가 붙는 0보다 작은 수
- 양의 정수 : 숫자 앞에 + 부호가 붙거나 부호가 생략된 0보다 큰 수로, 자연수와 같은 범위의 수
예
- $|28|$ 을 갖는 모든 정수는 $+28$ 과 $-28$ 이다.
유리수(Rational Number: $\mathbb{Q}$)
$a, b ∈ \mathbb{Z}$ 이고, $a ≠ 0$ 일 때 $\frac{b}{a}$ 인 수
- 정수 집합은 유리수 집합에 포함된다.
- 양의 정수 `2` 는 유리수 `\frac{2}{1}(1, 2 ∈ \mathbb{Z}, 1 ≠ 0)` 로 표현할 수 있다.
- 유리수는 같은 값을 다르게 표현할 수 있다.
- 예) $\frac{6}{27} = \frac{2}{9}$
- $\frac{6}{27}, \frac{12}{24}, \frac{4}{8}$ 는 분자와 분모 사이에 1 이외의 공약수가 존재하여 약분이 가능하므로 하한항으로 표현되지 않은 유리수이다.
- 하한항(Lowest; 기약 분수) : 1 이외의 공약수가 존재하지 않는 분모와 분자
- 반면, 이 유리수들을 분자와 분모의 최대 공약수로 분자와 분모를 약분하면 하한항으로 구성된 유리수가 된다.
- 예) $\frac{1}{9}, \frac{1}{2}$
예
- $\frac{25}{70}$ 은 하한항으로 표현되지 않은 유리수이다. 분모 25와 분자 70의 공약수는 1과 5이기 때문이다. 최대 공약수인 5로 분모와 분자를 약분하여 하한항으로 표현하면 $\frac{5}{14}$ 와 같다.
- $\frac{7}{10}$ 은 하한항으로 표현된 유리수이다. 분모 10과 분자 70의 공약수는 1만 존재하기 때문이다.
무리수(Irrational Number : $\mathbb{I}$)
$a, b ∈ \mathbb{Z}$ 이고, $a ≠ 0$ 일 때 $\frac{b}{a}$ 로 표현할 수 없는 수
- 유리수 집합과 무리수 집합은 모두 실수 집합에 포함된다.
- 실수는 다음과 같이 소수점을 기준으로 정수부와 소수부로 구분하여 표현할 수 있다.
| 10진 실수 $123.4567_{10}$ | ||
| 123 | . | 4567 |
| 정수부 | 소수점 | 소수부 |
- 실수는 분수 형태($\frac{b}{a}, \quad a, b ∈ \mathbb{Z}, \quad a ≠ 0$)로 표현할 수 있으면 유리수, 그렇지 않으면 무리수로 구분한다.
- 유리수는 소수로 표현했을 때 ①소수부의 숫자가 유한하게 나열되거나 ②규칙성을 갖고 무한히 나열되는 형태로 나타나 분수로 표현 가능하다.
- 예1) $\frac{3}{4} = 0.75$ (소수부가 유한하다.)
- 예2) $\frac{1}{7} = 0.142857142857142857…$ (소수부에서 142857이 반복된다.)
- 예3) $\sqrt{9} = 3$ (정수)
- 무리수는 소수부의 숫자가 규칙성 없이 무한히 나열되어 분수로 표현할 수 없다.
- 예) $\sqrt{2} = 1.41213562373…$ (소수부의 숫자가 불규칙하게 나열되어 있다.)
예
- $\frac{5}{7} = 0.714285714285…$ 는 유리수이다.
- $\sqrt{11} = 3.3166247903…$ 으로 무리수이다.
실수(Real Number: $\mathbb{R}$)
$r ∈ \mathbb{R}, a_{i} ∈ \mathbb{Z}, b ∈ \mathbb{N}$ 이고 $b > 1, 0 ≤ a_{i} < b$ ($a_{i}$ : 실수 `r`을 구성하는 `i`번째 숫자, $i ∈ \mathbb{Z}$) 일 때,
$$r = a_{k}b^{k} + a_{k-1}b^{k-1} + … + a_{1}b^{1} + a_{0}b^{0} + a_{-1}b^{-1} + a_{-2}b^{-2} + … \quad \text(b : 기수, \; k : 자릿수)$$
- 유리수와 무리수를 모두 포함하는 수 체계
- 소수점을 기준으로 정수부와 실수부로 표현
예
- $34.8125_{10} = 3 × 10^{1} + 4 × 10^{0} + 8 × 10^{-1} + 1 × 10^{-2} + 2 × 10^{-3} + 5 × 10^{-4}$
허수 단위(Imaginary Unit)
$i^{2} = -1$ 을 만족하는 수 $i$
- 제곱하여 음수가 되는 실수는 없다.
- 그러나 물리학, 전자 공학 등에서는 제곱했을 때 0보다 작은 값이 되는 가상의 수가 필요한 경우가 있어, 이러한 허수 개념을 다양한 방정식에 적용하기도 한다.
복소수(Complex Number: $\mathbb{C}$)
$$c = a + bi \quad (a, b ∈ \mathbb{R}, c ∈ \mathbb{C})$$
$c$ : 복소수
$a$ : 실수부
$bi$ : 허수부
- 실수와 허수를 모두 포함하는 수 체계
- $b = 0$ 이면 실수, $b ≠ 0$ 이면 허수(Imaginary Number)
복소수의 사칙 연산 ($a, b, c, d ∈ \mathbb{R}$)
- 덧셈 : $(a + bi) + (c + di) = (a + c) + (b + d)i$
- 뺄셈 : $(a + bi) - (c + di) = (a - c) + (b - d)i$
- 곱셈 : $(a + bi)(c + di) = ac + adi + bci + bdi^{2} = (ac - bd) + (ad + bc)i$
- 나눗셈 : $\frac{a + bi}{c + di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac{ac - adi + bci + bd}{c^{2} -cdi + cdi + d^{2}} = \left( \frac{ac + bd}{c^{2} + d^{2}} \right) + \left( \frac{bc - ad}{c^{2} + d^{2}} \right)i \quad (\text{단}, c+di ≠ 0)$
예
- $3 + 6i + 12i = 3 + 18i$
- $3 + 6i - 12i = 3 - 6i$
- $(3 + 6i) × 12i = -72 + 36i$
- $\frac{3 + 6i}{12i} = \frac{72}{144} + \frac{-36}{144}i = \frac{2-i}{4}$
- 분모와 분자에 $-12i$ 를 곱해준다.
728x90
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 조건 명제 (0) | 2022.10.02 |
|---|---|
| [이산 수학] 논리 연산자 (0) | 2022.10.02 |
| [이산 수학] 명제 (0) | 2022.10.02 |
| [이산 수학] 컴퓨터에서의 수의 표현과 연산 (0) | 2022.09.27 |
| [이산 수학] 진법별 사칙연산 (0) | 2022.09.26 |
| [이산 수학] 진법 간 변환 (0) | 2022.09.20 |
| [이산 수학] 진법별 표현 (0) | 2022.09.20 |
| [이산 수학] 수의 연산 (0) | 2022.09.19 |
