연속 확률 변수
- 이산 확률 변수는 확률 변수 `X` 가 취할 수 있는 값이 하나하나 떨어져 있으며, 그 값이 유한개이거나 셀 수 있는 값이다.
- 그러나 하루 동안 최저 온도 -10℃ 에서 최고 온도 5℃까지 수온주의 높이를 확률 변수 `X` 라 하면, `X` 가 취할 수 있는 값은 구간 [-10, 5] 안의 모든 실수로 나타난다.
- 이와 같이 확률 변수 `X` 의 상태 공간이 구간으로 나타나는 경우에도 확률 함수와 분포 함수 및 확률을 계산할 수 있다.
연속 확률 변수의 의미
- 온도계 수온주의 높이, 택시 정류장에서 기다리는 시간, 새로 교체한 전구의 수명 등과 같이 확률 변수가 취하는 값이 어떤 구간인 경우를 생각할 수 있다.
- 이 때, 온도계 수온주의 높이는 유한 구간이고, 전구의 수명은 무한 구간이다.
연속 확률 변수(Continuous Random Variable)
확률 변수 `X` 의 상태 공간이 유한 구간 $[a, b], \; (a, b)$ 또는 무한 구간 $[0, \infty), \; (-\infty, \infty)$ 인 확률 변수
예제 : 다음을 나타내는 확률 변수가 연속 확률 변수인지 아닌지 판단하라.
(a) 20세 이상인 성인의 키
(b) 하루 동안 접수된 신청서 건수
(a)
키는 구간으로 나타내므로 연속 확률 변수이다.
(b)
신청서 건수는 셀 수 있으므로 이산 확률 변수이다.
확률 밀도 함수(Probability Density Function)
다음 조건을 만족하는 음이 아닌 함수 `f(x)` 를 연속 확률 변수 `X` 의 확률 밀도 함수(Probability Density Function)라 한다.
$$\int_{-\infty}^{\infty} f(x)dx = 1$$
- 성인 남자의 키와 같이 구간으로 나타내는 자료에 대한 상대 도수 히스토그램을 그려보자.
- 이 때, 조사한 성인 남자의 수를 늘리면, 히스토그램은 아래와 같이 계급 간격은 줄어들고 계급의 수는 늘어난다.
- 그리고 직사각형의 넓이는 각 계급의 상대 도수에 의한 확률을 나타낸다.
- 따라서 모든 직사각형의 넓이의 합은 전체 확률의 합이므로 1이다.
- 특히, 조사한 남자들 중에서 임의로 선정한 사람의 키가 168cm 이상 170cm 이하일 확률을 구하면, 이 확률은 색칠한 부분의 넓이다.
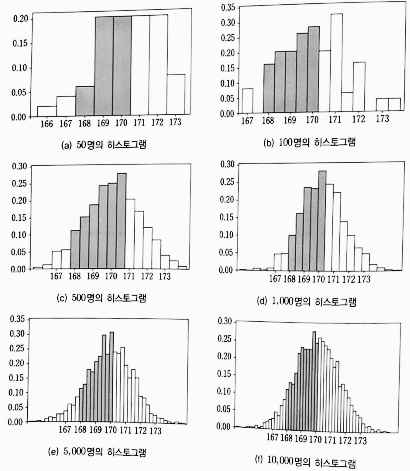
- 이와 같이 어떤 구간으로 주어지는 측정값의 개수를 늘릴수록, 계급 간격은 조밀해지고 상대 도수 히스토그램은 아래와 같은 어떤 형태의 곡선에 가까워진다.
- 그리고 구하고자 하는 확률은 이 곡선의 색칠한 부분의 넓이와 같아진다.
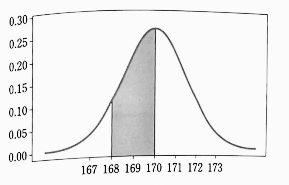
- 위의 곡선을 나타내는 함수를 `f(x)` 라 하면, 이 함수의 그래프는 항상 `x` 축 위에 있다.
- 또한 모든 상대 도수의 합이 1이므로, 함수 `f(x)` 와 `x` 축으로 둘러싸인 부분의 넓이는 1이다.
- 이 때, 함수 `f(x)` 를 다음과 같이 연속 확률 변수 `X` 의 확률 밀도 함수라고 한다.
연속 확률 변수에 대한 확률 계산
- 임의의 실수 $a, b \; (a < b)$ 에 대해, 확률 $P(a \le X \le b)$ 은 $x = a$ 와 $x = b$ 그리고 `x` 축과 `f(x)` 로 둘러싸인 부분의 넓이이고, 이를 나타내면 다음과 같다.
$$P(a \le X \le b) = \int_{a}^{b}f(x)dx$$
- 특히 연속 확률 변수 `X` 가 특정한 값 `a` 를 취할 확률은 `a` 가 상태 공간 안에 있더라도 다음과 같다.
$$P(X = a) = 0$$
- 따라서 연속 확률 변수 `X` 가 취하는 구간의 경계값은 확률 계산에 아무런 영향을 미치지 않으며, 연속 확률 변수 `X` 에 대해 다음 성질이 성립한다.
① $\displaystyle P(X \ge a) = P(X > a) = \int_{a}^{\infty} f(x)dx$
② $\displaystyle P(X \le a) = P(X < a) = \int_{-\infty}^{a} f(x)dx$
③ $\displaystyle P(a \le X \le b) = P(a < X \le b) = P(a \le X < b) = P(a < X < b) = \int_{a}^{b} f(x)dx$
④ $\displaystyle P(a \le X \le b) = P(X \le b) - P(X \le a)$
예제 : 어떤 상수 `k` 에 대해 함수 `f(x)` 가 연속 확률 변수 `X` 의 확률 밀도 함수라 할 때, 다음을 구하라.
| $$f(x) = \begin{cases} kx, & 0 \le x \le 4 \\ 0, & \text{otherwise} \end{cases}$$ |
(a) 상수 `k`
(b) $P(2 < X \le 3)$
(a)
`f(x)` 가 확률 밀도 함수이므로 다음이 성립한다.
$\displaystyle \int_{-\infty}^{\infty} f(x)dx = \int_{0}^{4} kxdx = \left [ \frac{k}{2}x^{2} \right]^{4}_{0} = 8k = 1$
따라서 구하고자 하는 상수는 $k = \frac{1}{8}$ 이다.
(b)
$\displaystyle P(2 < X \le 3) = \frac{1}{8} \int_{2}^{3} xdx = \left [\frac{1}{16}x^{2} \right]^{3}_{2} = \frac{9 - 4}{16} = \frac{5}{16}$
연속 확률 변수의 분포 함수
- 이산 확률 변수 `X` 에 대해 분포 함수 `F(x)` 를 정의한 것과 마찬가지로, 연속 확률 변수의 분포 함수를 정의할 수 있다.
연속 확률 변수 `X` 에 대한 분포 함수를 다음과 같이 정의한다.
$$F(x) = P(X \le x) = \int_{-\infty}^{x} f(u)du$$
- 연속 확률 변수 `X` 에 대한 분포 함수 `F(x)` 는 무한 구간 $(-\infty, x]$ 에서 확률 밀도 함수 `f(x)` 를 적분한 결과이다.
- 연속 확률 변수 `X` 의 분포 함수는 다음과 같이 임의의 실수 `x` 보다 작거나 같은 영역에서 함수 `f(x)` 로 둘러싸인 부분의 넓이이다.
- 그리고 분포 함수 `F(x)` 는 모든 점에서 연속이고, 보편적으로 `S` 모양을 이룬다.
| 분포 함수의 의미 | 분포 함수 |
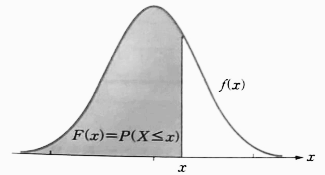 |
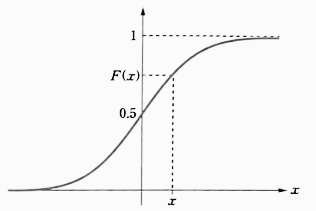 |
분포 함수와 확률
- 임의의 두 실수 $a, b \; (a < b)$ 에 대해 분포 함수를 이용하여 다음과 같이 확률을 구할 수 있다.
① $P(X \ge a) = 1 - P(X < a) = 1 - F(a)$
② $P(a \le X \le b) = P(a < X \le b) = P(a \le X < b) = P(a < X < b) = F(b) - F(a)$
확률 밀도 함수 `f(x)` 와 분포 함수 `F(x)` 사이의 관계
- 연속 확률 변수 `X` 의 확률 밀도 함수 `f(x)` 와 분포 함수 `F(x)` 사이에 다음 관계가 성립한다.
$$f(x) = \frac{d}{dx} F(x) \Leftrightarrow F'(x) = f(x) \\ f(x) = P(X \le x) = \int_{-\infty}^{x} f(t)dt $$
예제 : 연속 확률 변수 `X` 의 분포 함수가 $F(x) = 1 -e^{-2x}, \; x > 0$ 일 때, 다음을 구하라.
(a) 확률 밀도 함수 `f(x)`
(b) $P(X > 2)$
(c) $P(1 < X \le 2)$
(a)
`X` 의 확률 밀도 함수 `f(x)` 는 다음과 같이 분포 함수 `F(x)` 를 미분하여 얻는다.
$\displaystyle f(x) = \frac{d}{dx}(1 - e^{-2x}) = 2e^{-2x}, \; x > 0$
(b)
$P(X > 2) = 1 - P(x \le 2) = 1 - F(2) = 1 - (1 - e^{-4}) = e^{-4}$
(c)
$P(1 < X \le 2) = F(2) - F(1) = (1 - e^{-4}) - (1 - e^{-2}) = e^{-2} - e^{-4}$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
|---|---|
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 이산 확률 변수 (0) | 2022.11.07 |
| [확률과 통계] 베이즈 정리 (0) | 2022.10.31 |
| [확률과 통계] 조건부 확률 (0) | 2022.10.31 |
| [확률과 통계] 확률 (0) | 2022.10.31 |


