모집단과 표본
- 기술 통계학에서 통계 목적에 부합하는 모든 자료 집단을 모집단이라고 한다.
- 예를 들어, 우리나라는 5년 주기로 인구 주택 총조사를 실시한다. 이 때 모든 가구를 대상으로 가족 구성원의 연령을 비롯하여 가구 형태 등을 조사한다.
- 이와 같이 통계 목적에 부합하는 모든 자료들의 집단을 모집단이라고 하며, 이 모집단 전체를 대상으로 조사하는 것을 전수 조사(Complete Survey)라 한다.
- 한편, 선거철이 되면 방송이나 신문에서 "신뢰도 95%와 표본 오차 5%에서 A 후보의 지지율이 30% 이다." 라는 내용을 자주 접한다.
- 이 경우는 모든 유권자(모집단) 중에서 일부(표본)만 대상으로 조사한 결과를 나타낸다.
- 이와 같이 표본을 대상으로 조사하는 것을 표본 조사(Sampling Survey)라 한다.
모집단 분포와 표본 분포
모집단 분포(Population Distribution)와 모수(Parameter)
- 모집단 분포(Population Distribution) : 어떤 통계적인 목적 아래 수집한 모든 자료가 갖는 확률 분포 (모집단이 이루는 확률 분포)
- 모수(Parameter) : 모집단의 특성을 나타내는 수치
- 모집단의 평균을 모평균(Population Mean), 모집단의 분산과 표준 편차를 각각 모분산(Population Variance)과 모표준 편차(Population Standard Deviation)라고 한다.
- 지지율과 같이 모집단에서 어떤 특정한 성질을 갖는 자료의 비율을 모비율(Population Proportion)이라 한다.
- 일반적으로 모평균은 `μ`, 모분산은 $σ^{2}$, 모비율은 `p` 로 나타내며, 크기 `N` 인 모집단에 대해 다음과 같이 정의한다.
- 모평균 : $\displaystyle μ = \frac{1}{N} \sum_{i=1}^{N}X_{i}$
- 모분산 : $\displaystyle σ^{2} = \frac{1}{N} \sum_{i=1}^{N} (X_{i} - μ)^{2}$
- 모표준 편차 : $\displaystyle σ = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (X_{i} - μ)^{2}}$
- 모비율 : $\displaystyle p = \frac{X}{N}$, `X` 는 특정한 성질을 갖는 자료의 수
- 한편, 전수 조사를 실시하기 곤란하거나 불가능한 경우에 모집단 분포는 알려지지 않는다.
- 따라서 모집단에 대한 분포를 비롯하여 모수를 알기 위해 표본 조사를 실시하여 얻은 결과를 이용하여 추측한다.
- 이 때, 잘못된 표본을 선정하여 조사한다면, 모집단에 대한 왜곡된 정보를 얻게 된다.
- 따라서 이러한 오류를 방지하기 위해 모집단을 구성하는 각 원소가 선정될 확률이 동등하게 추출하며, 이러한 추출 방법을 임의 추출(Random Sampling)이라 한다.
- 임의 추출에 의해 얻은 표본에 대한 평균은 표본 평균(Sample Mean), 표본의 분산과 표준 편차를 각각 표본 분산(Sample Variance)과 표본 표준 편차(Sample Standard Deviation), 그리고 표본의 비율을 표본 비율(Sample Proportion)이라 한다.
- 이와 같이 표본의 특성을 나타내는 통계적인 양을 통계량(Statistics)이라 하며, 통계량은 표본의 선정에 따라 다른 값을 갖게 된다.
- 따라서 통계량은 확률 변수이며, 통계량의 확률 분포를 표본 분포(Sampling Distribution)라 한다.
표본 분포와 통계량
- 통계량(Statistics) : 표본의 특성을 나타내는 통계적인 양
- 표본 분포(Sampling Distribution) : 표본으로부터 얻은 통계량의 확률 분포
- 일반적으로 표본 평균은 $\overline{X}$, 표본 분산은 $S^{2}$, 표본 비율은 $\hat{p}$ 로 나타내며, 다음과 같이 정의한다.
- 표본 평균 : $\displaystyle \overline{X} = \frac{1}{n} \sum_{i=1}^{n}X_{i}$
- 표본 분산 : $\displaystyle S^{2} = \frac{1}{n - 1} \sum_{i=1}^{n} (X_{i} - \overline{x})^{2}$
- 표본 표준 편차 : $\displaystyle S = \sqrt{\frac{1}{n - 1} \sum_{i=1}^{n} (X_{i} - \overline{x})^{2}}$
- 표본 비율 : $\displaystyle \hat{p} = \frac{X}{n}$, `X` 는 특정한 성질을 갖는 자료의 수
예제 : 소수점 이하 셋짜 자리에서 반올림하여 다음을 구하여라.

(a) 모평균
(b) 모분산
(c) 모표준 편차
(a)
$\sum x_{i} = 402.88$ 이므로, 모평균은 다음과 같다.
| $$μ = \frac{1}{33} \sum_{i=1}^{33} x_{i} = \frac{402.88}{33} = 12.21(km)$$ |
(b)
$\sum (x_{i} - μ)^{2} = 1232.53$ 이므로 모분산은 다음과 같다.
| $$σ^{2} = \frac{1}{33} \sum_{i=1}^{33} (x_{i} - μ)^{2} = \frac{1232.53}{33} = 37.35$$ |
(c)
모표준 편차는 모분산의 양의 제곱근이므로 $σ = \sqrt{37.35} = 6.11(km)$ 이다.
※ 단위는 평균과 표준 편차를 구할 때 붙이고, 분산을 구할 때는 붙이지 않는다.
표본 평균의 분포
- 표본의 크기에 따라 표본 평균의 분포가 어떻게 변하는지 살펴보고, 모평균과의 관계를 알아보자.
- 1, 2, 3, 4의 숫자가 적힌 카드가 들어있는 주머니에서 카드를 꺼낸다고 할 때, 추출된 카드의 숫자를 확률 변수 `X` 라 하면, 모집단 분포는 다음과 같다.
- 확률 변수 `X` 의 모평균은 `μ = 2.5` 이고, 모분산은 $σ^{2} = \frac{5}{4}$ 이다.
| `X` | 1 | 2 | 3 | 4 |
| $P(X = x)$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ |
- 이제 복원 추출로 주머니에서 카드를 2장 꺼내 첫 번째 카드의 수를 $X_{1}$, 두 번째 카드의 수를 $X_{2}$ 라 하자.
- 그러면 나올 수 있는 모든 경우 $(x_{1}, x_{2})$ 는 다음과 같다.
| $$\begin{Bmatrix} (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4) \\ (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)\end{Bmatrix}$$ |
- 그러므로 표본 평균 $\displaystyle \overline{X} = \frac{X_{1} + X_{2}}{2}$ 가 취할 수 있는 값은 $1, 1.5, 2, 2.5, 3, 3.5, 4$ 뿐이고, $\overline{X}$ 의 확률 분포는 다음과 같다.
| $\overline{X}$ | $1$ | `3/2` | $2$ | `5/2` | `3` | `7/2` | 4 |
| $P(\overline{X} = \overline{x})$ | `1/16` | `2/16` | `3/16` | `4/16` | `3/16` | `2/16` | `1/16` |
- 따라서 크기가 2인 표본 평균 $\overline{X}$ 의 평균과 분산은 각각 다음과 같다.
| $$E(\overline{X}) = \sum \overline{x} P(\overline{X} = \overline{x}) = \frac{5}{2}, \quad \text{Var}(\overline{X}) = \sum \overline{x}^{2} P(\overline{X} = \overline{x}) - \left ( \frac{5}{2} \right )^{2} = \frac{5}{8}$$ |
- 그러므로 크기 2인 표본 평균 $\overline{X}$ 의 평균을 $μ_{\overline{X}}$ 와 분산 $σ_{\overline{X}}^{2}$ 그리고 모평균 $μ$ 와 모분산 $σ^{2}$ 사이에는 다음 관계가 성립한다.
| $$μ_{\overline{X}} = μ = \frac{5}{2}, \quad σ_{\overline{X}}^{2} = \frac{σ^{2}}{2} = \frac{5}{8}$$ |
- 한편, 이 모집단에서 크기가 3인 표본 $\{X_{1}, X_{2}, X_{3} \}$ 을 추출하여 표본 평균 $\displaystyle \overline{X} = \frac{X_{1} + X_{2} + X_{3}}{3}$ 의 확률 분포를 구하면 다음과 같다.
| $\overline{X}$ | `1` | `4/3` | `5/3` | `2` | `7/3` | `8/3` | `3` | `10/3` | `11/3` |
| $P(\overline{X} = \overline{x})$ | `1/64` | `3/64` | `6/64` | `10/64` | `12/64` | `12/64` | `10/64` | `6/64` | `3/64` |
- 이 때, 크기 3인 표본 평균 $\overline{X}$ 의 평균과 분산은 각각 다음과 같다.
| $$E(\overline{X}) = \sum \overline{x} P(\overline{X} = \overline{x}) = \frac{5}{2}, \quad \text{Var}(\overline{X}) = \sum \overline{x}^{2} P(\overline{X} = \overline{x}) - \left ( \frac{5}{2} \right )^{2} = \frac{5}{12}$$ |
- 따라서 $\overline{X}$ 의 평균과 분산, 그리고 모평균과 모분산 사이에는 다음 관계가 성립한다.
| $$μ_{\overline{X}} = μ = \frac{5}{2}, \quad σ_{\overline{X}}^{2} = \frac{σ^{2}}{3} = \frac{5}{12}$$ |
- 이와 같은 방법으로 크기가 `n` 인 표본을 선정하여 표본 평균을 $\overline{X}$ 라 하면, 표본 평균 $\overline{X}$ 의 평균 $μ_{\overline{X}}$ 는 모평균 `μ` 와 동일하고, 표본 평균 $\overline{X}$ 의 분산 $σ_{\overline{X}}^{2}$ 는 모분산 $σ^{2}$ 을 표본의 크기 `n` 으로 나눈 것과 같음을 알 수 있다.
- 일반적으로 모평균 `μ` 와 모분산 $σ^{2}$ 인 모집단에서 크기 `n` 인 표본을 선정할 때, 표본 평균 $\overline{X}$ 의 평균과 분산에 대해 다음이 성립한다.
$$μ_{\overline{X}} = μ, \quad σ_{\overline{X}}^{2} = \frac{σ^{2}}{n}$$
- 또한 모집단 분포가 이산 확률 분포로 균등하게 나타나더라도 표본 평균의 표본 분포는 아래와 같이 `n` 이 커질수록 종 모양으로 변하는 것을 알 수 있다.
- 즉, `n` 이 커질수록 표본 평균 $\overline{X}$ 의 분포는 정규 분포에 근사한다.
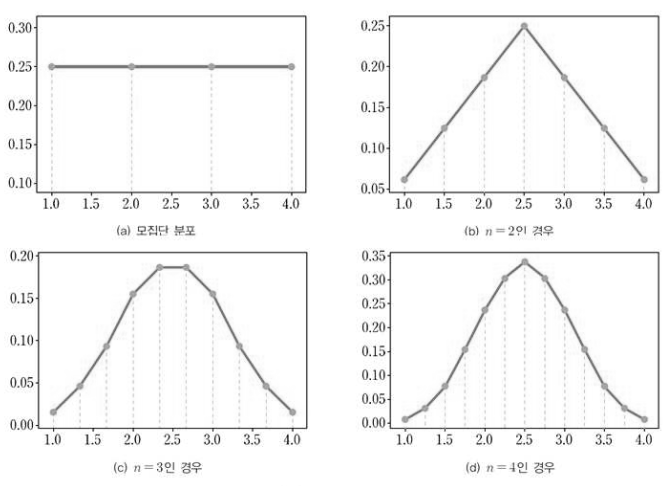
표본 평균의 특성
- 모평균 `μ` 와 모분산 $σ^{2}$ 인 모집단에서 크기 `n` 인 표본을 선정할 때, 표본 평균 $\overline{X}$ 의 표본 분포에 대해 다음이 성립한다.
(1) 표본 평균의 평균은 $\displaystyle μ_{\overline{X}} = μ$ 이고, 분산은 $\displaystyle σ_{\overline{X}}^{2} = \frac{σ^{2}}{n}$ 이다.
(2) 모집단이 정규 분포 $\displaystyle N(μ, \; σ^{2})$ 이면, `n` 의 크기에 관계 없이 $\displaystyle \overline{X} \sim N(μ, \; \frac{σ^{2}}{n})$ 이다.
(3) 모집단의 분포가 정규 분포가 아닌 경우에도 충분히 큰 `n` 에 대해 근사적으로 $\displaystyle \overline{X} \approx N(μ, \; \frac{σ^{2}}{n})$ 이다.
예제 : 모집단의 확률 분포가 다음과 같다.
이 모집단에서 크기가 2인 표본을 복원 추출할 때, 표본 평균 $\overline{X}$ 에 대해 다음을 구하라.
`X` `-1` `0` `1` $P(X=x)$ `1/3` `1/2` `1/6`
(a) $\overline{X}$ 의 분포
(b) $\overline{X}$ 의 평균
(c) $\overline{X}$ 의 분산
(a)
크기가 2인 표본을 $\{X_{1}, X_{2} \}$ 이라 하면, 복원 추출이므로 다음이 성립한다.
| $$P(X_{1} = x_{1}, \; X_{2} = x_{2}) = P(X_{1} = x_{1})P(X_{2} = x_{2}), \; x_{1}, x_{2} = -1, 0, 1$$ |
따라서 다음 확률표를 얻는다.
| $X_{2}$ \ $X_{1}$ | `-1` | `0` | `1` |
| `-1` | `1/9` | `1/6` | `1/18` |
| `0` | `1/6` | `1/4` | `1/12` |
| `1` | `1/18` | `1/12` | `1/36` |
아 때, 표본 평균 $\displaystyle \overline{X} = \frac{X_{1} + X_{2}}{2}$ 가 취할 수 있는 값은 `-1, -0.5, 0, 0.5, 1` 뿐이고, $\overline{X}$ 의 확률 분포는 다음과 같다.
| $\overline{X}$ | `-1` | `-0.5` | `0` | `0.5` | `1` |
| $P(\overline{X} = \overline{x})$ | `4/36` | `12/36` | `13/36` | `6/36` | `1/36` |
(b)
모평균이 $μ = - \frac{1}{6}$ 이므로, $\overline{X}$ 의 평균은 $μ_{\overline{X}} = - \frac{1}{6}$ 이다.
(c)
모분산이 $σ^{2} = \frac{17}{36}$ 이므로, $\overline{X}$ 의 분산은 $σ_{\overline{X}}^{2} = \frac{17/36}{2} = \frac{17}{72}$ 이다.
표본 비율의 분포
- 모비율이 `p` 인 모집단에서 크기 `n` 인 표본을 임의로 선정하여 표본을 $\{X_{1}, X_{2}, \cdots, X_{n} \}$ 이라 하자.
- 그러면 $X_{i}, \; i = 1, 2, \cdots, n$ 은 0 또는 1 을 취하는 확률 변수이고, $X = X_{1} + X_{2} + \cdots + X_{n}$ 은 표본에서 성공한 횟수를 나타낸다.
- 따라서 `n` 개로 구성된 표본 중에서 특정 사건이 나타나는 비율인 표본 비율은 $\displaystyle \hat{p} = \frac{X}{n}$ 이다.
- 독립인 베르누이 확률 변수들의 합 `X` 에 대해 $X \sim B(n, \; p)$ 이므로, 확률 변수 `X` 의 평균과 분산은 각각 $μ = np$ 와 $σ^{2} = npq$ 이고, 따라서 표본 비율 $\hat{p}$ 의 평균과 분산은 다음과 같다.
$$μ_{\hat{p}} = E \left (\frac{X}{n} \right ) = \frac{1}{n}E(X) = \frac{1}{n}(np) = p \\ σ_{\hat{p}}^{2} = \text{Var} \left (\frac{X}{n} \right ) = \frac{1}{n^{2}} \text{Var}(X) = \frac{1}{n^{2}}(npq) = \frac{pq}{n}$$
- 이 때, `n` 이 충분히 크면 이항 분포의 정규 근사에 의해 표본 비율 $\hat{p}$ 는 평균 $μ_{\hat{p}}$ 와 분산 $σ_{\hat{p}}^{2}$ 을 갖는 정규 분포에 근사한다.
- 즉, 표본 비율의 표본 분포는 다음과 같다.
$$\hat{p} \approx N \left( p, \frac{pq}{n} \right)$$
예제 : 모비율이 `p = 0.45` 인 모집단에서 크기 100인 표본을 추출했다. 표본 비율 $\hat{p}$ 에 대해 다음을 구하라.
(a) $\hat{p}$ 의 분포
(b) $P(\hat{p} \le 0.35)$
(c) $P(0.41 \le \hat{p} \le 0.51)$
(a)
$p = 0.45, \; n = 100$ 이므로 $\displaystyle μ_{\hat{p}} = 0.45, \; σ_{\hat{p}}^{2} = \frac{0.45 \times 0.55}{100} ≒ 0.05^{2}, \; \hat{p} \approx N(0.45, 0.05^{2})$ 이다.
(b)
$\displaystyle \eqalign{ P(\hat{p} \le 0.35) &= P \left ( \frac{\hat{p} - 0.45}{0.05} \le \frac{0.35 - 0.45}{0.05} \right ) \\ &= P(Z \le -2) = 1 - P(Z \le 2) = 1 - 0.9772 = 0.0228}$
(c)
$\displaystyle \eqalign{ P(0.41 \le \hat{p} \le 0.51) & = P \left ( \frac{0.41 - 0.45}{0.05} \le \frac{\hat{p} - 0.45}{0.05} \le \frac{0.51 - 0.45}{0.05} \right ) \\ & = P(-0.8 \le Z \le 1.2) \\ & = P(Z \le 1.2) - P(Z \le -0.8) \\ & = P(Z \le 1.2) - [1 - P(Z \le 0.8)] \\ & = 0.8849 - (1 - 0.7881) = 0.6730 }$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모평균의 검정(σ² : 기지) (0) | 2022.11.30 |
|---|---|
| [확률과 통계] 통계적 가설 검정 (0) | 2022.11.28 |
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 이산 확률 분포 (0) | 2022.11.14 |
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |


