이산 확률 분포
- 일반적으로 통계 모형에서 사용되는 확률 분포는 확률 함수에 의해 결정되는데, 이 때 확률 함수를 살펴보면 특정한 숫자에 의해 동일한 유형으로 나타난다.
- 특히 이산 확률 변수의 확률 분포를 이산 확률 분포라 한다.
베르누이 분포(Bernoulli Distribution)
- 동전 던지기의 앞면과 뒷면, 생산한 제품의 양호와 불량, 그리고 설문조사의 YES와 NO 등과 같이 실험 결과가 2가지인 확률 실험을 베르누이 실험(Bernoulli Experiment)이라 한다.
- 이 실험에서 관심의 대상이 되는 실험 결과를 성공, 그렇지 않은 결과를 실패라 하고, 성공의 확률 `p` 를 성공률(Rate of Success)이라 한다.
예
- 주사위를 던져서 1의 눈이 나오는 게임을 한다면, 관심의 대상은 1의 눈이고, 성공률은 $\displaystyle \frac{1}{6}$ 이다.
- 주사위를 던져서 1의 눈이 나오면(성공) 확률 변수 `X = 1`, 다른 눈이 나오면(실패) `X = 0` 이라 하자.
- 그러면 확률 변수 `X` 의 확률 질량 함수는 다음과 같다.
| $$f(x) = \begin{cases} \frac{5}{6}, & x = 0 \\ \frac{1}{6}, & x = 1 \\ 0, & otherwise \end{cases}$$ |
- 이처럼 성공률이 `p` 인 베르누이 실험에서 성공이면 `X = 1`, 실패이면 `X = 0` 이라 할 때, 확률 변수 `X` 의 확률 분포를 모수 `p` 인 베르누이 분포(Bernoulli Distribution)라 한다.
- 이 때, `X` 의 확률 질량 함수를 나타내면 다음과 같다.
$$f(x) = \begin{cases} 1 - p, & x = 0 \\ p, & x = 1 \\ 0, & otherwise \end{cases}$$
- 특히 성공률 `p` 인 베르누이 실험을 독립적으로 반복하여 실행하는 과정을 베르누이 실행(Bernoulli Trial)이라 한다.
- 확률 변수 `X` 가 모수 `p` 인 베르누이 분포를 따른다면, `X` 와 $X^{2}$ 의 평균은 각각 다음과 같다.
$$E(X) = (1 - p) \times 0 + p \times 1 = p \\ E(X^{2}) = (1 - p) \times 0^{2} + p \times 1^{2} = p$$
- 따라서 `X` 의 분산은 $σ^{2} = E(X^{2}) - \{E(X)\}^{2} = p - p^{2} = p(1 - p)$ 이다.
① `X` 의 평균 : $μ = p$
② `X` 의 분산 : $σ^{2} = p(1 - p)$
예제 : 주사위를 던져서 5 또는 6의 눈이 나오면 `X = 1`, 다른 눈이 나오면 `X = 0` 이라 할 때, 확률 변수 `X` 의 확률 질량 함수 `f(x)` 와 `X` 의 평균과 분산을 구하라.
주사위를 던져서 5 또는 6의 눈이 나올 확률은 $p = \frac{1}{3}$ 이고, 다른 눈이 나올 확률은 $1 - p = \frac{2}{3}$ 이므로, $P(X = 0) = \frac{2}{3}, \; P(X=1)=\frac{1}{3}$ 이다. 따라서 `X` 의 확률 질량 함수는 다음과 같다.
$\displaystyle f(x) = \begin{cases} \frac{2}{3}, & x = 0 \\ \frac{1}{3}, & x = 1 \\ 0, & otherwise \end{cases}$
그리고 `X` 의 평균은 $μ = \frac{1}{3}$, 분산은 $σ^{2} = \frac{1}{3} \times \frac{2}{3} = \frac{2}{9}$ 이다.
이항 분포(Binomial Distribution)
매회 성공률이 `p` 인 베르누이 실험을 독립적으로 `n` 번 반복할 때, 성공한 횟수(`X`)의 확률 분포를 모수 `n` 과 `p` 인 이항 분포(Binomial Distribution)라 하고, $X \sim B(n, p)$ 로 나타낸다.
예
- 주사위를 네 번 던지는 게임에서 1의 눈이 나온 횟수를 생각해보자.
- 매 시행에서 1의 눈이 나오면 `S`, 다른 눈이 나오면 `F` 라 하면 표본 공간은 다음과 같다.
| $$\begin{Bmatrix} SSSS, SSSF, SSFS, SFSS, SSFF, SFSF, SFFFS, SFFF \\ FSSS, FSSF, FSFS, FFSS, FSFF, FFSF, FFFS, FFFF \end{Bmatrix}$$ |
- 주사위를 던지는 게임은 독립 시행이므로 시행에서 성공률은 $P(S) = \frac{1}{6}$, 실패율은 $P(F) = \frac{5}{6}$ 이다.
- 이 때, 꼭 한 번 성공하는 사건은 $A = \{SFFF, FSFF, FFSF, FFFS \}$ 이고, 각 표본점에 대응하는 확률은 $\displaystyle \frac{1}{6} \left( \frac{5}{6} \right)^{3}$ 이다.
- 그러므로 주사위를 네 번 던지는 게임에서 확률 변수 `X` 를 성공 횟수라 하면, `X = 1` 인 확률은 다음과 같다.
| $$P(X = 1) = 4 \times \frac{1}{6} \left( \frac{5}{6} \right)^{3} = {}_{4}C_{1}\frac{1}{6} \left( \frac{5}{6} \right)^{3}$$ |
- 그리고 $P(X = 1)$ 은 다음과 같은 구조를 갖는다.
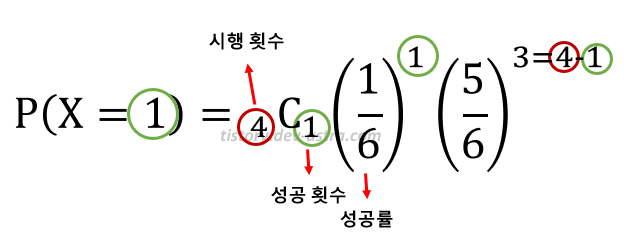
- 따라서 4번의 시행 중에서 성공한 횟수를 나타내는 확률 변수 `X` 가 취할 수 있는 값은 0, 1, 2, 3, 4 이고, 다음과 같은 확률의 구조를 얻는다.
| $$P(X = x) = {}_{4}C_{x} \left( \frac{1}{6} \right)^{x} \left( \frac{5}{6} \right)^{4-x}, \quad x = 0, 1, 2, 3, 4$$ |
매회 성공률이 `p` 인 베르누이 시행을 `n` 번 독립적으로 반복하여 성공한 횟수에 대한 확률
- 일반적으로 매회 성공률이 `p` 인 베르누이 시행을 `n` 번 독립적으로 반복하여 성공한 횟수를 확률 변수 `X` 라 하자.
- 이 때, `n` 번의 시행 중에서 `x` 번 성공하는 경우의 수는 $\displaystyle {}_{n}C_{x} = \frac{n!}{x!(n-x)!}$ 이고, 독립 시행이므로 `x` 번 성공하는 경우의 각 경우의 확률은 $p^{x}(1-p)^{n-x}$ 이다.
- 따라서 매회 성공률이 `p` 인 베르누이 시행을 `n` 번 독립적으로 반복하여 성공한 횟수에 대한 확률은 다음과 같다.
$$P(X = x) = {}_{n}C_{x} p^{x} (1 - p)^{n-x}, \quad x = 0, 1, 2, \cdots, n$$
- 그리고 모수 `n` 과 `p` 인 이항 분포의 확률 질량 함수는 다음과 같다.
$$f(x) = \begin{cases} {}_{n}C_{x}p^{x}q^{n-x} &, x=0, 1, 2, \cdots, n, \; q = 1 - p \\ 0 &, otherwise \end{cases}$$
이항 분포($B(n, p)$)의 그래프
- 이항 분포 $B(n, p)$ 의 그래프는 다음과 같다.
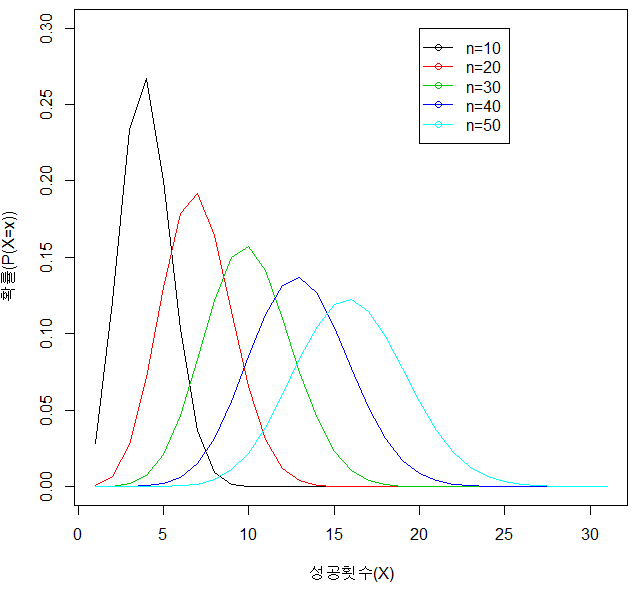
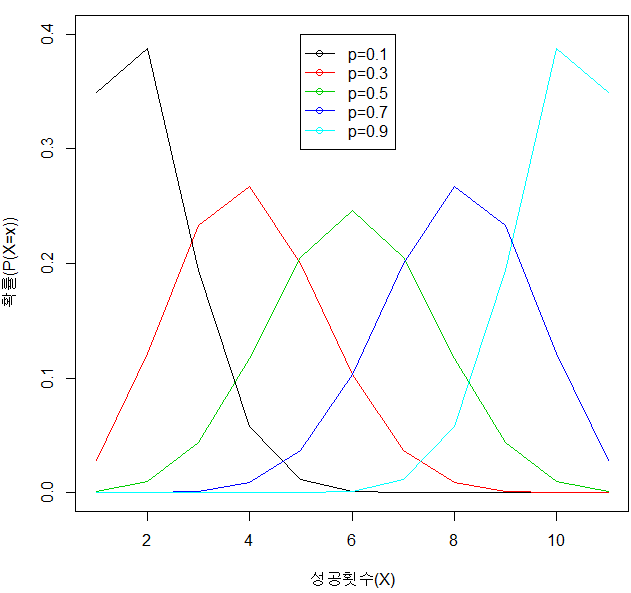
| `n` 에 따른 이항 분포의 그래프 | `p` 에 따른 이항 분포의 그래프 |
 |
 |
- `p` 가 일정하고 `n` 이 커지면 이항 분포는 종 모양의 좌우 대칭형에 가까워진다.
- $\color{red}{ p < 0.5}$ 이면 이항 분포는 왼쪽으로 치우치고, 오른쪽으로 긴 꼬리 모양을 가지는 양의 비대칭인 분포를 이룬다.
- $\color{red}{ p > 0.5}$ 이면 이항 분포는 오른쪽으로 치우치고 왼쪽으로 긴 꼬리 모양을 가지는 음의 비대칭인 분포를 이룬다.
- $\color{red}{ p = 0.5}$ 이면 `n` 에 관계 없이 $μ = \frac{n}{2}$ 을 중심으로 좌우 대칭이다.
- 이 경우를 대칭 이항 분포(Symmetric Binomial Distribution)라 한다.
이항 분포에 따르는 확률 변수 `X` 의 평균과 분산
- 매회 성공률이 `p` 인 베르누이 시행을 `n` 번 독립적으로 반복하여 `i` 번째 시행에서 성공이면 $X_{i} = 1$ 실패이면 $X_{i} = 0$ 이라 하자.
- 그러면 $E(X_{i}) = p, \; \text{Var}(X_{i}) = p(1 - p), \; i = 1, 2, \cdots, n$ 이다.
- 이 때, 각 확률 변수 $X_{i}$ 가 취하는 값은 0과 1뿐이므로 $X = X_{1} + X_{2} + \cdots + X_{n}$ 이 취할 수 있는 값은 $0, 1, 2, \cdots, n$ 이다.
- 그리고 확률 변수 `X` 는 `n` 번 독립적으로 반복 시행한 베르누이 시행에서 성공한 횟수를 나타낸다.
- 즉 `X` 는 모수 `n` 과 `p` 인 이항 분포의 확률 변수는 독립인 베르누이 확률 변수들의 합과 같다.
- 따라서 이항 분포에 따르는 확률 변수 `X` 의 평균과 분산은 다음과 같다.
$$μ = E(X_{1} + X_{2} + \cdots + X_{n}) = E(X_{1}) + E(X_{2}) + \cdots + E(X_{n}) = p + p + \cdots + p = np$$
$$σ^{2} = \text{Var}(X_{1} + X_{2} + \cdots + X_{n}) = \text{Var}(X_{1}) + \text{Var}(X_{2}) + \cdots + \text{Var}(X_{n}) = p(1-p) + p(1-p) + \cdots + p(1-p) = np(1 - p)$$
- 즉, $X \sim B(n, p)$ 의 평균과 분산은 각각 다음과 같다.
① 평균 : $μ = np$
② 분산 : $σ^{2} = npq, \; q = 1 - p$
예제 : 4지선다형으로 주어진 5문제에서 임의로 답을 선택할 때, 정답을 선택한 문제 수를 확률 변수 `X` 라 한다. 이 때, `X` 의 확률 질량 함수 `f(x)` 와 `X` 의 평균과 분산을 구하라.
각 문제당 정답을 선택할 확률은 0.25이고, 정답을 선택하는 것은 독립 시행이므로 확률 변수 `X` 는 모수 $n = 5, \; p = 0.25$ 인 이항 분포를 따른다.
따라서 `X` 의 확률 질량 함수는 다음과 같다.
$\displaystyle f(x) = \begin{cases} {}_{5}C_{x}(0.25)^{x}(0.75)^{5-x} &, x=0, 1, 2, 3, 4, 5 \\ 0 &, otherwise \end{cases}$
그리고 `X` 의 평균과 분산은 각각 $μ = 5 \times 0.25 = 1.25, \; σ^{2} = 5 \times 0.25 \times 0.75 = 0.9375$ 이다.
이항 분포와 확률
- 특히 모수 `n = 1` 과 `p` 인 이항 분포는 모수 `p` 인 베르누이 분포와 일치한다.
- 그리고 $X \sim B(n, p)$ 일 때, $a = 0, 1, \cdots, n$ 에 대해 다음과 같이 확률을 계산할 수 있다.
① $P(X = a) = P(X \le a) - P(X \le a -1)$
② $P(a < X \le b) = P(X \le b) - P(X \le a)$
③ $P(X > a) = 1 - P(X \le a)$
예제 : 4지선다형으로 주어진 5문제에서 임의로 답을 선택할 때, 정답을 선택한 문제 수를 확률 변수 `X` 라 한다. 이 때, 다음 확률을 구하라. (단, 소숫점 이하 다섯째 자리에서 반올림한다.)
(a) $P(X \le 1)$
(b) $P(X = 2)$
(c) $P(X < 3)$
(d) $P(X > 3)$
$x = 0, 1, \cdots, 5$ 에 대해 $f(x) = {}_{5}C_{x}(0.25)^{x}(0.75)^{5-x}$ 이므로 구하고자 하는 확률은 다음과 같다.
(a)
$P(X \le 1) = f(0) + f(1) = {}_{5}C_{0}(0.75)^{5} + {}_{5}C_{1}(0.25)^{1}(0.75)^{4} ≒ 0.2373 + 0.3955 = 0.6328$
(b)
$P(X = 2) = f(2) = {}_{5}C_{2}(0.25)^{2}(0.75)^{3} ≒ 0.2367$
(c)
$P(X < 3) = P(X \le 2) = f(0) + f(1) + f(2) ≒ 0.8965$
(d)
$P(X > 3) = P(X \ge 4) = f(4) + f(5) = {}_{5}C_{4}(0.25)^{4}(0.75)^{1} + {}_{5}C_{5}(0.25)^{5}(0.75)^{0} ≒ 0.0146 + 0.001 = 0.0156$
이항 분포의 확률 계산 (이항 누적 확률표 이용)
- 이항 분포에 대한 확률은 이항 누적 확률표(Cumulative Binomial Distribution Table)를 이용하여 쉽게 구할 수 있다.
- 예를 들어, $X \sim B(8, 0.45)$ 일 때 $P(X \le 4)$ 는 이항 누적 확률표를 이용하여 다음과 같이 구한다.
| ① 좌측 열에서 `n` 이 8인 부분을 선정한다. ② 상단에서 `p` 가 0.45인 열을 선택한다. ③ 좌측열에서 `x` 가 4인 행을 선택한다. ④ `x` 가 4인 행과 `p` 가 0.5인 열이 만나는 위치의 수 0.7396을 선택한다. ⑤ $P(X \le 4) = 0.7396$ 이다. |
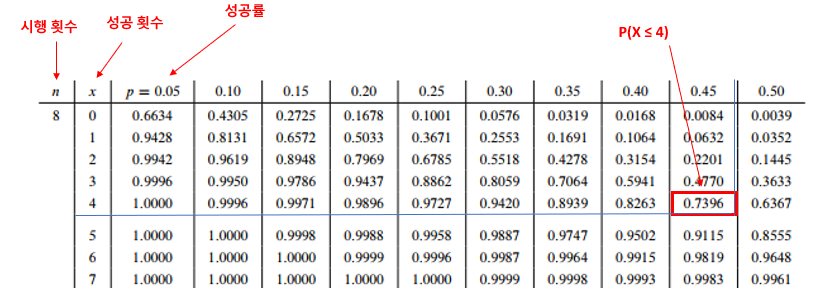
이항 누적 확률표(Cumulative Binomial Distribution Table)
이항 분포의 합성
- `X` 와 `Y` 가 독립이고, $X \sim B(m, p), \; Y \sim B(n, p)$ 라 하면, $X + Y \sim B(m + n, \; p)$ 가 성립한다.
- 일반적으로 독립인 이항 분포를 따르는 확률 변수 $X_{i} \sim B(n_{i}, \; p), \; i = 1, 2, \cdots, k$ 에 대해 다음이 성립한다.
$$X \sim B(n, p), \; 단, X = \sum_{i=1}^{k}X_{i}, \; n = \sum_{i=1}^{k}n_{i}$$
예제 : 이항 분포를 따르는 독립인 두 확률 변수 $X \sim B(3, 0.25)$ 와 $Y \sim B(5, 0.25)$ 에 대해 이항 누적 확률표를 이용하여 다음 확률을 구하라.
(a) $P(X + Y \le 4)$
(b) $P(X + Y = 4)$
(c) $P(X + Y \ge 4)$
$X \sim B(3, 0.25)$ 와 $Y \sim B(5, 0.25)$ 이고, `X` 와 `Y` 가 독립이므로 $X + Y \sim B(8, 0.25)$ 이다.
따라서 이항 누적 확률표로부터 다음을 얻는다.
(a)
$P(X + Y \le 4) = 0.9727$
(b)
$P(X + Y = 4) = P(X + Y \le 4) - P(X + Y \le 3) = 0.9727 - 0.8862 = 0.0865$
(c)
$P(X + Y \ge 4) = 1 - P(X + Y \le 3) = 1 - 0.8862 = 0.1138$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 모비율의 추정 (0) | 2022.11.28 |
|---|---|
| [확률과 통계] 모평균의 추정 (0) | 2022.11.27 |
| [확률과 통계] 모집단과 표본 (0) | 2022.11.21 |
| [확률과 통계] 연속 확률 분포 (0) | 2022.11.21 |
| [확률과 통계] 확률 변수의 평균과 분산 (0) | 2022.11.14 |
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |
| [확률과 통계] 이산 확률 변수 (0) | 2022.11.07 |
| [확률과 통계] 베이즈 정리 (0) | 2022.10.31 |


