확률
확률의 의미
- 동전 하나를 던져서 앞면이 나올 가능성을 알아보자.
- 동전을 던져서 나올 수 있는 모든 경우는 앞면(`H`)과 뒷면(`T`) 뿐이다.
- 동전을 던지는 실험에서 표본 공간은 $S = \{ H, T \}$ 이고, 앞면이 나오는 사건은 $A = \{ H \}$ 로 나타낼 수 있다.
- 이 때, `H` 와 `T` 가 모두 같은 정도로 나온다고 가정하면 사건 `A` 가 일어날 가능성은 $\frac{1}{2}$ 라고 추측할 수 있다.
- 그리고 이러한 추측에는 동전이 공정하다는 전제 조건(앞면과 뒷면이 나올 가능성이 동등하다)이 필요하다.
- 그러면 사건 `A` 가 일어날 가능성인 숫자 $\frac{1}{2}$ 에 대해, 분모의 숫자 2는 표본 공간 안의 원소의 개수이고, 분자의 숫자 1은 사건 `A` 안에 있는 원소의 개수와 일치하는 것을 알 수 있다.
- 즉, 다음과 같이 표본 공간 $S = \{ H, T \}$ 에 대해 사건 $A = \{ H \}$ 의 표본점의 비율로 생각할 수 있다.
| $$P(A) = \frac{\text{사건 A 안의 원소의 개수}}{\text{표본 공간 S 안의 원소의 개수}} = \frac{1}{2}$$ |
- 일반적으로 우연히 발생하는 어떤 사건 `A` 가 일어날 가능성은 0과 1 사이의 수, 즉 0%와 100% 사이의 값이며, 기호 $P(A)$ 로 나타낸다.
- 이 때, 표본 공간 `S` 와 사건 `A` 에 들어 있는 원소의 개수를 각각 `n(S)`, `n(A)` 로 나타낸다.
수학적 확률(Mathematical Probability)
어떤 시행에서 표본 공간 `S` 안의 모든 원소가 일어날 가능성이 동등하다고 할 때, 사건 `A` 가 일어날 확률은 다음과 같이 정의하며, 이를 수학적 확률(Mathematical Probability)이라 한다.
$$P(A) = \frac{n(A)}{n(S)}$$
예제 : 동전을 세 번 반복하여 던지는 게임을 할 때, 적어도 두 번 앞면이 나올 확률을 구하라.
표본 공간은 $S = \{ HHH, HHT, HTH, THH, HTT, THT, TTH, TTT \}$ 이고, 적어도 두 번 앞면이 나오는 사건은 $A = \{ HHH, HHT, HTH, THH \}$ 이다.
따라서 $n(S) = 8$, $n(A) = 4$ 이고, 적어도 두 번 앞면이 나올 확률은 $P(A) = \frac{4}{8} = \frac{1}{2}$ 이다.
통계적 확률(Statistical Probability)
어떤 시행을 `n` 번 반복했을 때 사건 `A` 가 일어난 횟수를 `r_{n}` 이라고 하면, `n` 이 충분히 커짐에 따라 상대도수 $\displaystyle p_{n} = \frac{r_{n}}{n}$ 은 일정한 값 `p` 에 가까워진다. 이 때, `p` 를 사건 `A` 의 통계적 확률(Statistical Probability)이라 하고, $P(A) = p$ 로 나타낸다.
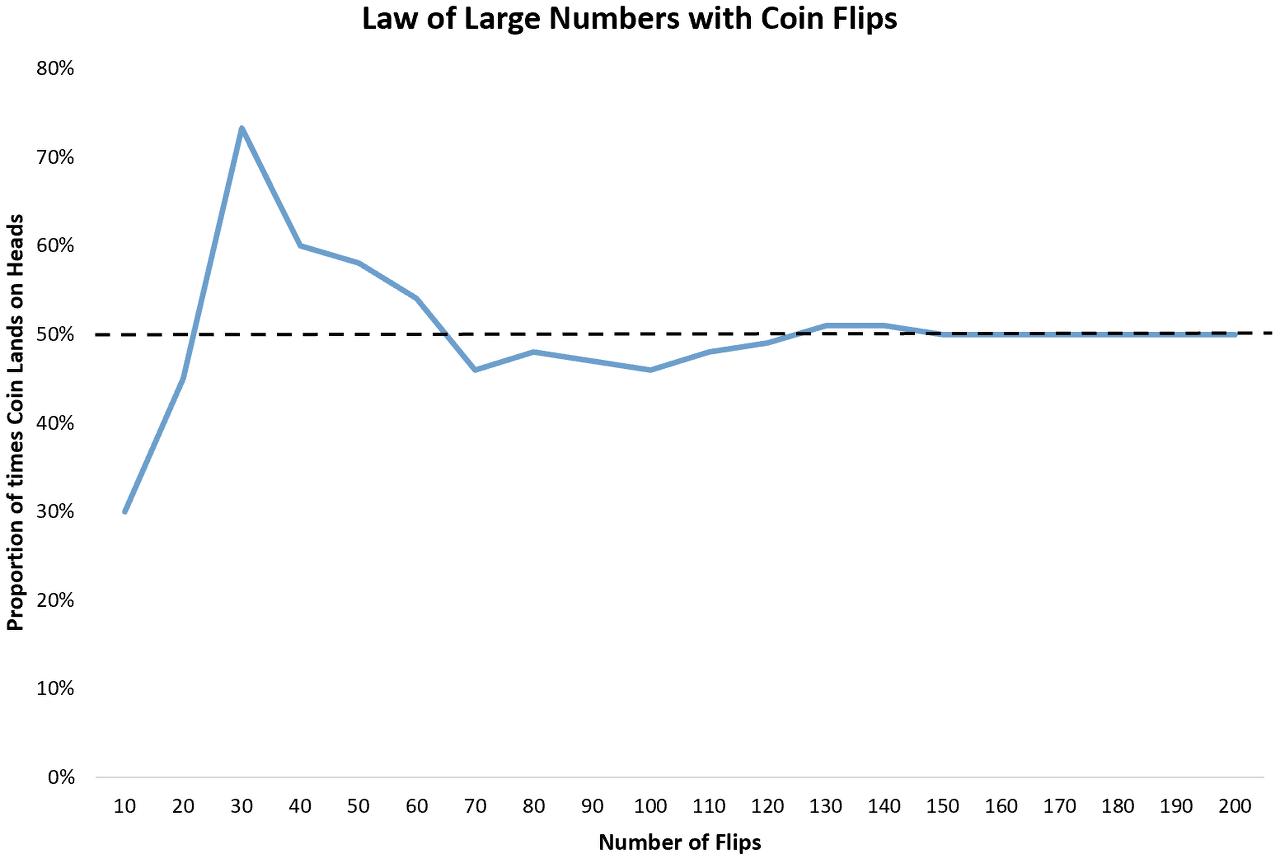
- 일반적으로 동일한 조건 아래에서 동전 던지기와 같은 동일한 시행을 반복할수록 어떤 사건의 상대 도수 $p_{n}$ 은 일정한 수 $p$ 에 가까워 진다.
- 이 때, 어떤 사건이 나타날 통계적 확률은 시행을 반복할수록 수학적 확률에 가까워지는 것을 알 수 있으며, 이것을 대수 법칙(Law of Large Numbers)이라 한다.
경험적 확률(Empirical Probability)
어떤 사건 `A` 가 발생할 확률은 경험에 의해 다음과 같이 정의하며, 이를 경험적 확률(Empirical Probability)이라 한다.
$$P(A) = \frac{\text{사건 A의 도수}}{\text{총 관찰 도수}}$$
- 경험적 확률의 예로 사람이 번개에 맞아 죽을 확률($\frac{1}{2,000,000}$), 비행기 사고로 사망할 확률($\frac{1}{11,000,000}$) 등이 있다.
- 이와 같은 확률은 모두 경험에 의한 것이다.
공리적 확률(Axiomatic Probability)
다음 3가지 공리를 만족하는 표본 공간 `S` 에서 실수로 대응하는 함수 $P(A)$ 를 사건 `A` 의 공리적 확률(Axiomatic Probability)이라 한다.
[공리 1] $P(S) = 1$
[공리 2] $A ⊂ S$ 이면, $0 ≤ P(A) ≤ 1$ 이다.
[공리 3] 쌍마다 배반인 사건 $A_{n}, \; n = 1, 2, 3, \cdots$ 에 대해 다음이 성립한다.
$$P(A_{1} ∪ A_{2} ∪ \cdots) = P(A_{1}) + P(A_{2}) + \cdots$$
- 수학적 확률의 정의는 표본 공간 안에 들어 있는 원소의 개수가 유한개이고 ,각 근원 사건이 일어날 확률이 동일한 경우에만 적용된다.
- 그러나, 궁수가 활을 쏴서 표적지에 맞출 확률을 구하는 경우와 같이 표본 공간 안의 원소의 개수가 유한하지 않은 경우에는 수학적 확률을 적용할 수 없다.
- 이러한 경우를 해소하기 위해 공리적 확률이 필요하다.
- 공리적 확률은 다음과 같은 기하학적인 의미를 갖는다.
- 영역의 크기라 함은 표본 공간이 직선인 경우는 길이를 나타내고, 평면 또는 공간인 경우에는 각각 넓이와 부피를 의미한다.
$$P(A) = \frac{\text{사건 A에 대한 영역의 크기}}{\text{표본 공간 전체 영역의 크기}}$$
예제 : 반지름의 길이가 30cm인 과녁판 중심에 반지름의 길이가 5cm인 원이 그려져 있다. 궁수가 활을 쏴서 중심에 있는 원을 맞출 확률을 구하라.
표본 공간은 반지름의 길이가 30cm인 전체 과녁판이고, 중심에 있는 반지름 5cm인 원에 맞추는 사건을 `A` 라 하자.
그러면 구하고자 하는 확률은 다음과 같다.
$\displaystyle P(A) = \frac{\text{사건 A의 넓이}}{\text{표본 공간 전체 영역의 넓이}} = \frac{5^{2}π}{30^{2}π} = \frac{1}{36}$
확률의 성질
기본 성질
- 공사건의 경우에 원소가 하나가 없으므로, 수학적 확률의 정의에 의해 다음이 성립한다.
| $$P(\varnothing) = \frac{n(\varnothing)}{n(S)} = \frac{0}{n(S)} = 0$$ |
- 표본 공간 `S` 에 대해 전체에 대한 확률은 다음과 같다.
| $$P(S) = \frac{n(S)}{n(S)} = 1$$ |
- 따라서 표본 공간과 공사건에 대해 다음 성질을 얻을 수 있다.
$$P(S) = 1, \quad P(\varnothing) = 0$$
확률의 덧셈 범칙(Addition Rule)
(1) 임의의 두 사건 `A` 와 `B` 가 배반이면, $P(A ∪ B) = P(A) + P(B)$ 이다.
(2) 임의의 두 사건 `A` 와 `B` 가 배반이 아니면, $P(A ∪ B) = P(A) + P(B) - P(A∩B)$ 이다.
- 수학적 확률의 정의는 사건을 이루는 원소의 개수와 밀접한 관계가 있다.
서로 배반인 두 사건의 합사건
- 서로 배반인 두 사건 `A` 와 `B` 의 합사건 `A ∪ B` 의 원소의 개수는 다음과 같다.
| $$n(A ∪ B) = n(A) + n(B)$$ |
- 그러므로 표본 공간 `S` 안에 들어있는 원소의 수 `n(S)` 로 양변을 나누면 다음을 얻을 수 있다.
| $$\frac{n(A∪B)}{n(S)} = \frac{n(A) + n(B)}{n(S)} = \frac{n(A)}{n(S)} + \frac{n(B)}{n(S)}$$ |
- 이 때, 좌변의 식은 합사건 $A ∪ B$ 의 확률이고, 우변의 식은 두 사건 `A` 와 `B` 의 확률 `P(A)` 와 `P(B)` 의 합이다.
- 따라서 서로 배반인 두 사건 `A` 와 `B` 의 합사건 `A ∪ B` 의 확률은 다음과 같다.
$$P(A ∪ B) = P(A) + P(B)$$
서로 배반이 아닌 두 사건의 합사건
- 서로 배반이 아닌 두 사건 `A` 와 `B` 의 합사건 `A ∪ B` 의 원소의 개수는 다음과 같다.
| $$n(A ∪ B) = n(A) + n(B) - n(A ∩ B)$$ |
- 그러므로 표본 공간 `S` 안에 들어있는 원소의 수 `n(S)` 로 양변을 나누면 다음을 얻을 수 있다.
| $$\frac{n(A∪B)}{n(S)} = \frac{n(A) + n(B) - n(A ∩ B)}{n(S)} = \frac{n(A)}{n(S)} + \frac{n(B)}{n(S)} - \frac{n(A ∩ B)}{n(S)}$$ |
- 따라서 서로 배반이 아닌 두 사건 `A` 와 `B` 의 합사건 `A ∪ B` 의 확률은 다음과 같다.
$$P(A ∪ B) = P(A) + P(B) - P(A ∩ B)$$
임의의 세 사건의 합사건
- 확률의 덧셈 법칙을 이용하면 임의의 세 사건 `A, B, C` 의 합사건의 확률을 다음과 같이 구할 수 있다.
$$P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)$$
예제 : 남자 10명과 여자 5명으로 구성된 모임에서 회장과 총무를 임의로 뽑고자 한다. 이 때, 회장과 총무가 모두 남자이거나 여자일 확률을 구하라.
회장과 총무가 모두 남자인 사건을 `A`, 모두 여자인 사건을 `B` 라 하자.
그러면 두 사건은 서로 배반이고, 전체 15명 중에서 2명을 선택하는 경우의 수는 $_{15}C_{2} = \frac{15!}{2! \times 13!} = 105$ 이다.
그리고 남자 10명과 여자 5명 중에서 각각 2명을 선택하는 경우의 수는 다음과 같다.
$_{10}C_{2} = \frac{10!}{2! \times 8!} = 45, \quad _{5}C_{2} = \frac{5!}{2! \times 3!} = 10$
그러므로 구하고자 하는 확률은 다음과 같다.
$$P(A ∪ B) = P(A) + P(B) = \frac{_{10}C_{2}}{_{15}C_{2}} + \frac{_{5}C_{2}}{_{15}C_{2}} = \frac{45}{105} + \frac{10}{105} = \frac{11}{21}$$
여사건의 확률
임의의 사건 `A` 와 여사건 `A^{C}` 에 대해 $P(A^{C}) = 1 - P(A)$ 가 성립한다.
- 표본 공간 `S` 에 대해 임의의 사건 `A` 와 $A^{C}$ 은 서로 배반이고, $A ∪ A^{C} = S$ 이다.
- 따라서 사건 `A` 와 `A^{C}` 의 원소의 개수에 대해 다음이 성립한다.
| $$n(S) = n(A ∪ A^{C}) = n(A) + n(A^{C})$$ |
- 표본 공간 `S` 의 원소의 수 `n(S)` 로 양변을 나누면 다음을 얻는다.
| $$\frac{n(A)}{n(S)} + \frac{n(A^{C})}{n(S)} = 1$$ |
- 이와 같은 여사건의 확률 공식은 직접 확률을 구하기 어려우나 여사건의 확률을 쉽게 구할 수 있는 경우 또는 '적어도' 라는 조건이 있는 확률 문제를 다룰 때 매우 편리하게 사용할 수 있다.
예제 : 10개의 배터리 중에 불량품이 3개 들어 있다. 이 중에서 동시에 4개를 꺼낼 때, 불량품이 적어도 하나 포함될 확률을 구하라.
꺼낸 배터리 4개 중에 불량품이 적어도 하나 포함되는 사건을 `A` 라 하면, `A^{C}` 은 불량품이 하나도 포함되지 않는 사건이다.
이 때, 10개의 배터리 중에서 4개를 동시에 꺼내는 방법의 수는 $_{10}C_{4} = \frac{10!}{4! \times 6!} = 210$ 이고, 불량품이 아닌 배터리 4개를 꺼내는 경우의 수는 $_{7}C_{4} = \frac{7!}{4! \times 3!} = 35$ 이다.
따라서 꺼낸 배터리 4개 중에 불량품이 하나도 포함되지 않을 확률은 다음과 같다.
$$P(A^{C}) = \frac{_{7}C_{4}}{_{10}C_{4}} = \frac{35}{210} = \frac{1}{6}$$
그러므로 꺼낸 배터리 4개 중에 불량품이 적어도 하나도 포함될 확률은 $P(A) = 1 - \frac{1}{6} = \frac{5}{6}$ 이다.
부분 사건의 확률
$A ⊂ B$ 인 임의의 두 사건 `A` 와 `B` 에 대해 다음이 성립한다.
(1) $P(B - A) = P(B) - P(A)$
(2) $P(A) ≤ P(B)$
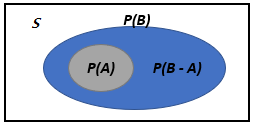
- 두 사건 `A` 와 `B` 사이에 $A ⊂ B$ 인 관계가 있는 경우에, 서로 배반인 두 사건 `A` 와 `B - A` 의 합사건을 $B = A ∪ (B - A)$ 로 표현할 수 있다.
예제 : 어느 학생이 통계학과 영어에서 A 학점을 받을 확률이 70%와 65%이고, 통계학 또는 영어에서 A 학점을 받을 확률이 86%일 때, 다음 확률을 구하라.
(a) 두 과목 모두 A를 받을 확률
(b) 통계학에서만 A를 받을 확률
(a)
통계학에서 A를 받는 사건을 `A`, 영어에서 A를 받는 사건을 `B` 라고 하자.
그러면 `P(A) = 0.7`, `P(B) = 0.65`, `P(A ∪ B) = 0.86` 이다.
그러므로 두 과목 모두 A를 받을 확률은 다음과 같다.
$$P(A ∩ B) = P(A) + P(B) - P(A∪B) = 0.7 + 0.65 - 0.86 = 0.49$$
(b)
$A ∩ B ⊂ A$ 이고, 통계학에서만 A를 받는 사건은 `A - B` 이므로, 구하고자 하는 확률은 다음과 같다.
$$P(A-B) = P(A) - P(A∩B) = 0.7 - 0.49 = 0.21$$
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 연속 확률 변수 (0) | 2022.11.14 |
|---|---|
| [확률과 통계] 이산 확률 변수 (0) | 2022.11.07 |
| [확률과 통계] 베이즈 정리 (0) | 2022.10.31 |
| [확률과 통계] 조건부 확률 (0) | 2022.10.31 |
| [확률과 통계] 시행과 사건 (0) | 2022.10.31 |
| [확률과 통계] 도수 분포표에서의 평균과 분산 (1) | 2022.10.11 |
| [확률과 통계] 위치 척도와 상자 그림 (0) | 2022.10.11 |
| [확률과 통계] 산포도 (1) | 2022.10.10 |


