728x90
위치 척도와 상자 그림
- 두 집단의 평균의 차이가 극심한 경우에는 표준 편차보다 상대적인 척도인 변동 계수를 사용한다.
- 그러나 두 집단의 평균을 일치시키고, 절대적인 수치로 주어진 자료값을 상대적인 위치로 변환할 수 있다.
- 중앙값은 가장 중앙에 놓이는 자료값이므로 자료값을 크기 순으로 나열하여 50% 위치에 놓이게 된다.
- 이 때 수집한 자료를 크기 순서로 나열하여 백등분하는 위치 또는 사등분하는 위치를 나타내는 백분위수와 사분위수를 구할 수 있다.
- 사분위수를 이용하면 특이값의 존재 여부를 명확하게 알 수 있다.
`z`-점수(`z`-Score) ; 표준 점수(Standardized Score)
각 자료의 측정값과 평균과의 편차를 표준 편차로 나눈 수치
- 자료 집단을 구성하는 개개의 자료값을 평균을 중심으로 한 상대적인 위치로 변환시킨 자료를 생각할 수 있다.
- 이와 같이 변환시킴으로써 평균이 크게 차이나는 두 집단을 상대적으로 동일하게 비교할 수 있다.
- 예) 대학수학능력시험에 대해 개개인의 원점수를 평균을 중심으로 한 상대적인 위치로 변환시킨 점수가 표준 점수이다.
- 이와 같이 변환시킴으로써 평균이 크게 차이나는 두 집단을 상대적으로 동일하게 비교할 수 있다.
- `z`-점수는 다음과 같이 구한다.
모집단의 `z`-점수 : $\displaystyle z_{i} = \frac{x_{i} - μ}{σ}$ (`μ` : 모평균, `σ` : 모 표준 편차)
표본의 `z`-점수 : $\displaystyle z_{i} = \frac{x_{i} - \overline{x}}{s}$ ($\overline{x}$ : 표본 평균, `s` : 표본 표준 편차)
- 이러한 `z`-점수는 자료 집단의 평균을 0으로 변환시키고, 평균을 중심으로 각 자료값의 절대 위치를 상대적인 위치로 변환한 값을 나타낸다.
예 : 두 표본 A [4 9 3 5 7] 과 표본 B [400 900 300 500 700]
- 두 표본 각각의 평균을 구하면 $\overline{x}_{A} = 5.6$ 이고, $\overline{x}_{B} = 560$ 으로, 두 표본을 동일한 점도표로 나타내면 비교가 되지 않는다.
- 하지만, `z`-점수를 이용하여 각 자료값의 상대적인 위치로 변환하면 다음과 같이 동일한 것을 알 수 있다.
예 : 두 표본 A [171 164 167 156 159 164], B [11.5 12.2 12.0 12.4 13.6 10.5]에 대해 다음을 구하여라.
(a) 표본 A와 표본 B의 `z`-점수
(b) `z`-점수에 대한 점도표
(c) 변동 계수의 결과와 비교하기
더보기
두 표본 A와 B의 평균을 $\overline{x}, \overline{y}$ 라 하고, 표준 편차를 $s_{A}, s_{B}$ 라 하면,
$\displaystyle \overline{x} = \frac{171 + 164 + 167 + 156 + 159 + 164}{6} = 163.5$
$\displaystyle \overline{y} = \frac{11.5 + 12.2 + 12 + 12.4 + 13.6 + 10.5}{6} ≒ 12$
$\displaystyle s^{2}_{A} = \frac{1}{5} \sum(x - 163.5)^{2} = 29.1$
$\displaystyle s_{A} = \sqrt{29.1} ≒ 5.39$
$\displaystyle s^{2}_{B} = \frac{1}{5} \sum(x - 12)^{2} = 1.052$
$\displaystyle s_{B} = \sqrt{1.052} ≒ 1.026$
이다. 두 표본의 변동 계수를 구하면 각각 다음과 같다.
$\displaystyle C.V_{A} = \frac{5.39}{163.5} ≒ 0.033, \quad C.V_{B} = \frac{1.026}{12} ≒ 0.0855$
(a)
$\overline{x} = 163.5, \; \overline{y} = 12, \; s_{A} = 5.39, \; s_{B} = 1.026$ 이다.
표본 A의 각 자료값에 $\displaystyle z_{i} = \frac{x_{i} - 163.5}{5.39}$ 를 이용하면 다음을 얻는다.
표본 B의 각 자료값에 $\displaystyle z_{i} = \frac{y_{i} - 12}{1.026}$ 를 이용하면 다음을 얻는다.
(b)
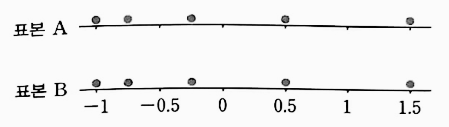
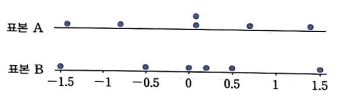
두 표본의 `z`-점수에 대한 점도표를 그리면 다음과 같다.
$\displaystyle \overline{x} = \frac{171 + 164 + 167 + 156 + 159 + 164}{6} = 163.5$
$\displaystyle \overline{y} = \frac{11.5 + 12.2 + 12 + 12.4 + 13.6 + 10.5}{6} ≒ 12$
$\displaystyle s^{2}_{A} = \frac{1}{5} \sum(x - 163.5)^{2} = 29.1$
$\displaystyle s_{A} = \sqrt{29.1} ≒ 5.39$
$\displaystyle s^{2}_{B} = \frac{1}{5} \sum(x - 12)^{2} = 1.052$
$\displaystyle s_{B} = \sqrt{1.052} ≒ 1.026$
이다. 두 표본의 변동 계수를 구하면 각각 다음과 같다.
$\displaystyle C.V_{A} = \frac{5.39}{163.5} ≒ 0.033, \quad C.V_{B} = \frac{1.026}{12} ≒ 0.0855$
(a)
$\overline{x} = 163.5, \; \overline{y} = 12, \; s_{A} = 5.39, \; s_{B} = 1.026$ 이다.
표본 A의 각 자료값에 $\displaystyle z_{i} = \frac{x_{i} - 163.5}{5.39}$ 를 이용하면 다음을 얻는다.
| 자료값 | 171 | 164 | 167 | 156 | 159 | 164 |
| `z`-점수 | 1.39 | 0.09 | 0.65 | -1.39 | -0.83 | 0.09 |
표본 B의 각 자료값에 $\displaystyle z_{i} = \frac{y_{i} - 12}{1.026}$ 를 이용하면 다음을 얻는다.
| 자료값 | 11.5 | 12.2 | 12.0 | 12.4 | 13.6 | 10.5 |
| `z`-점수 | -0.49 | 0.19 | 0.00 | 0.39 | 1.56 | -1.46 |
(b)
두 표본의 `z`-점수에 대한 점도표를 그리면 다음과 같다.

(c)
변동 계수에 의한 결과와 동일하게, 표본 B가 표본 A에 비해 상대적으로 넓게 분포한다.
백분위수(Percentile)와 사분위수(Quartiles)
- 백분위수(Percentile) : 수집한 자료를 크기순으로 나열할 때, 1% 씩 등간격으로 구분하는 척도 $P_{1}, P_{2}, \cdots, P_{99}$
- 사분위수(Quartiles) : 수집한 자료를 크기순으로 나열하여 4등분하는 척도 $Q_{1}, Q_{2}, Q_{3}$
- 수집한 자료를 크기순으로 나열하여 백등분하는 위치를 나타내는 척도와 사등분하는 위치를 나타내는 척도를 이용하는 경우가 종종 있다.
- 예) 대학수학능력시험에 대한 개개인의 원점수와 백분위 점수
- 백분위 점수는 전체 시험 응시자의 원점수를 백등분한 점수를 의미한다.
- 예) 대학수학능력시험에 대한 개개인의 원점수와 백분위 점수
- 사분위수는 전체 자료를 4등분하는 척도이므로, 다음의 백분위수와 같다.
- 제1 사분위수 `Q_{1}` = 제25 백분위수 `P_{25}`
- 제2 사분위수 `Q_{2}` = 제50 백분위수 `P_{50}` = 중앙값 `M_{e}`
- 제3 사분위수 `Q_{3}` = 제75 백분위수 `P_{75}`
백분위수 구하기
- `n` 개의 자료로 구성된 자료 집단의 `k`-백분위수 `P_{k}` 는 다음과 같은 순서로 구한다.
① 자료값을 가장 작은 수부터 크기순으로 재배열한다.
② $\displaystyle m = \frac{kn}{100}$ 을 계산한다.
③ 이때 `m` 이 정수인지 아닌지에 따라 `P_{k}` 를 다음과 같이 구한다.
- `m` 이 정수이면, `P_{k}` 는 다음과 같이 `m` 번째와 `m + 1` 번째 위치하는 자료값의 평균이다.
- `m` 이 정수가 아니면, `P_{k}` 는 `m` 보다 큰 정수에서 가장 작은 정수에 해당하는 위치의 자료값이다.
$\displaystyle P_{k} = \frac{x_{(m)} + x_{(m + 1)}}{2}$
예제 : 다음 표본에 대한 사분위수를 구하라.
| 26 | 31 | 27 | 38 | 42 | 26 | 18 | 17 | 25 | 29 |
| 39 | 38 | 38 | 40 | 46 | 38 | 39 | 41 | 41 | 40 |
| 26 | 19 | 39 | 28 | 45 | 34 | 21 | 41 | 30 | 30 |
| 12 | 22 | 48 | 34 | 29 | 26 | 29 | 58 | 43 | 16 |
| 42 | 44 | 38 | 44 | 28 | 43 | 39 | 42 | 39 | 46 |
더보기
표본을 다음과 같이 크기순으로 재배열한다.
| 12 | 16 | 17 | 18 | 19 | 21 | 22 | 25 | 26 | 26 |
| 26 | 26 | 27 | 28 | 28 | 29 | 29 | 29 | 30 | 30 |
| 31 | 34 | 34 | 38 | 38 | 38 | 38 | 38 | 39 | 39 |
| 39 | 39 | 39 | 40 | 40 | 41 | 41 | 41 | 42 | 42 |
| 42 | 43 | 43 | 44 | 44 | 45 | 46 | 46 | 48 | 58 |
`n = 50` 이고 사분위수의 위치는 각각 `k = 25, 50, 75` 이므로 사분위수를 구하면 다음과 같다.
제1 사분위수 : $\displaystyle m = \frac{50 × 25}{100} = 12.5 \Rightarrow Q_{1} = P_{25} = x_{13} = 27$
제2 사분위수 : $\displaystyle m = \frac{50 × 50}{100} = 25 \Rightarrow Q_{2} = P_{50} = \frac{x_{(25)} + x_{(26)}}{2} = \frac{38 + 38}{2} = 38$
제3 사분위수 : $\displaystyle m = \frac{50 × 75}{100} = 37.5 \Rightarrow Q_{3} = P_{75} = x_{38} = 41$
상자 그림(Box Plot)
사분위수 범위(Interquartile Range; I.Q.R)
수집한 자료의 제1 사분위수와 제3 사분위수인 `Q_{1}` 과 `Q_{3}` 사이의 범위를 의미하며 `I.Q.R` 로 표현한다.
$I.Q.R = Q_{3} - Q_{1}$
- 대푯값으로 중앙값을 사용하는 경우에 특이값의 영향을 받지 않는 범위로 사분위수 범위를 많이 사용한다.
- 사분위수 범위는 아래쪽과 위쪽으로부터 각각 25%의 자료를 제거한 범위이므로 특이값의 영향을 전혀 받지 않는다.
예제 : <백분위수 구하기> 예제의 자료에 대한 사분위수 범위를 구하라.
더보기
$Q_{1} = 27, \; Q_{3} = 41$ 을 구했으므로, 사분위수 범위는 다음과 같다.
$I.Q.R = 41 - 27 = 14$
상자 그림(Box Plot)
사분위수를 이용하여 수집한 자료에 포함된 특이값을 알려주는 그림
- 사분위수를 이용하면 수집한 자료 집단의 중심부 50% 안에 놓이는 자료의 분포 모양과 꼬리 부분의 상태를 비롯하여 특이값을 나타내는 상자 그림을 그릴 수 있다.
상자 그림의 특징
- 상자 그림은 대푯값으로 중앙값을 사용하며, 다음과 같은 특징을 갖는다.
① 특이값에 대한 정보를 제공한다.
② 자료의 중심 위치와 흩어진 모양, 그리고 분포의 꼬리 부분을 쉽게 파악할 수 있다.
③ 상자 그림은 2개 이상의 자료 집단을 비교할 때 매우 유용하다.
용어 정리
- 안 울타리(Inner Fence)
- 사분위수 `Q_{1}` 과 `Q_{3}` 에서 각각 $1.5 × I.Q.R$ 만큼 떨어져 있는 값
- 아래쪽 안 울타리(Lower Inner Fence) : $f_{l} = Q_{1} - 1.5 × I.Q.R$
- 위쪽 안 울타리(Upper Inner Fence) : $f_{u} = Q_{3} + 1.5 × I.Q.R$
- 바깥 울타리(Outer Fence)
- 사분위수 `Q_{1}` 과 `Q_{3}` 에서 각각 $3 × I.Q.R$ 만큼 떨어져 있는 값
- 아래쪽 바깥 울타리(Lower Outer Fence) : $f_{L} = Q_{1} - 3 × I.Q.R$
- 위쪽 바깥 울타리(Upper Outer Fence) : $f_{U} = Q_{3} + 3 × I.Q.R$
- 인접값(Adjacent Value)
- 안 울타리 안에 놓이는 가장 극단적인 자료값
- 아래쪽 안 울타리보다 큰 자료값 중에서 가장 작은 자료값
- 위쪽 안 울타리보다 작은 자료값 중에서 가장 큰 자료값
- 보통 특이값(Mild Outlier)
- 안 울타리와 바깥 울타리 사이에 놓이는 자료값
- 특이값(Extreme Outlier)
- 바깥 울타리 외부에 놓이는 자료값
상자 그림 그리기
- 상자 그림은 다음 순서에 따라 그린다.
① 자료를 크기순으로 나열하여 사분위수 `Q_{1}, Q_{2}, Q_{3}` 를 구한다.
② 사분위수 범위 $I.Q.R = Q_{3} - Q_{1}$ 을 구한다.
③ `Q_{1}` 에서 `Q_{3}` 까지 직사각형 모양의 상자를 그리고, 중위수 `Q_{2}` 위치인 상자 안에 수직선을 긋는다.
④ 안 울타리를 구하고 인접값에 기호 '|' 로 표시한 후, 각각 `Q_{1}` 과 `Q_{3}` 으로부터 인접값까지 선분으로 연결하여 상자 그림의 날개 부분을 작성한다.
⑤ 바깥 울타리를 구하여 관측 가능한 보통 특이값의 위치에 '○', 특이값의 위치에 'x' 로 표시한다.
- 이러한 순서에 따라 상자 그림을 그리면 다음을 얻는다.
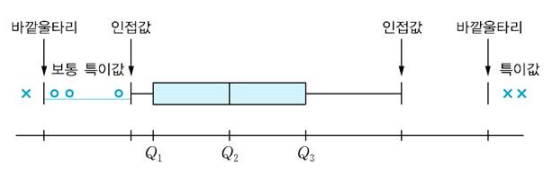
- 이 그림으로부터 다음 사실을 쉽게 알 수 있다.
- 중앙값을 중심으로 중심부 50% 자료는 대칭성을 갖는다.
- 아래쪽 날개 부분이 위쪽보다 짧다. 즉 자료의 분포에서 아래쪽 꼬리 부분보다 위쪽 꼬리 부분이 길게 분포한다.
- 측정 가능한 보통 특이값이 3개이고, 특성값이 3개 있다.
728x90
'Mathematics > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 조건부 확률 (0) | 2022.10.31 |
|---|---|
| [확률과 통계] 확률 (0) | 2022.10.31 |
| [확률과 통계] 시행과 사건 (0) | 2022.10.31 |
| [확률과 통계] 도수 분포표에서의 평균과 분산 (1) | 2022.10.11 |
| [확률과 통계] 산포도 (1) | 2022.10.10 |
| [확률과 통계] 대푯값 (0) | 2022.10.10 |
| [확률과 통계] 양적 자료의 정리 (0) | 2022.10.04 |
| [확률과 통계] 질적 자료의 정리 (0) | 2022.10.04 |


