728x90
728x90
문제
영선이는 길이가 a, b, c인 세 막대를 가지고 있고, 각 막대의 길이를 마음대로 줄일 수 있다.
영선이는 세 막대를 이용해서 아래 조건을 만족하는 삼각형을 만들려고 한다.
- 각 막대의 길이는 양의 정수이다
- 세 막대를 이용해서 넓이가 양수인 삼각형을 만들 수 있어야 한다.
- 삼각형의 둘레를 최대로 해야 한다.
a, b, c가 주어졌을 때, 만들 수 있는 가장 큰 둘레를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 a, b, c (1 ≤ a, b, c ≤ 100)가 주어진다.
출력
첫째 줄에 만들 수 있는 가장 큰 삼각형의 둘레를 출력한다.
예제 입력 1
1 2 3
예제 출력 1
5
예제 입력 2
2 2 2
예제 출력 2
6
예제 입력 3
1 100 1
예제 출력 3
3
예제 입력 4
41 64 16
예제 출력 4
113
알고리즘 분류
- 수학
- 구현
- 기하학
문제 출처
https://www.acmicpc.net/problem/14215
14215번: 세 막대
첫째 줄에 a, b, c (1 ≤ a, b, c ≤ 100)가 주어진다.
www.acmicpc.net
문제 해결 방법
- 삼각형의 결정 조건을 알면 쉽게 풀 수 있는 문제였다. (삼각형의 결정 조건에 대한 자세한 설명은 아래의 참고 항목을 확인한다.)
- 3개의 변이 주어질 경우, 삼각형의 결정 조건은 가장 긴 변의 길이가 다른 두 변의 길이의 합보다 작아야 한다는 것이다.
- 그리고 문제에서 각 막대의 길이를 마음대로 조절할 수 있다고 제시되어 있으므로, 이 문제는 "주어진 3개의 막대 길이를 이용하여 삼각형의 결정 조건을 만족시킬 수 있도록 하라."라는 문제와 동일하다고 볼 수 있다.
- 따라서 우선 막대 길이의 최솟값(@minNum@)과 최댓값(@maxNum@)을 구한 후, 삼각형의 결정 조건을 만족할 경우 세 막대 길이의 합을 출력해 주고, 그렇지 않을 경우 막대 길이의 최댓값(@maxNum@)의 길이를 삼각형의 결정 조건을 만족시키도록 조절한 후 세 막대 길이의 합을 출력해주면 된다.
- 막대 길이의 최댓값(@maxNum@)은 삼각형의 결정 조건을 만족시킬 만큼만 길이를 줄여준다.
- 즉, @maxNum@을 $(\text{minNum} + \text{num}) - 1$로 만들어주면 된다.
- 따라서 @maxNum@은 @minNum + num@ 보다 @1@이 작아지게 될 것이고, 삼각형의 결정 조건을 만족시키게 된다. 또한, 이렇게 된다면 삼각형의 결정 조건을 만족시킴과 동시에 세 막대의 길이의 합이 최댓값이 될 것이다.
- 문제에서 주어진 예제를 활용하여 이 과정을 적용시켜보면 다음과 같다.
(1) 41 64 16
64 > 16 + 41 = 57
▼ (-8)
56 (= 57 - 1)
=> 56 + 57 = 113
(2) 1 100 1
100 > 1 + 1 = 2
▼ (-99)
1 (= 2 - 1)
=> 1 + 2 = 3
(3) 2 2 2
2 < 2 + 2 = 4
=> 2 + 2 + 2 = 6
- 위의 과정을 코드로 작성하면 다음과 같다.
int Solution(int s1, int s2, int s3) {
int sum, minNum, num, maxNum;
// 삼각형의 결정 조건 : 가장 긴 변의 길이가 다른 두 변의 길이의 합보다 작아야 한다.
lengths.push_back(s1);
lengths.push_back(s2);
lengths.push_back(s3);
// 오름차순 정렬
sort(lengths.begin(), lengths.end());
maxNum = lengths[2];
num = lengths[1];
minNum = lengths[0];
if (minNum + num > maxNum) {
sum = minNum + num + maxNum;
}
else {
sum = (minNum + num) * 2 - 1;
}
return sum;
}
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int a, b, c;
vector<int> lengths;
void Input() {
cin >> a >> b >> c;
}
int Solution(int s1, int s2, int s3) {
int sum, minNum, num, maxNum;
// 삼각형의 결정 조건 : 가장 긴 변의 길이가 다른 두 변의 길이의 합보다 작아야 한다.
lengths.push_back(s1);
lengths.push_back(s2);
lengths.push_back(s3);
// 오름차순 정렬
sort(lengths.begin(), lengths.end());
maxNum = lengths[2];
num = lengths[1];
minNum = lengths[0];
if (minNum + num > maxNum) {
sum = minNum + num + maxNum;
}
else {
sum = (minNum + num) * 2 - 1;
}
return sum;
}
void Output() {
cout << Solution(a, b, c) << '\n';
}
void Solve() {
Input();
Output();
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
Solve();
return 0;
}
채점 결과

참고
- [단계별로 풀어보기] > [기하: 직사각형과 삼각형]
- 브론즈 III
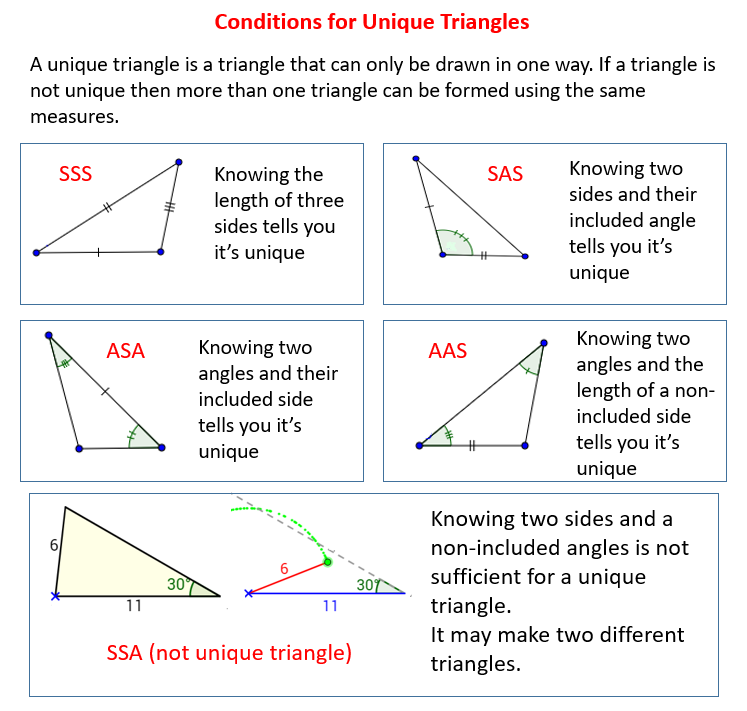
삼각형의 결정 조건
- 다음과 같이 3가지 경우에 따라 삼각형의 결정 조건이 달라진다.
① 세 변의 길이를 알 경우
→ 가장 긴 변의 길이가 다른 두 변의 길이의 합보다 작아야 한다.
② 두 변의 길이와 그 사이 끼인각의 크기를 알 경우
③ 한 변의 길이와 양쪽 끝각의 크기를 알 경우
728x90
728x90
'Problem Solving > BOJ' 카테고리의 다른 글
| [BOJ-24262][C++] 알고리즘 수업 - 알고리즘의 수행 시간 1 (0) | 2023.06.25 |
|---|---|
| [BOJ-24265][C++] 알고리즘 수업 - 알고리즘의 수행 시간 4 (0) | 2023.06.24 |
| [BOJ-24264][C++] 알고리즘 수업 - 알고리즘의 수행 시간 3 (0) | 2023.06.23 |
| [BOJ-24263][C++] 알고리즘 수업 - 알고리즘의 수행 시간 2 (0) | 2023.06.22 |
| [BOJ-9063][C++] 대지 (0) | 2023.06.20 |
| [BOJ-2903][C++] 중앙 이동 알고리즘 (0) | 2023.06.19 |
| [BOJ-2720][C++] 세탁소 사장 동혁 (0) | 2023.06.18 |
| [BOJ-11005][C++] 진법 변환 2 (0) | 2023.06.17 |
