728x90
728x90
그래프의 활용
- 네트워크의 데이터 흐름이나 스케줄링, 논리회로 설계, 정렬, 탐색, 인공지능의 지식 정보 생성 과정 등 그리고 실생활에서 많이 접할 수 있는 도로망 설계나 버스 및 지하철 노선 설계 등과 같이 어떤 문제를 해결하기 위한 모델링 과정에서 그래프 이론은 매우 중요하게 쓰인다.
- 이러한 모델링에서 최단 경로를 구하거나 정보 탐색을 하는 방법이 많이 쓰인다.
최단 경로 문제(Shortest Path Problem)
$|E| > 0$ 인 연결 그래프 $G = (V, \; E)$ 에서 정점 $v_{1}, v_{2} \in V$ 간의 가장 짧은 거리의 경로를 찾는 문제
- 지도의 어떤 지역 A에서 다른 지역 B로 이동하는 경로나, 네트워크의 어떤 호스트 A에서 다른 호스트 B로 이동하는 경로는 다양할 수 있다.
- 이렇게 찾을 수 있는 다양한 경로 중에서 가장 효과적인 경로를 선택하여 이동하거나 활용할 것이다.
- 최단 경로 문제는 이러한 예들처럼 다양한 경로 중 가장 비용이 적게 들고 빠르게 이동할 수 있는 경로를 찾는 문제이다.
- 최단 경로 문제를 고려할 때 일반적으로 가중치 방향 그래프를 사용하여 경로에 포함된 가중치의 합을 이용해 최단 거리를 판단하지만, 가중치 그래프가 제공되지 않는 경우에는 경로의 길이로 판단한다.
- 가중치 방향 그래프로 최단 거리를 판단할 경우 가중치의 의미는 매우 중요하다.
- 가중치가 정점 $v_{1}$ 에서 정점 $v_{2}$ 로 가는 비용일 경우 가중치의 합이 가장 작은 경로가 최단 거리이지만, 효과일 경우에는 가중치의 합이 가장 큰 경로가 최단 거리이다.
- 이 페이지에서는 가중치의 의미를 비용으로 하고 최단 경로 문제를 다룬다.
예 : 그래프에서 정점 `a` 에서 정점 `e` 로의 최단 경로 구하기

- 정점 `a` 에서 정점 `e` 로의 경로는 다음과 같이 6가지 경로가 존재하며, 각 경로의 가중치도 다음과 같다.
| ① `a - b - c - d - e` : 15 + 17 + 2 + 3 = 37 ② `a - b - c - e` : 15 + 17 + 10 = 42 ③ `a - f - b - c - d - e` : 2 + 10 + 17 + 2 + 3 = 34 ④ `a - f - b - c - e` : 2 + 10 + 17 + 10 = 39 ⑤ `a - f - h - e` : 2 + 14 + 17 = 33 ⑥ `a - f - g - h - e` : 2 + 9 + 10 + 17 = 38 |
- 전체에서 가중치는 비용이라고 했으므로, 그래프에서 최단 경로는 ⑤이다.
다익스트라 알고리즘(Dijkstra Algorithm)
시작하는 정점으로부터 최단 경로를 갖는 정점을 차례로 탐색하는 최단 경로 탐색 알고리즘
- 다익스트라 알고리즘은 최단 경로 문제를 해결하는 가장 대표적인 알고리즘으로, 네덜란드의 컴퓨터 과학자 에츠허르 비버 다익스트라(Edsger Wybe Dijkstra)가 제안하였다.

기호 정의
- 규정된 기호는 아직 없으나 설명을 위해 이 페이지에서는 다음과 같이 기호를 정의한다.
- 연결된 가중치 방향 그래프 $G = <V, \; E>$ 에서 $V = \{v_{1}, v_{2}, \cdots, v_{n} \}$ 이고 시작 정점을 $v_{1}$ 이라 가정할 때 다음과 같다.
| - $C[v_{i}, \; v_{j}]$ : 정점 $v_{i}$ 에서 정점 $v_{j}$ 로 가는 각 변의 가중치 - $D[v_{i}]$ : 시작 정점 $v_{1}$ 에서 정점 $v_{i}$ 까지 이르는 변들의 가중치의 합, 정점 $v_{1}$ 에서 정점 $v_{j}$ 로 가는 경로가 없으면 그 가중치는 $\infty$ 로 나타낸다. - 집합 `S` : 최단 경로에 선택된 정점의 집합 |
- 다익스트라 알고리즘은 시작 정점에서부터 정점을 차례로 탐색하면서 $D[v_{i}]$ 가 가장 작은 값이 되는 정점을 집합 `S` 에 반복하여 포함해서 그래프 `G` 의 정점 집합 `V` 와 상등이면(`S = V`) 알고리즘이 종료된다.
예 : 다익스트라 알고리즘을 이용하여 그래프의 최단 경로 찾아보기

- 이 그래프에서 각 변의 가중치는 다음과 같다.
| $C[a, b] = 15$ | $C[a, f] = 2$ | $C[b, c] = 17$ | $C[c, d] = 2$ |
| $C[c, e] = 10$ | $C[d, e] = 3$ | $C[f, b] = 10$ | $C[f, g] = 9$ |
| $C[f, h] = 14$ | $C[g, h] = 10$ | $C[h, e] = 17$ |
(1) 초기 단계
- 탐색 전 정점 집합은 $V_{S} = \{ a, b, c, d, e, f, g, h \}$ 이다.
- $S = \varnothing$
- 경로 탐색 전이므로 시작 정점에서 다른 정점에 이르는 변의 가중치 합은 모두 $\infty$ 로 초기화한다.
| $D[a] = \infty$ | $D[b] = \infty$ | $D[c] = \infty$ | $D[d] = \infty$ |
| $D[e] = \infty$ | $D[f] = \infty$ | $D[g] = \infty$ | $D[h] = \infty$ |
(2) 시작 정점을 `a` 로 설정
- 탐색 전 정점 집합은 $V_{S} = \{ b, c, d, e, f, g, h \}$ 이다.
- $S = \{ a \}$
- 시작 정점 `a` 에서부터 그래프 `G` 내의 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, b] = 15$ | $D[c] = C[a, c] = \infty$ | $D[d] = C[a, d] = \infty$ | $D[e] = C[a, e] = \infty$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, g] = \infty$ | $D[h] = C[a, h] = \infty$ |
(3) (2)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `f` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ b, c, d, e, g, h \}$ 이다.
- $S = \{ a, f \}$
- 정점 `f` 를 추가했으므로 시작 정점 `a` 부터 정점 `f` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, c] = \infty$ | $D[b] = C[a, f] + C[f, d] = \infty$ |
| $D[e] = C[a, f] + C[f, e] = \infty$ | $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
- $D[b]$ 의 경우 `<a, b>` 의 가중치 15보다 정점 `f` 를 거쳐서 가는 `<a, f>, <f, b>` 의 가중치 합 12가 작으므로 더 작은 가중치인 12를 고려한다.
(4) (3)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `g` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ b, c, d, e, h \}$ 이다.
- $S = \{ a, f, g \}$
- 정점 `g` 를 추가했으므로 시작 정점 `a` 부터 정점 `g` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, g] + C[g, c] = \infty$ |
| $D[d] = C[a, f] + C[f, g] + C[g, d] = \infty$ | $D[e] = C[a, f] + C[f, g] + C[g, e] = \infty$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
- $D[h]$ 의 경우 정점 `g` 를 거쳐서 가는 `<a, f>, <f, g>, <g, h>` 의 가중치 합 21보다 $<a, f>, <f, h>$ 의 가중치 합 16이 더 작으므로 더 작은 가중치 16을 고려한다.
(5) (4)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `b` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ c, d, e, h \}$ 이다.
- $S = \{ a, f, g, b \}$
- 정점 `b` 를 추가했으므로 시작 정점 `a` 부터 정점 `b` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, b] + C[b, c] = 29$ |
| $D[d] = C[a, f] + C[f, b] + C[b, d] = \infty$ | $D[e] = C[a, f] + C[f, b] + C[b, e] = \infty$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
(6) (5)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `h` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ c, d, e \}$ 이다.
- $S = \{ a, f, g, b, h \}$
- 정점 `h` 를 추가했으므로 시작 정점 `a` 부터 정점 `h` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, b] + C[b, c] = 29$ |
| $D[d] = C[a, f] + C[f, h] + C[h, d] = \infty$ | $D[e] = C[a, f] + C[f, h] + C[h, e] = 33$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
(7) (6)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `c` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ d, e \}$ 이다.
- $S = \{ a, f, g, b, h, c \}$
- 정점 `c` 를 추가했으므로 시작 정점 `a` 부터 정점 `c` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, b] + C[b, c] = 29$ |
| $D[d] = C[a, f] + C[f, b] + C[b, c] + C[c, d] = 31$ | $D[e] = C[a, f] + C[f, h] + C[h, e] = 33$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
- $D[e]$ 의 경우, 정점 `c` 를 거쳐서 가는 `<a, f>, <f, b>, <b, c>, <c, e>` 의 가중치 합 39 보다 `<a, f>, <f, h>, <h, e>` 의 가중치 합 33이 작으므로 더 작은 가중치인 33을 고려한다.
(8) (7)단계에서 가중치의 합이 최소인 변에 해당하는 정점 `d` 를 선택
- 탐색 전 정점 집합은 $V_{S} = \{ e \}$ 이다.
- $S = \{ a, f, g, b, h, c, d \}$
- 정점 `d` 를 추가했으므로 시작 정점 `a` 부터 정점 `d` 를 거쳐 다른 정점으로 가는 경로의 가중치 합을 계산하면 다음과 같다.
| $D[b] = C[a, f] + C[f, b] = 12$ | $D[c] = C[a, f] + C[f, b] + C[b, c] = 29$ |
| $D[d] = C[a, f] + C[f, b] + C[b, c] + C[c, d] = 31$ | $D[e] = C[a, f] + C[f, h] + C[h, e] = 33$ |
| $D[f] = C[a, f] = 2$ | $D[g] = C[a, f] + C[f, g] = 11$ |
| $D[h] = C[a, f] + C[f, h] = 16$ |
- $D[e]$ 의 경우, 정점 `c` 를 거쳐서 가는 `<a, f>, <f, b>, <b, c>, <c, e>` 의 가중치 합 39 나 `<a, f>, <f, b>, <b, c>, <c, d>, <d, e>` 의 가중치 합 34 보다 `<a, f>, <f, h>, <h, e>` 의 가중치 합 33이 작으므로 더 작은 가중치인 33을 고려한다.
(9) 더 이상 고려할 가중치가 없으므로 남은 정점 `e` 를 집합 `S` 에 포함한다.
- 탐색 전 정점 집합은 $V_{S} = \varnothing $ 이다.
- $S = \{ a, f, g, b, h, c, d, e \}$
(1)부터 (9)까지의 풀이 과정을 표로 정리하면 다음과 같다.
| 단계 | 탐색 전 최단 경로 집합(`S`)과 남은 정점 집합($V_{S}$) |
D[b] | D[c] | D[d] | D[e] | D[f] | D[g] | D[h] | 최단 경로 정점 |
탐색 후 최단 경로 집합(`S`)과 남은 정점 집합($V_{S}$) |
| (1) | $V_{S} = \{a, b, c, d, e, f, g, h \}$ $S = \varnothing$ |
`∞` | `∞` | `∞` | `∞` | `∞` | `∞` | `∞` | `a` | $V_{S} = \{ b, c, d, e, f, g, h \}$ $S = \{ a \}$ |
| (2) | $V_{S} = \{ b, c, d, e, f, g, h \}$ $S = \{ a \}$ |
`15` | `∞` | `∞` | `∞` | `2` | `∞` | `∞` | `f` | $V_{S} = \{ b, c, d, e, g, h \}$ $S = \{ a, f \}$ |
| (3) | $V_{S} = \{ b, c, d, e, g, h \}$ $S = \{ a, f \}$ |
`12` | `∞` | `∞` | `∞` | `2` | `11` | `16` | `g` | $V_{S} = \{ b, c, d, e, h \}$ $S = \{ a, f, g \}$ |
| (4) | $V_{S} = \{ b, c, d, e, h \}$ $S = \{ a, f, g \}$ |
`12` | `∞` | `∞` | `∞` | `2` | `11` | `16` | `b` | $V_{S} = \{ c, d, e, h \}$ $S = \{ a, f, g, b \}$ |
| (5) | $V_{S} = \{ c, d, e, h \}$ $S = \{ a, f, g, b \}$ |
`12` | `29` | `∞` | `33` | `2` | `11` | `16` | `h` | $V_{S} = \{ c, d, e \}$ $S = \{ a, f, g, b, h \}$ |
| (6) | $V_{S} = \{ c, d, e \}$ $S = \{ a, f, g, b, h \}$ |
`12` | `29` | `∞` | `33` | `2` | `11` | `16` | `c` | $V_{S} = \{ d, e \}$ $S = \{ a, f, g, b, h, c \}$ |
| (7) | $V_{S} = \{ d, e \}$ $S = \{ a, f, g, b, h, c \}$ |
`12` | `29` | `31` | `33` | `2` | `11` | `16` | `d` | $V_{S} = \{ e \}$ $S = \{ a, f, g, b, h, c, d \}$ |
| (8) | $V_{S} = \{ e \}$ $S = \{ a, f, g, b, h, c, d \}$ |
`12` | `29` | `31` | `33` | `2` | `11` | `16` | `e` | $V_{S} = \varnothing $ $S = \{ a, f, g, b, h, c, d, e \}$ |
- 이와 같은 과정을 통해 시작 정점으로부터 각 정점까지의 최단 경로를 찾을 수 있다.
다익스트라 알고리즘
Dijkstra(V) {
탐색한 원소 리스트 S에 정점 v1 추가;
탐색해야 할 원소 리스트 Vs에 V - {v1} 원소를 차례로 추가;
for (vi ∈ Vs) {
D[vi] = ∞;
}
while (vx ∈ V) {
if (min(D[vx])) {
리스트 S의 마지막에 vx 추가;
리스트 Vs에서 vx 제거;
}
for (vx 에 인접한 vy ∈ V) {
D[vy] = min(D[vy], D[vx] + C[vx, vy]);
}
}
}
그래프 탐색
- 그래프에 표시된 모든 지역을 탐색하는 방법은 다양하지만, 시작 정점을 기준으로 일정한 방향으로 탐색하는 방법이 가장 효율적일 수 있다.
- 그래프 탐색의 대표적인 두 방법으로 깊이 우선 탐색(DFS; Depth First Search)과 너비 우선 탐색(BFS; Breadth First Search)가 있다.
깊이 우선 탐색(DFS; Depth First Search)
연결 그래프 $G = (V, \; E)$ 에 포함되는 어떤 정점 $v_{1}$ 을 시작 정점으로 할 때, $v_{1}$ 에 인접한 정점 중 아직 탐색하지 않은 정점 $v_{2}$ 를 탐색하고, 정점 $v_{2}$ 에 인접한 정점 중 아직 탐색하지 않은 정점 $v_{3]$ 를 탐색하는 과정을 반복하여 그래프에 포함된 모든 정점을 탐색하는 방법
- 다음을 고려해서 그래프에 포함된 정점을 탐색한다.
| ① 어떤 정점 $v_{n}$ 에 인접한 정점이 여러 개인 경우, 탐색 기준에 따라 우선적으로 탐색하는 정점이 달라질 수 있다. 이 페이지에서는 가장 왼쪽에 있는 정점 또는 사전적 순서로 앞에 오는 정점부터 탐색한다. ② 어떤 정점 $v_{n}$ 에 인접한 모든 정점을 탐색하면 $v_{n}$ 에 인접하면서 $v_{n}$ 직전에 탐색한 정점 $v_{n - 1}$ 로 돌아가 $v_{n - 1}$ 에 인접하면서 탐색하지 않은 다른 정점 $v_{n + 1}$ 을 탐색한다. 이를 백트래킹(Backtracking)이라고 한다. |

예

- 위의 그래프에 대한 깊이 우선 탐색은 다음 과정으로 진행된다. 이 그래프에 대해서는 사전적 순서로 앞에 오는 정점부터 탐색한다.
| (1) 정점 `a` 에 인접하면서 아직 탐색하지 않은 정점 `b, c` 중 `b` 를 먼저 탐색 : `a - b` (2) 정점 `b` 에 인접하면서 아직 탐색하지 않은 정점 `d, e` 중 `d` 를 먼저 탐색 : `a - b - d` (3) 정점 `d` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `b` 로 백트래킹 (4) 정점 `b` 에 인접하면서 아직 탐색하지 않은 정점 `e` 를 탐색 : `a - b - d - e` (5) 정점 `e` 에 인접하면서 아직 탐색하지 않은 정점 `c, f` 중 `c` 를 먼저 탐색 : `a - b - d - e - c` (6) 정점 `c` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `e` 로 백트래킹 (7) 정점 `e` 에 인접하면서 아직 탐색하지 않은 정점 `f` 를 탐색 : `a - b - d - e - c - f` (8) 정점 `f` 에 인접하면서 아직 탐색하지 않은 정점 `g` 를 탐색 : `a - b - d - e - c - f - g` (9) 정점 `g` 에 인접하면서 아직 탐색하지 않은 정점 `h` 를 탐색 : `a - b - d - e - c - f - g - h` (10) 정점 `h` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `g` 로 백트래킹 (11) 정점 `g` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `f` 로 백트래킹 (12) 정점 `f` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `e` 로 백트래킹 (13) 정점 `e` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `b` 로 백트래킹 (14) 정점 `b` 에 인접하면서 아직 탐색하지 않은 정점이 없으므로 정점 `a` 로 백트래킹 (15) 정점 `a` 에 인접하면서 아직 탐색하지 않은 정점이 없고 시작 정점으로 돌아왔으므로 탐색 종료 |
- 위의 그래프를 깊이 우선 탐색하는 데 사용한 정점과 변을 정리하면 다음과 같은 신장 부분 그래프이다.

깊이 우선 탐색 과정
① 시작 정점 `v` 를 탐색한다.
② 정점 `v` 에 인접하는 정점 중 탐색하지 않은 정점 $v_{\text{sub}}$ 를 탐색한다.
③ 정점 $v_{\text{sub}}$ 를 정점 `v` 로 하여 ②를 반복한다.
④ 더 이상 탐색하지 않은 정점이 없으면 이전에 탐색한 정점을 `v` 로 하여 ②와 ③을 반복한다.
⑤ 그래프의 모든 정점을 탐색할 때까지 반복한다.
깊이 우선 탐색 알고리즘
DFS(V) {
탐색한 원소 리스트 S에 정점 v1을 추가;
탐색해야 할 원소 리스트 Vs에 V - {v1} 원소를 차례로 추가;
searched(v1);
}
searched(v) {
for (v에 인접한 vsub 가 vsub ∈ Vs) {
탐색한 원소 리스트 S에 정점 vsub를 추가;
탐색해야 할 원소 리스트 Vs에서 vsub를 제거;
searched(vsub);
}
}
너비 우선 탐색(BFS; Breadth First Search)
연결 그래프 $G = (V, \; E)$ 에 포함되는 어떤 정점 $v_{1}$ 을 시작 정점으로 할 때, $v_{1}$ 에 인접한 모든 정점을 탐색하고, 그 정점 중 하나인 $v_{2}$ 에 인접한 정점을 모두 탐색하는 방식을 반복하여 그래프에 포함된 모든 정점을 탐색하는 방법
- 위와 같은 방식으로 너비 우선 탐색을 하면 그래프의 시작 정점 $v_{1}$ 에 인접한 정점 $v_{2_{1}}, v_{2_{2}}, \cdots, v_{2_{n}}$ 을 모두 탐색한 후 우선 탐색할 정점을 선택하는 기준에 따라 선택된 정점 $v_{2_{1}}$ 에 인접한 정점 $v_{3_{1}}, v_{3_{2}}, \cdots, v_{3_{m}}$ 을 탐색한다.
- 그러므로 너비 우선 탐색 방식은 시작 정점에서 가까운 정점을 먼저 탐색하고 멀리있는 정점일수록 나중에 탐색한다.
- 이 과정에서 어떤 정점에 인접한 정점 중 우선 탐색할 정점을 선택하는 기준은 그래프의 목적에 따라 달라지는데, 이 페이지에서는 깊이 우선 탐색과 마찬가지로 가장 왼쪽에 있는 정점 또는 사전적 순서로 앞에 오는 정점부터 탐색한다.
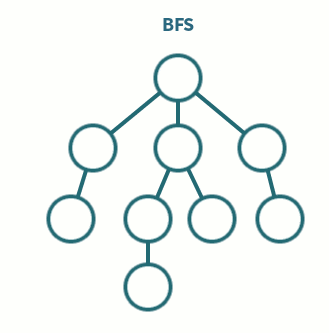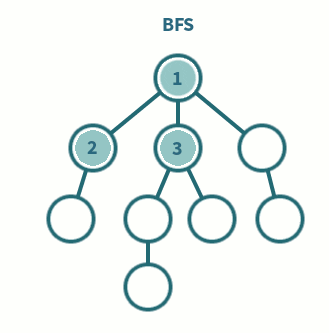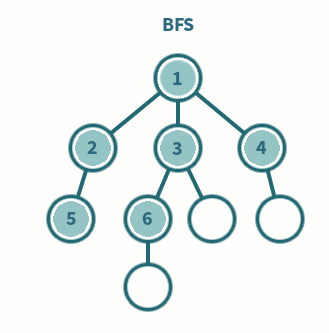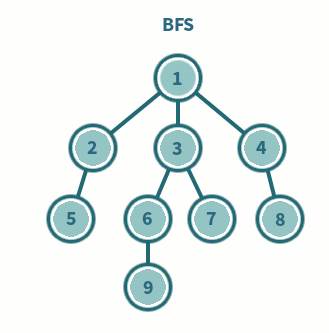
예

- 위의 그래프에 대한 너비 우선 탐색은 다음 과정으로 진행된다. 시작 정점은 `a` 로 하며, 사전적으로 앞에 오는 정점부터 탐색한다.
| (1) 정점 `a` 에 인접하면서 아직 탐색하지 않은 정점 `b, c` 중 `b` 를 탐색 : `a - b` (2) 정점 `a` 에 인접하면서 아직 탐색하지 않은 정점 `c` 를 탐색 : `a - b - c` (3) 탐색한 정점 `b, c` 중 먼저 탐색한 정점 `b` 에 인접하면서 아직 탐색하지 않은 정점 `d, e` 중 정점 `d` 를 탐색 : `a - b - c - d` (4) 정점 `b` 에 인접하면서 아직 탐색하지 않은 정점 `e` 를 탐색 : `a - b - c - d - e` (5) 탐색한 정점 `b, c` 중 나중에 탐색한 정점 `c` 에 인접하면서 아직 탐색하지 않은 정점은 없음. (6) 탐색한 정점 `d, e` 중 나중에 탐색한 정점 `d` 에 인접하면서 아직 탐색하지 않은 정점은 없음. (7) 탐색한 정점 `d, e` 중 나중에 탐색한 정점 `e` 에 인접하면서 아직 탐색하지 않은 정점 `f` 를 탐색 : `a - b - c - d - e - f` (8) 정점 `f` 에 인접하면서 아직 탐색하지 않은 정점 `g` 를 탐색 : `a - b - c - d - e - f - g` (9) 정점 `g` 에 인접하면서 아직 탐색하지 않은 정점 `h` 를 탐색 : `a - b - c - d - e - f - g - h` (10) 정점 `h` 에 인접하면서 아직 탐색하지 않은 정점이 없고, 더 이상 탐색할 정점이 없으므로 탐색 종료 |
- 위의 그래프를 너비 우선 탐색하는 데 사용한 정점과 변을 정리하면 다음과 같은 신장 부분 그래프이다.
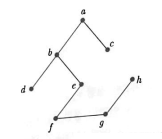
너비 우선 탐색 과정
① 시작 정점 `v` 를 탐색한다.
② 정점 `v` 에 인접하는 모든 정점 $v_{\text{sub}}$ 를 하나씩 탐색한다.
③ 정점 $v_{\text{sub}}$ 에 인접하는 모든 정점을 탐색한다.
④ 정점 $v_{\text{sub}}$ 를 정점 `v` 로 하여 모든 정점을 탐색할 때까지 ②, ③을 반복한다.
너비 우선 탐색 알고리즘
BFS(V) {
탐색한 원소 리스트 S에 정점 v1 추가;
탐색해야 할 원소 리스트 Vs에 v1에 인접하는 정점을 차례로 추가;
while (Vs에 탐색할 원소 존재) {
리스트 S에 정점 vsub ∈ Vs 를 추가;
for (vsub에 인접하는 정점 vx ∈ V) 존재 {
탐색해야 할 원소 리스트 Vs의 끝에 vx 추가;
}
탐색해야 할 원소 리스트 Vs에서 vsub 제거;
}
}
728x90
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 오일러와 해밀턴 (0) | 2022.11.26 |
|---|---|
| [이산 수학] 그래프의 표현 (0) | 2022.11.26 |
| [이산 수학] 그래프의 종류 (0) | 2022.11.25 |
| [이산 수학] 그래프의 개념 (0) | 2022.11.25 |
| [이산 수학] 함수의 종류 (0) | 2022.11.21 |
| [이산 수학] 합성 함수 (0) | 2022.11.21 |
| [이산 수학] 함수의 성질 (0) | 2022.11.14 |
| [이산 수학] 함수의 개념 (0) | 2022.11.14 |
