728x90
오일러와 해밀턴
- 연결 그래프에는 하나의 정점에서 다른 정점으로 가는 다양한 길이 존재할 수 있는데, 그 중에서 같은 변을 반복적으로 지나지 않는 길이 경로이다.
순환(Cycle) / 회로(Circuit)
연결 그래프에서 시작하는 정점과 끝나는 정점이 같은 경로
길이(Length)
경로 또는 순환을 구성하는 변의 수
- 한 그래프에 포함되는 임의의 정점에서 다른 정점 혹은 다시 원래의 정점으로 가는 길은 다양하다.
- 그중 변을 한 번씩만 지나 다른 정점으로 가는 길은 경로이고, 원래의 정점으로 다시 돌아오는 경로는 순환이다.
예
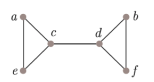 |
(1) $a - c - d - f$ (2) $a - e - c - d - b - f$ (3) $a - c - e - a$ (4) $a - e - c - a$ (5) $a - c - d - b - f - d - c - a$ |
- (1)부터 (5)는 모두 위의 그래프에서 가능한 길이다.
- 그 중, (1), (2)는 정점 `a` 에서 정점 `f` 까지의 길로 두 번 이상 중복되어 지나는 변이 없으므로 '정점 `a` 에서 정점 `f` 까지의 경로' 라고 구분한다.
- (3)과 (4)는 정점 `a` 에서 시작하여 정점 `a` 로 끝나는 길로, 두 번 이상 중복되어 지나는 변이 없고 시작한 정점 `a` 로 다시 돌아오는 길이므로 '정점 `a` 에서 시작하는 순환' 이라고 구분한다.
- (5)는 정점 `a` 에서 시작하여 정점 `a` 로 끝나는 길이지만, 변 `(c, d)` 가 두 번 반복되므로 경로도, 순환도 아닌 길이다.
- 경로인 `(1), (2)` 와 순환인 `(3), (4)` 는 길이를 구할 수 있는데 각각이 지나는 변의 수는 다음과 같다.
| (1) $a - c - d - f$ : $(a, c), (c, d), (d, f) \quad \Rightarrow \quad$ 변 3개 (2) $a - e - c - d - b - f$ : $(a, c), (e, c), (c, d), (d, b), (b, f) \quad \Rightarrow \quad$ 변 5개 (3) $a - c - e - a$ : $(a, c), (c, e), (e, a) \quad \Rightarrow \quad$ 변 3개 (4) $a - e - c - a$ : $(a, e), (e, c), (c, a) \quad \Rightarrow \quad$ 변 3개 |
- 그러므로 경로 (1)과 순환 (3), (4)의 길이는 3이고, 경로 (2)의 길이는 5이다.
- 네트워크의 신호 흐름이나 인공지능의 지식 연결, 하드웨어의 회로 등에서 신호나 지식의 흐름을 어떻게 구성하느냐는 시스템의 성능을 결정하는 주요한 기준 중 하나이다.
- 이러한 신호나 지식의 흐름을 계획하기 위해 그래프의 경로나 순환 개념을 응용할 수 있다.
- 그래프에서 경로나 순환을 찾는 대표적인 방법으로 수학자 레온하르트 오일러(Leonhard Euler)와 윌리엄 로언 해밀턴(William Rowan Hamilton)이 제안한 이론이 있다.
오일러 그래프(Eulerian Graph)
- 스위스 출신의 수학자 오일러는 각 지역을 연결하는 길을 한 번씩만 거쳐서 모든 지역을 돌아보고 원래 위치로 돌아오는 문제를 해결하기 위해 오일러 이론을 제안했다.
오일러 경로(Eulerian Path)
연결 그래프 $G = (V, \; E)$ 의 임의의 정점 `v` 에서 시작하여 모든 변을 꼭 한 번씩만 지나는 경로
오일러 순환(Eulerian Cycle) / 오일러 회로(Eulerian Circuit)
연결 그래프 $G = (V, \; E)$ 의 임의의 정점 `v` 에서 시작하여 모든 변을 꼭 한 번씩만 지나 다시 정점 `v` 로 돌아오는 경로
※ 오일러 그래프(Eulerian Graph) : 오일러 순환을 가지는 그래프
- 오일러 경로와 오일러 순환은 그래프에 포함된 모든 변을 반드시 한 번씩 지나야 한다.
- 그러므로 그래프에 따라 오일러 경로나 오일러 순환이 존재할 수도 있고 존재하지 않을 수도 있다.
예
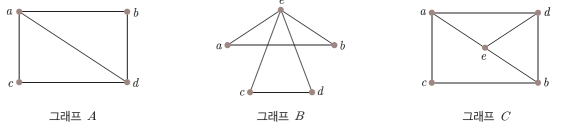
- 그래프 `A` 의 경우 오일러 경로는 있지만 오일러 순환은 없다. 그래프 `A` 에 포함된 오일러 경로는 다음과 같다.
| `a - b - d - c - a - d` | `a - b - d - a - c - d` | `a - c - d - b - a - d` |
| `a - c - d - a - b - d` | `a - d - b - a - c - d` | `a - d - c - a - b - d` |
| `d - a - b - d - c - a` | `d - a - c - d - b - a` | `d - b - a - c - d - a` |
| `d - b - a - d - c - a` | `d - c - a - b - d - a` | `d - c - a - d - b - a` |
- 이 경로들은 정점 `a` 나 정점 `d` 를 2번씩 지나지만, 그래프 `A` 를 구성하는 모든 변을 지나는 길이므로 오일러 경로이다.
- 오일러 경로에서는 정점 `a` 와 정점 `d` 가 경로의 시작점이거나 끝점이다.
- 정점 `c` 나 정점 `b` 를 시작점이나 끝점으로 하면 오일러 경로를 찾을 수 없다.
- 반면, 그래프 `A` 에서의 순환은 최소 1개의 변을 2번씩 지나야 하므로 오일러 순환은 존재하지 않는다.
- 그래프 `B` 의 경우에는 오일러 순환과 오일러 경로를 모두 찾을 수 있다.
- 그래프 `B` 의 정점 `a` 에서 시작하는 오일러 순환은 다음과 같다.
| `a - b - e - c - d - e - a` | `a - b - c - d - c - e - a` | `a - e - c - d - e - b - a` |
| `a - e - d - c - e - b - a` |
- 이 순환들은 그래프 `B` 의 정점 `e` 를 2번씩 지나지만, 모든 변을 한 번씩 지나므로 오일러 순환이다.
- 따라서 그래프 `B` 는 오일러 그래프이다.
- 위에서 찾은 그래프 `B` 에서의 오일러 순환은 곧 오일러 경로이기도 하다.
- 다만, 하나의 정점에서 시작하여 다시 자기 자신으로 돌아가는 오일러 경로(오일러 순환)만 존재하고, 다른 정점으로 가는 오일러 경로는 어떤 한 변을 지나지 않기 때문에 찾을 수 없다.
- 그래프 `C` 의 경우, 경로는 최소 하나의 변을 지나지 않고, 순환은 최소 2개의 변을 2번 지나므로 오일러 경로와 오일러 순환이 모두 존재하지 않는다.
- 주어진 그래프에 오일러 경로나 오일러 순환이 존재하는지를 판별하기 위해 정점의 차수를 활용할 수 있다.
오일러 그래프에 대한 정리
① 연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수인 것과 오일러 그래프는 서로 필요 충분 조건이다.
② 연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개인 것과 그래프에 오일러 경로가 존재하는 것은 서로 필요 충분 조건이다.
증명
① 증명 : 연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이다. $\Leftrightarrow$ 연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이다.
- (i) '연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이다.' ⇒ '연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이다.' 를 보이자.
- $|V| = 1$ 일 때, $v \in V$ 이고 $d(v) = 2m \; (m \in N)$ 이므로 정점 `v` 에 대한 루프가 `m` 개 존재하고, 정점 `v` 에서 시작하는 오일러 순환이 존재한다.
- ∴ $|V| = 1$ 일 때, 그래프 `G` 는 오일러 그래프이다.
- $|V| = k$ 일 때, `k` 개의 정점 모두의 차수가 $d(v_{i}) = 2n \; (n \in N, \; 1 \le i \le k)$ 이면 그래프 `G` 는 오일러 그래프라고 가정한다.
- $|V| = k + 1$ 일 때, 귀납 가정에서 오일러 그래프라고 가정한 $|V| = k$ 개이고, 각 정점의 차수가 $d(v_{i}) = 2n \; (n \in N, \; 1 \le i \le k)$ 인 그래프 `G` 를 편의상 $G_{1}$ 이라고 하자.
- 그래프 $G_{1}$ 에 $d(v) = 2m \; (m \in N)$ 인 정점 `v` 하나로 구성된 그래프 $G_{2}$ 를 연결할 때 각 정점의 차수는 $2p \; (p \in N)$ 이어야 하므로 두 그래프 $G_{1}$ 과 $G_{2}$ 사이에는 $2q \; (q \in N)$ 개의 변이 추가되어야 한다.
- 그러면 오일러 그래프 $G_{1}$ 과 그래프 $G_{2}$ 사이에 순환이 만들어진다.
- ∴ $|V| = k + 1$ 일 때, 그래프 `G` 는 오일러 그래프이다.
- ∴ 연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이면, 연결 그래프 $G = (V, \; E)$ 는 오일러 그래프이다.
- $|V| = 1$ 일 때, $v \in V$ 이고 $d(v) = 2m \; (m \in N)$ 이므로 정점 `v` 에 대한 루프가 `m` 개 존재하고, 정점 `v` 에서 시작하는 오일러 순환이 존재한다.
- (ii) '연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이다.' ⇒ '연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이다.' 를 보이자.
- 연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이므로 정점 $v \in V$ 에서 시작하여 정점 `v` 로 끝나는 오일러 순환이 존재하고, 이 때 $d(v) = 2m \; (m \in N)$ 이다.
- 또한 오일러 순환에 포함되는 각 정점은 정점으로 들어가는 변과 나오는 변을 갖게 되므로 각 정점의 차수는 짝수이다.
- ∴ 연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이면, 연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이다.
- 따라서 명제 "연결 그래프 $G = (V, \; E)$ 의 모든 정점의 차수가 짝수이다. $\Leftrightarrow$ 연결 그래프 $G = (V, \; E)$ 가 오일러 그래프이다." 는 참(T)이다.
② 증명 : 연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이다. $⇔$ 연결 그래프 $G = (V, \; E)$ 가 오일러 경로를 갖는다.
- (i) '연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이다.' ⇒ '연결 그래프 $G = (V, \; E)$ 가 오일러 경로를 갖는다.' 를 보이자.
- $V = \{v_{1}, v_{2}, \cdots, v_{k} \}$ 일 때 모든 정점의 차수가 $2m \; (m \in N)$ 인 경우, 즉 홀수 차수인 정점이 0개인 경우에는 오일러 순환이 존재하여 시작하는 정점에서 끝나는 경로가 만들어진다.
- 차수가 $2n \; (n \in N)$ 인 정점 $v_{1}$ 과 $v_{2}$ 를 연결하는 변 $(v_{1}, v_{2})$ 중 하나를 제거하면 두 정점의 차수는 `2n - 1` 로 홀수가 되므로 그래프 $G$ 에서 정점 $v_{1}$ 에서 시작하여 정점 $v_{2}$ 로 끝나거나, 정점 $v_{2}$ 에서 시작하여 정점 $v_{1}$ 으로 끝나는 경로가 만들어질 수 있다.
- ∴ 연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이면, 연결 그래프 $G = (V, \; E)$ 는 오일러 경로를 갖는다.
- (ii) '연결 그래프 $G = (V, \; E)$ 가 오일러 경로를 갖는다.' ⇒ 연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이다.' 를 보이자. '
- 그래프 `G` 가 오일러 경로를 가지므로 정점 $v_{1}$ 에서 시작하여 정점 $v_{2}$ 로 끝난다면 정점 $v_{1}$ 은 시작하는 변을, 정점 $v_{2}$ 는 끝나는 변을 각각 1개씩 기본적으로 가지므로, 두 정점 $v_{1}, v_{2}$ 의 차수는 모두 홀수이다.
- 그리고 두 정점 $v_{1}, v_{2}$ 를 제외한 나머지 정점은 하나의 변이 들어가고, 다른 하나의 변이 나와 변이 정점을 통과하는 형태이므로 차수가 짝수이다.
- 그러므로 차수가 홀수인 정점은 $v_{1}, v_{2}$ 2개 뿐이다.
- 또한, 그래프 `G` 가 오일러 경로를 가지므로 정점 $v_{i}$ 에서 시작하여 다시 정점 $v_{i}$ 로 끝나는 경로가 만들어질 수도 있다.
- 이 때, 정점 $v_{i}$ 에서 다른 정점으로 나가는 변과 다른 정점으로부터 들어오는 변, 이 2개의 변을 기본적으로 가지므로 정점 $v_{i}$ 의 차수는 짝수이다.
- 또한, 정점 $v_{i}$ 를 제외한 나머지 정점도 모두 들어가는 변과 나가는 변을 가져야 하므로 차수가 짝수이다.
- 따라서 그래프 `G` 를 구성하는 모든 정점의 차수는 짝수이므로 차수가 홀수인 정점은 0개이다.
- ∴ 연결 그래프 $G = (V, \; E)$ 가 오일러 경로를 가지면, 연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이다.
- 따라서 명제 "연결 그래프 $G = (V, \; E)$ 의 정점 중 차수가 홀수인 정점의 수가 0 또는 2개이다. $⇔$ 연결 그래프 $G = (V, \; E)$ 가 오일러 경로를 갖는다." 는 참(T)이다.
예

- 위의 세 그래프에 포함된 정점의 차수를 이용하여 오일러 경로나 오일러 순환이 존재하는지 다시 한번 확인해보자.
| 그래프 `A` : $d(a) = 3, \; d(b) = 2, \; d(c) = 2, \; d(d) = 3$ 그래프 `B` : $d(a) = 2, \; d(b) = 2, \; d(c) = 2, \; d(d) = 2, \; d(e) = 4$ 그래프 `C` : $d(a) = 3, \; d(b) = 3, \; d(c) = 2, \; d(d) = 3, \; d(e) = 3$ |
- 앞에서 오일러 경로를 구했던 그래프 `A` 에는 차수가 홀수인 정점이 2개 있고, 오일러 순환이 있어 오일러 그래프로 판단했던 그래프 `B` 는 짝수 차수인 정점만 포함한다.
- 오일러 경로도, 오일러 순환도 구할 수 없었던 그래프 `C` 의 경우 오일러 그래프에 대한 정리의 어느 경우에도 해당하지 않는다.
해밀턴 그래프(Hamiltonian Graph)
- 아일랜드 출신의 수학자 해밀턴은 그래프 이론을 이용해 어떤 길을 지나든 상관 없이 모든 지역을 반드시 한 번씩만 지나도록 하는 방법을 연구하였다.
- 다음 그림처럼 12면체 도형의 임의의 한 정점에서 시작하여 각 정점을 한 번씩 방문하고 시작했던 정점으로 돌아오는 방법을 찾는 것이었다.
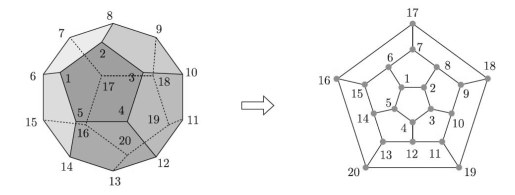
- 해밀턴은 이 연구에서 $17 - 16 - 15 - 14 - 5 - 1 - 6 - 7 - 8 - 2 - 3 - 4 - 12 - 13 - 20 - 19 - 11 - 10 - 9 - 17 - 17$ 이라는 순환을 찾아냈다.
해밀턴 경로(Hamiltonian Path)
연결 그래프 $G = (V, \; E)$ 의 모든 정점을 한 번씩만 지나는 경로
해밀턴 순환(Hamiltonian Cycle) / 해밀턴 회로(Hamiltonian Circuit)
연결 그래프 $G = (V, \; E)$ 의 임의의 정점 `v` 에서 시작하여 모든 정점을 딱 한 번씩만 지나 정점 `v` 로 다시 돌아오는 경로
※ 해밀턴 그래프(Hamiltonian Graph) : 해밀턴 순환을 갖는 그래프
- 오일러 경로, 오일러 순환과 다르게 해밀턴 경로, 해밀턴 순환은 같은 변을 몇 번 지나든, 혹은 지나지 않든 상관 없이 모든 정점을 반드시 한 번씩만 지나면 된다.
예
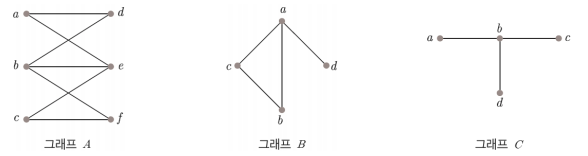
- 위 그림의 그래프 `A` 는 해밀턴 경로와 해밀턴 순환이 모두 존재하는 그래프이다.
- 정점 `a` 에서 시작하는 해밀턴 경로와 해밀턴 순환의 예는 다음과 같다.
| 해밀턴 경로 : `a - d - b - e - c - f` / `a - d - b - f - c - e` / `a - e - c -f - b - d` 해밀턴 순환 : `a - d - b - f - c - e - a` / `a - e - c - f - b - d - a` |
- 그래프 `A` 에 대한 해밀턴 경로나 순환에서 알 수 있듯이, 그래프를 구성하는 모든 변이 해밀턴 경로나 순환에 반드시 포함될 필요는 없다.
- 그러나 그래프를 구성하는 모든 정점은 해밀턴 경로나 순환에 반드시 한 번씩은 포함되어야 한다.
- 그래프 `B` 의 경우 다음과 같은 해밀턴 경로가 존재한다.
| `b - c - a - d` | `c - b - a - d` | `d - a - c - b` | `d - a - b - c` |
- 그러나 그래프 `B` 의 어떤 정점에서 시작하는 순환이든지 정점 `a` 를 2번은 지나야 하므로, 해밀턴 순환은 존재하지 않는다.
- 그래프 `C` 에 대한 어떤 경로나 순환이든 정점 `b` 를 2번 포함하므로 해밀턴 경로나 순환이 모두 존재하지 않는다.
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 그래프의 활용 (0) | 2022.11.27 |
|---|---|
| [이산 수학] 그래프의 표현 (0) | 2022.11.26 |
| [이산 수학] 그래프의 종류 (0) | 2022.11.25 |
| [이산 수학] 그래프의 개념 (0) | 2022.11.25 |
| [이산 수학] 함수의 종류 (0) | 2022.11.21 |
| [이산 수학] 합성 함수 (0) | 2022.11.21 |
| [이산 수학] 함수의 성질 (0) | 2022.11.14 |
| [이산 수학] 함수의 개념 (0) | 2022.11.14 |


