728x90
728x90
합성 함수
합성 함수의 정의
- 삼각 함수 공식 중 $\sin (α + β)$ 와 같은 식이 있다. 이 식은 다음과 같이 두 함수 `f(x)` 와 `g(x, y)` 를 합성한 결과이다.
$$f(x) = sin(x), \; g(x, y) = x + y \quad \Rightarrow \quad sin(α + β) = f(g(α, β))$$
- 이처럼 최초 입력을 이용해 2개 이상의 함수를 차례로 연산하여 최종 출력을 내어 입력과 출력을 대응하는 함수를 합성 함수라고 한다.
합성 함수(Composite Function : $g \circ f$ )
두 함수 $f : A \rightarrow B$ 와 $g : B \rightarrow C$ 가 있을 때, 집합 `A` 의 각 원소를 집합 `C` 의 원소에 대응하는 함수
$$g \circ f = (g \circ f)(x) = g(f(x)), \; x \in A$$
- 합성 관계와 마찬가지로 합성 함수를 구하려면 두 함수 사이에 공통으로 사용하는 집합이 있어야 한다.
- 공통으로 사용하는 집합은 한 함수에서는 정의역, 다른 함수에서는 공역으로 사용한다.
- 두 함수 $f : A \rightarrow B$ 와 $g : B \rightarrow C$ 가 있을 때, 집합 `B` 가 함수 `f` 에서는 공역, 함수 `g` 에서는 정의역으로 사용되므로 함수 `f` 와 `g` 는 합성할 수 있다.
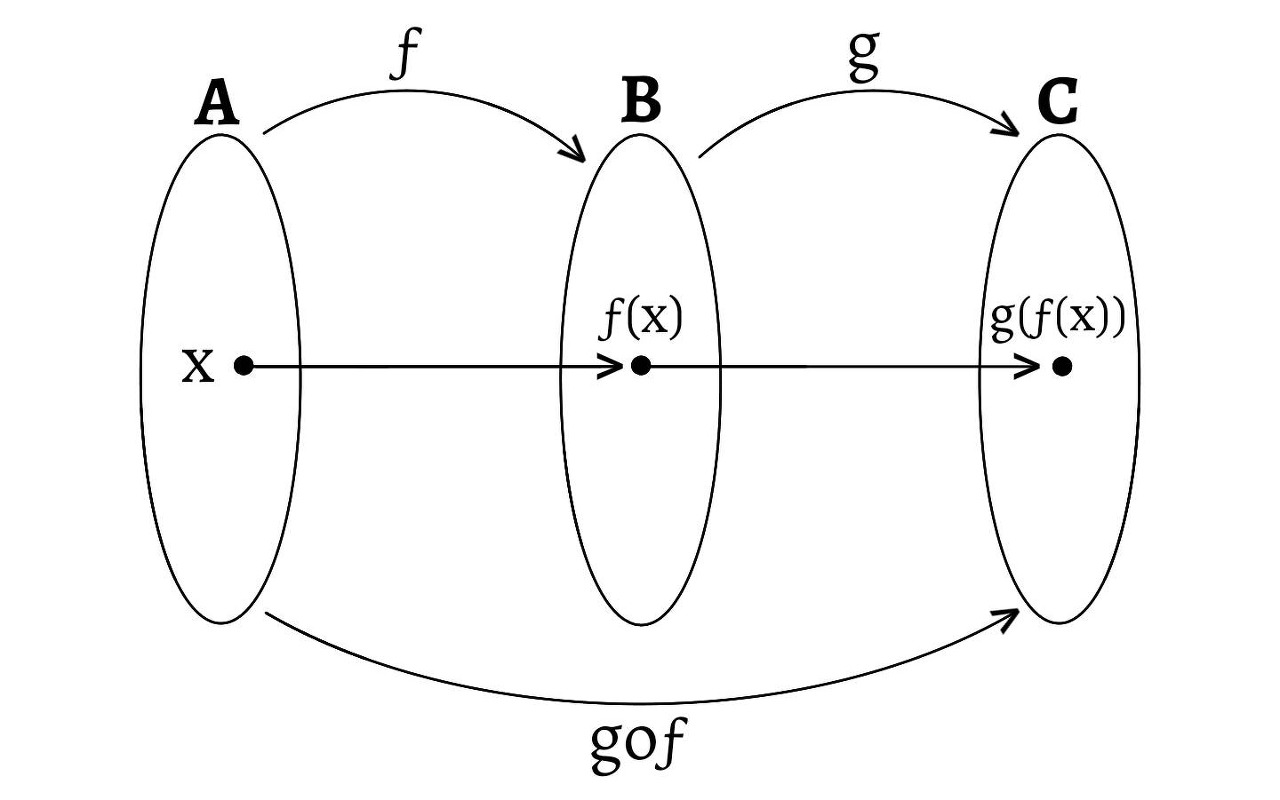
- 위의 그림의 두 함수 `f` 와 `g` 의 합성을 보면, 집합 `A` 의 원소 `x` 가 함수 `f` 에 의해 집합 `B` 의 원소 `f(x)` 와 대응하고, 집합 `B` 의 원소 `f(x)` 가 함수 `g` 에 의해 집합 `C` 의 원소 `g(f(x))` 와 대응한다.
- 그러므로 함수 `f` 다음 함수 `g` 순서로 연산하고, 나중에 연산하는 함수 `g` 를 앞에 위치하여 $g \circ f$ 로 표기한다.
- 또한, 합성 함수에서 최초로 입력하는 원소를 포함하는 집합이 정의역, 두 함수의 연산 결과인 원소를 포함하는 집합이 공역, 그리고 두 함수의 연산 결과인 원소들의 집합이 치역이다.
- 그러므로 위의 그림에서 합성 함수 $g \circ f$ 의 정의역은 집합 `A`, 공역은 집합 `C` 이고, 치역은 집합 `C` 의 부분 집합이다.
예
- 집합 $A = \{ 1, 2, 3, 4 \}, \; B = \{ a, b, c \}, \; C = \{ w, x, y, z \}$ 에 대한 다음 함수를 살펴보자.
| $$f : A \rightarrow B, \; f = \{(1, a), (2, b), (3, b), (4, c) \} \\ g : B \rightarrow C, \; g = \{(a, x), (b, w), (c, z) \} \\ h : C \rightarrow A, \; h = \{(w, 4), (x, 2), (y, 1), (z, 3) \} $$ |
- 이 함수 중 2개의 함수를 합성한다고 하면, 다음 3가지 합성 함수가 가능하다.
| $g \circ f = g(f(x)) \quad$ (∵ 함수 `f` 의 공역 `B` 가 함수 `g` 의 정의역이다.) $h \circ g = h(g(x)) \quad$ (∵ 함수 `g` 의 공역 `C` 가 함수 `h` 의 정의역이다.) $f \circ h = f(h(x)) \quad$ (∵ 함수 `h` 의 공역 `A` 가 함수 `f` 의 정의역이다.) |
- 그 외의 합성 함수 $f \circ g, \; g \circ h, \; h \circ f$ 는 정의역과 공역이 서로 일치하지 않으므로 구할 수 없다.
- $g \circ f$ 를 직접 구하면 다음과 같다.
 |
$g(f(1)) = g(a) = x$ $g(f(2)) = g(b) = w$ $g(f(3)) = g(b) = w$ $g(f(4)) = g(c) = z$ $∴ g \circ f = \{(1, x), (2, w), (3, w), (4, z) \}$ |
- 합성 함수 $g \circ f$ 의 정의역, 공역, 치역은 다음과 같다.
| $$\text{dom}(g \circ f) = A, \quad \text{codom}(g \circ f) = C, \quad \text{ran}(g \circ f) = \{ w, x, z \}$$ |
합성 함수와 교환 법칙
- 합성 함수의 교환 법칙은 성립하지 않는다. ($f \circ g \ne g \circ f$)
- 이것은 집합이 하나인 함수에 대해서도 동일하게 적용된다.
예
- 집합 $A = \{ 1, 2, 3 \}$ 에 대해 함수 $f : A \rightarrow A$ 와 $g : A \rightarrow A$ 가 다음과 같다고 할 때, 합성 함수 $g \circ f$ 와 $f \circ g$ 를 구하면 두 합성 함수의 결과는 전혀 다름을 알 수 있다.
| $$f : A \rightarrow A, \; f = \{(1, 3), (2, 1), (3, 2) \} \\ g : A \rightarrow A, \; g = \{(1, 1), (2, 3), (3, 3) \} \\ g \circ f = \{(1, 3), (2, 1), (3, 3) \} \\ f \circ g = \{(1, 3), (2, 2), (3, 2) \}$$ |
합성 함수와 결합 법칙
- 합성 함수의 결합 법칙은 성립한다.
예
- 집합 $A = \{ 1, 2, 3, 4 \}, \; B = \{ a, b, c, d, e \}, \; C = \{ x, y, z \}, \; D = \{ 11, 12, 13, 14 \}$ 에 대한 다음 함수를 살펴보자.
| $$f : A \rightarrow B, \; f = \{(1, c), (2, a), (3, c), (4, b) \} \\ g : B \rightarrow C, \; g = \{(a, x), (b, y), (c, y), (d, z), (e, z) \} \\ h : C \rightarrow D, \; h = \{(x, 12), (y, 11), (z, 14) \} $$ |
- 세 함수를 합성하여 합성 함수 $h \circ g \circ f$ 를 구하려고 한다.
- 이 합성 함수는 합성 함수의 정의에 의해 다음과 같이 합성 함수 $g \circ f$ 와 함수 `h` 를 합성할 수 있다.
| $$h \circ g \circ f = h(g(f(x))) = h \circ (g \circ f)$$ $h(g(f(1))) = h(g(c)) = h(y) = 11$ $h(g(f(2))) = h(g(a)) = h(x) = 12$ $h(g(f(3))) = h(g(e)) = h(z) = 14$ $h(g(f(4))) = h(g(b)) = h(y) = 11$ $∴ h \circ (g \circ f) = \{(1, 11), (2, 12), (3, 14), (4, 11) \}$ |
- 그러면 다음과 같이 합성 함수 $h \circ g$ 를 함수 `f` 와 합성한 결과는 어떨까?
| $$(h \circ g) \circ f = h(g(y)) \circ f = F \circ f$$ |
- 이 때, 간략한 표현을 위해 `h(g(y)) = F` 라고 하자.
- 우선 합성 함수 $h \circ g$ 를 구하면 다음과 같다.
| $h(g(a)) = h(x) = 12$ $h(g(b)) = h(y) = 11$ $h(g(c)) = h(y) = 11$ $h(g(d)) = h(z) = 14$ $h(g(e)) = h(z) = 14$ $∴ h \circ g = F = \{(a, 12), (b, 11), (c, 11), (d, 14), (e, 14) \}$ |
- 이 결과를 `f` 와 합성하여 $(h \circ g) \circ f = F \circ f$ 를 구하자.
| $F(f(1) = F(c) = 11$ $F(f(2) = F(a) = 12$ $F(f(3) = F(e) = 14$ $F(f(4) = F(b) = 11$ $∴ F \circ f = (h \circ g) \circ f = \{(1, 11), (2, 12), (3, 14), (4, 11) \}$ |
- 앞에서 구한 $h \circ (g \circ f)$ 의 결과와 $(h \circ g) \circ f$ 의 결과는 같다.
- 그러므로 합성 함수 $h \circ g \circ f$ 는 $h \circ (g \circ f)$ 로 구하든 $(h \circ g) \circ f$ 로 구하든 결과가 같으며, 이는 합성 함수의 결합 법칙이 성립함을 보여준다.
합성 함수의 성질
- 함수에 대해 단사 함수, 전사 함수, 전단사 함수와 같은 성질을 판별할 수 있듯이, 합성 함수도 성질을 판별할 수 있다.
- 합성 함수의 성질은 합성 함수를 구성하는 단일 함수의 성질에 따라 결정된다.
집합 `A, B, C` 에 대한 함수 $f : A \rightarrow B, \; g : B \rightarrow C$ 가 있을 때, 합성 함수 $g \circ f$ 의 성질은 다음과 같다.
① `f` 와 `g` 가 단사 함수이면, $g \circ f$ 도 단사 함수이다.
② `f` 와 `g` 가 전사 함수이면, $g \circ f$ 도 전사 함수이다.
③ `f` 와 `g` 가 전단사 함수이면, $g \circ f$ 도 전단사 함수이다.
④ $g \circ f$ 가 단사 함수이면, `f` 도 단사 함수이다.
⑤ $g \circ f$ 가 전사 함수이면, `g` 도 전사 함수이다.
⑥ $g \circ f$ 가 전단사 함수이면, `f` 는 단사 함수이고 `g` 는 전사 함수이다.
증명
- 합성 함수 $g \circ f : A \rightarrow C, \; g \circ f = g(f(x))$ 에서
① 증명
- `f` 가 단사 함수이므로 $a_{1}, a_{2} \in A$ 이고, $a_{1} \ne a_{2}$ 일 때 $f(a_{1}), f(a_{2}) \in B$ 이고 $f(a_{1}) \ne f(a_{2})$ 이다.
- 또한 함수 `g` 가 단사 함수이므로 $f(a_{1}), f(a_{2}) \in B$ 이고 $f(a_{1}) \ne f(a_{2})$ 일 때 $g(f(a_{1})), g(f(a_{2})) \in C$ 이고 $g(f(a_{1})) \ne g(f(a_{2}))$ 이다.
- ∴ $a_{1}, a_{2} \in A$ 이고 $a_{1} \ne a_{2}$ 일 때 $g(f(a_{1})), g(f(a_{2})) \in C$ 이고 $g(f(a_{1})) \ne g(f(a_{2}))$ 이다.
- ∴ `f` 와 `g` 가 단사 함수이면, $g \circ f$ 도 단사 함수이다.
② 증명
- `g` 가 전사 함수이므로 모든 원소 $c \in C$ 에 대해 $g(b) = c$ 를 만족하는 어떤 원소 $b \in B$ 가 존재한다.
- 또한 `f` 가 전사 함수이므로 모든 원소 $b \in B$ 에 대해 $f(a) = b$ 를 만족하는 어떤 원소 $a \in A$ 가 존재한다.
- ∴ $g(f(a)) = g(b) = c$ 로, 모든 원소 $c \in C$ 에 대해 $g(f(a)) = c$ 를 만족하는 어떤 원소 $a \in A$ 가 존재한다.
- ∴ `f` 와 `g` 가 전사 함수이면, $g \circ f$ 도 전사 함수이다.
③ 증명
- `f` 와 `g` 가 전단사 함수이면, 두 함수 모두 단사 함수이면서 전사 함수인 경우이므로 ①, ②에 의해 $g \circ f$ 는 단사 함수이면서 전사 함수이다.
- ∴ `f` 와 `g` 가 전단사 함수이면, $g \circ f$ 도 전단사 함수이다.
④ 증명
- $g \circ f$ 가 단사 함수이므로 $a_{1}, a_{2} \in A$ 이고, $a_{1} \ne a_{2}$ 일 때 $g(f(a_{1})), g(f(a_{2})) \in C$ 이고 $g(f(a_{1})) \ne g(f(a_{2}))$ 이다.
- 이 때, $g \circ f$ 가 단사 함수이므로 $g(f(a_{1})), g(f(a_{2})) \in C$ 이고 $g(f(a_{1})) \ne g(f(a_{2}))$ 이 성립하려면 $f(a_{1}), f(a_{2}) \in B$ 이고 $f(a_{1}) \ne f(a_{2})$ 이어야 한다.
- ∴ $a_{1}, a_{2} \in A$ 이고 $a_{1} \ne a_{2}$ 일 때 $f(a_{1}), f(a_{2}) \in B$ 이고 $f(a_{1}) \ne f(a_{2})$ 이다.
- ∴ $g \circ f$ 가 단사 함수이면 `f` 도 단사 함수이다.
⑤ 증명
- $g \circ f$ 가 전사 함수이므로 모든 원소 $c \in C$ 에 대해 $g(f(a)) = c$ 를 만족하는 어떤 원소 $a \in A$ 가 존재한다.
- 어떤 원소 $a \in A$ 가 존재하므로 이 `a` 에 대해 $f(a) = b$ 를 만족하는 어떤 원소 $b \in B$ 가 존재하고, $g(f(a)) = g(b) = c$ 임을 알 수 있다.
- ∴ 모든 원소 $c \in C$ 에 대해 $g(b) = c$ 를 만족하는 어떤 원소 $b \in B$ 가 존재한다.
- ∴ $g \circ f$ 가 전사 함수이면, `g` 도 전사 함수이다.
⑥ 증명
- $g \circ f$ 가 전단사 함수이면 $g \circ f$ 가 단사 함수이면서 전사 함수이므로, ④, ⑤에 의해 `f` 는 단사 함수이고 `g` 는 전사 함수이다.
- ∴ $g \circ f$ 가 전단사 함수이면, `f` 는 단사 함수이고 ` g` 는 전사 함수이다.
728x90
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 그래프의 표현 (0) | 2022.11.26 |
|---|---|
| [이산 수학] 그래프의 종류 (0) | 2022.11.25 |
| [이산 수학] 그래프의 개념 (0) | 2022.11.25 |
| [이산 수학] 함수의 종류 (0) | 2022.11.21 |
| [이산 수학] 함수의 성질 (0) | 2022.11.14 |
| [이산 수학] 함수의 개념 (0) | 2022.11.14 |
| [이산 수학] 동치 관계와 부분 순서 관계 (0) | 2022.11.06 |
| [이산 수학] 관계의 폐포 (0) | 2022.11.06 |

