728x90
합성 관계
- 2개 이상의 관계를 이용해 새로운 관계를 만드는 것을 '관계를 합성한다'고 하고, 이렇게 만든 관계를 합성 관계라고 한다.
합성 관계(Composite Relation : $S \circ R$)
집합 `A` 에서 집합 `B` 로의 관계 `R` 과 집합 `B` 에서 집합 `C` 로의 관계 `S` 가 있을 때, 이 두 관계를 이용해 구하는 집합 `A` 에서 집합 `C` 로의 관계
$$S \circ R = \{(a, c) ∈ A \times C \; | \; a ∈ A, \; b ∈ B, \; c ∈ C, \; (a, b) ∈ R, \; (b, c) ∈ S \}$$
- 합성 관계를 구하려면 둘 이상의 관계 사이에 공통으로 사용되는 자료 집합이 있어야 한다.
예
| 수강과목 담당교수 정보 | ||
| 학번 | 과목코드 | 교수번호 |
- 위의 '수강과목 담당교수 정보' 라는 관계는 아래의 '수강과목 정보'와 '담당과목 정보'라는 관계를 이용해 구할 수 있는데, 이 두 관계는 '과목코드' 라는 공통 자료 집합을 사용한다.
| 수강과목 정보 | 담당과목 정보 | |||
| 학번 | 과목코드 | 교수번호 | 과목코드 | |
- 이러한 공통 자료 집합이 두 관계를 연결하는 연결 고리 역할을 하여 합성 관계가 성립한다.
- 여기서 연결 고리인 자료 집합은 합성에 사용되는 두 관계 중 한 관계에서는 정의역이고, 다른 관계에서는 공역이어야 한다.
두 관계 사이의 합성이 가능한 경우

- (a)의 경우, 관계 `S` 의 정의역과 관계 `R` 의 공역이 집합 `B` 로 같으므로 합성 관계 $S \circ R$ 이 가능하다.
- $R → S$ 가 되므로 $S \circ R$ (합성할 때는 방향을 반대로 해준다.)
- 또한 (b)의 경우 관계 `R` 의 정의역과 관계 `S` 의 공역이 집합 `B` 로 같으므로 합성 관계 $R \circ S$ 가 가능하다.
- $S → R$ 이 되므로 $R \circ S$ (합성할 때는 방향을 반대로 해준다.)
두 관계 사이의 합성이 불가능한 경우

- 관계 `R` 과 `S` 중 어느 한 관계의 정의역과 다른 관계의 공역이 같아야 하는데 서로 다르므로 합성 관계 $S \circ R$ 과 $R \circ S$ 가 모두 불가능하다.
- 합성이 가능한 집합 `A` 에서 집합 `B` 로 가는 관계 `R` 과, 집합 `B` 에서 집합 `C` 로 가는 관계 `S` 를 합성할 때, 관계 `R` 의 공역이고 관계 `S` 의 정의역인 집합 `B` 가 두 관계의 연결 고리이므로 다음 그림처럼 합성할 수 있다.
- 이 합성의 결과는 집합 `A` 에서 집합 `C` 로 가는 관계이고, 합성 관계의 정의역은 집합 `A`, 공역은 집합 `C` 이다.
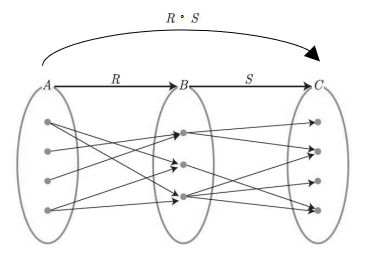
합성 관계의 표기
- 합성 관계는 표기에 주의해야 한다.
- 집합 `A` 에서 집합 `B` 로 가는 관계 `R` 과 집합 `B` 에서 집합 `C` 로 가는 관계 `S` 의 합성 관계는 $S \circ R$ 로 표기한다.
- 함수의 합성처럼 방향을 반대로 한다.
- 즉, 합성 관계를 표기할 때는 합성 관계의 정의역을 가지는 관계($R$)를 합성 연산자 $\circ$ 뒤에, 공역을 가지는 관계($S$)를 합성 연산자 $\circ$ 의 앞에 쓴다고 생각하고 표기한다.
- 집합 `A` 에서 집합 `B` 로 가는 관계 `R` 과 집합 `B` 에서 집합 `C` 로 가는 관계 `S` 의 합성 관계는 $S \circ R$ 로 표기한다.
예
- 집합 $A = \{ a, b, c, d \}, \; B = \{1, 2, 3 \}, \; C = \{ x, y, z \}$ 에 대한 관계 `R` 과 `S` 가 다음과 같다고 하자.
| $$R : A → B, \quad R = \{(a, 2), (b, 2), (b, 3), (c, 1), (d, 1), (d, 2), (d, 3) \} \\ S : B → C, \quad S = \{(1, x), (1, z), (2, y), (2, z), (3, x), (3, y) \}$$ |
- 집합 `B` 가 관계 `R` 에서는 공역으로, 관계 `S` 에서는 정의역으로 사용되므로 집합 `B` 를 연결 고리로 두 관계 `R` 과 `S` 를 합성할 수 있다.
- 두 관계 `R` 과 `S` 를 합성한 결과는 다음과 같다.
| $$S \circ R = \{(a, y), (a, z), (b, x), (b, y), (b, z), (c, x), (c, z), (d, x), (d, y), (d, z) \}$$ |
- 이 합성 관계의 정의역, 공역, 치역은 다음과 같다.
| $$\text{dom}(S \circ R) = A, \quad \text{codom}(S \circ R) = C, \quad \text{ran}(S \circ R) = \{ x, y, z \} = C$$ |
합성 관계와 교환 법칙
- 합성 관계는 교환 법칙이 성립하지 않는다.
- 집합 하나에 대한 관계이더라도 마찬가지이다.
예
- 집합 $A = \{ 1, 2, 3\}$ 에 대한 관계 `R` 과 `S` 가 다음과 같다고 가정한다.
| $$R : A → A, \quad R = \{(1, 1), (1, 3), (2, 3), (3, 1) \} \\ S : A → A, \quad S = \{(1, 1), (2, 1), (2, 2), (3, 2), (3, 3) \}$$ |
- 관계 `R` 과 `S` 를 합성하면 집합 `A` 가 두 관계에서 정의역이면서 공역이므로 다음과 같이 $R \circ S$ 와 $S \circ R$ 이 모두 가능하다.
| $$R \circ S = \{(1, 1), (1, 3), (2, 1), (2, 3), (3, 1), (3, 3) \} \\ S \circ R = \{(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 1) \}$$ |
- 위 결과를 보면 합성 관계는 교환 법칙이 성립하지 않음을 확인할 수 있다.
합성 관계의 거듭 제곱
합성 관계의 표현
- 합성 관계는 관계 행렬을 이용하여 구할 수 있는데, 이 때, 부울 행렬의 부울곱을 이용한다.
- 집합 `A`에서 집합 `B` 로 가는 관계 `R` 과 집합 `B` 에서 집합 `C` 로 가는 관계 `S` 의 합성은 관계 `R` 에 대한 관계 행렬 $M_{R}$ 과 관계 `S` 에 대한 관계 행렬 $M_{S}$ 의 부울곱으로 구한다.
- 관계 합성을 위해 부울곱 연산을 할 때, 관계 행렬의 순서는 부울곱 기호($\odot$)를 기준으로 합성 관계의 정의역을 갖는 관계 행렬이 앞에, 공역을 갖는 관계 행렬이 뒤에 위치한다.
- 즉, 다음과 같이 합성 관계 $S \circ R$ 을 구할 때 합성 관계 $S \circ R$ 의 정의역(집합 $A$)을 포함하는 관계 `R` 에 대한 관계 행렬이 부올곱의 앞에, 합성 관계의 공역(집합 $C$)을 포함하는 관계 `S` 에 대한 관계 행렬이 부올곱의 뒤에 위치한다.
$$S \circ R = M_{S \circ R} = M_{R} \odot M_{S}$$
예
- 집합 $A = \{ a, b, c, d \}, \; B = \{1, 2, 3 \}, \; C = \{ x, y, z \}$ 에 대한 관계 `R` 과 `S` 가 다음과 같다고 하자.
| $$R : A → B, \quad R = \{(a, 2), (b, 2), (b, 3), (c, 1), (d, 1), (d, 2), (d, 3) \} \\ S : B → C, \quad S = \{(1, x), (1, z), (2, y), (2, z), (3, x), (3, y) \}$$ |
- 합성 관계 $S \circ R$ 을 다음과 같이 부울 행렬의 부울곱으로 나타낼 수 있다.
| $$S \circ R = M_{S \circ R} = M_{R} \odot M_{S} \\ = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \end{bmatrix} \\ \quad \quad \begin{matrix} x & y & z \end{matrix} \\ = \begin{matrix} a \\ b \\ c \\ d \end{matrix} \begin{bmatrix} 0 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \end{bmatrix}$$ |
- 합성 관계 $S \circ R$ 의 행은 정의역 원소이고, 열은 공역 원소이므로 이에 따라 합성 관계를 순서쌍 집합으로 표현하면 다음과 같다.
| $$S \circ R = \{(a, y), (a, z), (b, x), (b, y), (b, z), (c, x), (c, z), (d, x), (d, y), (d, z) \}$$ |
합성 관계의 거듭 제곱 : $R^{n}$
집합 `A` 에 대한 관계 `R` 에 대하여 `n` 번의 합성으로 구하는 합성 관계
$$R^{n} = \begin{cases} R &, n = 1 \text{일 때} \\ R^{n-1} \circ R &, n > 1 \text{일 때}\end{cases}$$
- 일반적인 스칼라의 거듭 제곱처럼 하나의 집합에 대한 관계는 거듭해서 합성할 수 있는데, 이를 '합성 관계의 거듭 제곱'이라고 한다.
예
- 집합 $A = \{ 1, 2, 3 \}$ 에 대한 관계 `R` 의 관계 행렬이 $M_{R} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ 일 때 관계 $R^{2}, R^{3}, R^{4}$ 을 구해보자.
| $$R^{2} = R \circ R \Rightarrow M_{R} \odot M_{R} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}$$ |
- $R^{3}$ 의 경우, $R^{2}$ 을 이용하되, 거듭제곱식에서 $R^{2}$ 이 합성 연산자 $\circ$ 의 앞에 있어야 한다.
| $$R^{3} = R^{2} \circ R \Rightarrow M_{R} \odot M_{R^{2}} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix}$$ |
| $$R^{4} = R^{3} \circ R \Rightarrow M_{R} \odot M_{R^{3}} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}$$ |
추이 관계와 거듭 제곱의 관계
집합 `A` 에 대한 관계 `R` 이 추이 관계일 때, 필요 충분 조건은 모든 양의 정수 `n` 에 대하여 $R^{n} ⊆ R$ 인 것이다.
증명
- 다음 두 조건 명제가 모두 참(T)임을 증명한다.
| (i) 집합 `A` 에 대한 관계 `R` 이 추이 관계이면, 모든 양의 정수 `n` 에 대하여 $R^{n} ⊆ R$ 이다. (ii) 모든 양의 정수 `n` 에 대하여 $R^{n} ⊆ R$ 이면, 집합 `A` 에 대한 관계 `R` 이 추이 관계이다. |
(i) 증명
- 기본 가정
- `n = 1` 일 때, 집합 `A` 에 대한 관계 `R` 이 추이 관계이면 $R^{1} ⊆ R$ 이다.
- 귀납 가정
- `n = k` 일 때, 집합 `A` 에 대한 관계 `R` 이 추이 관계이면 $R^{k} ⊆ R$ 이다.
- 귀납 증명
- `n = k + 1` 일 때, 집합 `A` 에 대한 관계 `R` 이 추이 관계이면 $R^{k + 1} ⊆ R$ 임을 증명한다.
- $(a, c) ∈ R^{k+1}$ 이면 $(a, c) ∈ R^{k} \circ R$ 이다.
- ∵ $R^{k+1} = R^{k} \circ R$
- 그러면 $(a, b) ∈ R$ 이고 $(b, c) ∈ R^{k}$ 를 만족하는 $y ∈ A$ 가 존재한다.
- 귀납 가정에서 $R^{k} ⊆ R$ 이 성립한다고 가정했으므로 $(b, c) ∈ R$ 이다.
- $(a, b) ∈ R, \; (b, c) ∈ R$ 이고 `R` 이 추이 관계이므로 $(a, c) ∈ R$ 이다.
- 즉, $(a, c) ∈ R^{k + 1}$ 이면, $(a, c) ∈ R$ 이므로 $R^{k + 1} ⊆ R$ 이 성립한다.
- ∴ 조건 명제 (i)은 참(T)이다.
(ii) 증명
- 모든 양의 정수 `n` 에 대하여 $R^{n} ⊆ R$ 이므로, $R^{2} ⊆ R$ 이 성립한다.
- $(a, b) ∈ R, \; (b, c) ∈ R$ 이라고 가정하면, 합성의 정의에 따라 $(a, c) ∈ R^{2}$ 이다.
- ∵ $R^{2} = R \circ R$
- 이 때, $R^{2} ⊆ R$ 이므로 $(a, c) ∈ R$ 이다.
- 따라서 $(a, b) ∈ R, \; (b, c) ∈ R$ 이면 $(a, c) ∈ R$ 이므로 $R^{k + 1} ⊆ R$ 이 성립한다.
- ∴ 조건 명제 (ii)는 참(T)이다.
- 합성 관계의 거듭 제곱을 이용하여 어떤 관계의 추이 관계에 대한 여부를 판별할 수 있다.
- 원소가 `n` 개인 집합 `A` 에 대한 관계 `R` 을 `n` 번 합성한 결과가 관계 `R` 의 부분 집합이면 추이 관계로 판별할 수 있다.
예
- 집합 $A = \{ 1, 2, 3\}$ 에 대한 다음 관계 `R` 과 `S` 가 추이 관계인지 판별해보자.
| $$M_{R} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad M_{S} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ |
- `A` 집합의 원소는 3개이므로 관계 `R` 과 `S` 를 각각 3번씩 합성한다.
- 관계 $R^{3}$ 에 대한 거듭 제곱 $R^{3}$ 은 다음과 같다.
| $$R^{3} = R^{2} \circ R \Rightarrow M_{R} \odot M_{R^{2}} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix}$$ |
- 관계 `S` 에 대한 거듭제곱을 구하면 다음과 같다.
| $$S^{2} = S \circ S \Rightarrow M_{S} \odot M_{S} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ |
| $$S^{3} = S^{2} \circ S \Rightarrow M_{S} \odot M_{S^{2}} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \odot \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ |
- 이렇게 구한 관계 $R^{3}$ 과 $S^{3}$ 는 각각 다음과 같다.
| $$R^{3} = \{(1, 2), (1, 3), (2, 1), (2, 3), (3, 3) \} \\ S^{3} = \{(1, 1), (1, 2), (2, 1), (2, 2), (3, 1) \}$$ |
- 이 결과에 따라 관계 `R^{3}` 은 `R` 의 부분 집합이 아니고($R^{3} \not ⊆ R$), 관계 `S^{3}` 은 `S` 의 부분 집합($S^{3} ⊆ S$)임을 알 수 있다.
- 관계 `R` 처럼 합성 관계 `R^{3}` 이 `R` 의 부분 집합이 되지 않는 경우, 관계 `R` 은 추이 관계가 아니라고 할 수 있다.
- 반면, 관계 `S` 처럼 합성 관계 `S^{3}` 이 `S` 의 부분 집합인 경우, 관계 `S` 는 추이 관계라고 할 수 있다.
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 함수의 성질 (0) | 2022.11.14 |
|---|---|
| [이산 수학] 함수의 개념 (0) | 2022.11.14 |
| [이산 수학] 동치 관계와 부분 순서 관계 (0) | 2022.11.06 |
| [이산 수학] 관계의 폐포 (0) | 2022.11.06 |
| [이산 수학] 관계의 성질 (0) | 2022.10.31 |
| [이산 수학] 관계의 표현 (0) | 2022.10.29 |
| [이산 수학] 관계의 개념 (0) | 2022.10.29 |
| [이산 수학] 집합의 분할 (0) | 2022.10.22 |


