◀️ 🌱 November 🌱 ▶️
일	월	화	수	목	금	토
						0
0	0	0	0	0	0	0
0	0	0	0	0	0	0
0	0	0	0	0	0	0
0	0	0	0	0	0	0
0

[이산 수학] 조건 명제

2022. 10. 2. 21:05

728x90

조건 명제

앞 글에서 합성 명제를 구성하는 단순 명제에 대해 어떤 역할을 부여하지 않았다.
그러나 단순 명제에 역할을 부여해 그 단순 명제의 역할이 무엇이냐에 따라 진릿값이 결정되는 합성 명제가 있는데, 조건 명제가 이에 해당한다.

조건 명제(Conditional Proposition : $p → q$ ) / 함축(Implication)

명제 $p, q$ $p, q$ 에 대하여, 명제 $p$ $p$ 가 전제(Premise) 또는 가정(Hypothesis)이고 명제 $q$ $q$ 가 결론(Conclusion) 또는 결과(Consequence)인 명제

'지구의 자전축이 기울어져 있다면, 지구의 계절은 바뀐다'는 '지구의 자전축이 기울어져 있다( $p$ )'와 $지 구 의 계 절 은 바 뀐 다 . ($ q`)' 라는 두 명제를 결합한 합성 명제이다.
- $p$ $p$ : 전제
- $q$ $q$ : 결론
이처럼 전제와 결론의 관계로 결합된 합성 명제를 조건 명제라고 한다.
조건 명제 $p \to q$ $p → q$ 를 표현하는 문장은 다음과 같다.

- $p$ $p$ 이면 $q$ $q$ 이다. (if $p$ $p$ , then $q$ $q$ )
- $p$ $p$ 는 $q$ $q$ 를 함축한다. ( $p$ $p$ implies $q$ $q$ )
- $q$ $q$ 일 경우에만 $p$ $p$ 이다. ( $p$ $p$ only if $q$ $q$ )
- $p$ $p$ 는 $q$ $q$ 이기 위해 충분하다. ( $p$ $p$ is sufficient for $q$ $q$ )
- $q$ $q$ 는 $p$ $p$ 를 위해 필요하다. ( $q$ $q$ is necessary for $p$ $p$ )

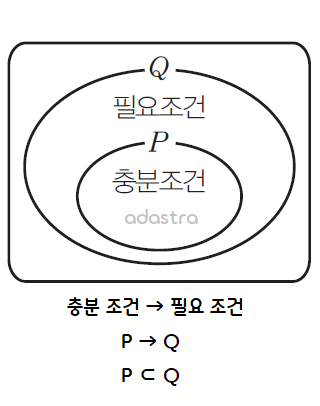
조건 명제의 진리표

$p$ $p$	$q$ $q$	$p \to q$ $p → q$
T	T	T
T	F	F
F	T	T
F	F	T

조건 명제 $p \to q$ $p → q$ 는 전제 명제 $p$ $p$ 가 참(T)이고 결론 명제 $q$ $q$ 가 거짓(F)인 경우에만 거짓(F)이고, 그 외의 경우에는 모두 참(T)이다.

예제 : 조건 명제

'양궁 과녁의 정 가운데를 맞추면 점수는 10점이다.' 라는 조건 명제가 있다고 하자.
- '양궁 과녁의 정 가운데를 맞춘다' : 명제 $p$ $p$ (전제)
- '점수는 10점이다.' : 명제 $q$ $q$ (결론)
이 전제와 결론을 이용하여 각 경우에 따른 조건 명제의 진릿값을 판별해보면 다음과 같다.

경우	설명	$p \to q$ $p → q$
1	양궁 과녁의 정 가운데를 맞춰서( $p$ $p$ 가 T), 점수가 10점( $q$ $q$ 가 T)이면 확실히 참(T) 상태이다.	참(T)
2	양궁 과녁의 정 가운데를 맞추지 않아도( $p$ $p$ 가 F), 점수가 10점( $q$ $q$ 가 T)인 경우는 과녁의 정 가운데가 아니더라도 가장 작은 원 안에만 맞추면 10점이므로 참(T)이다.	참(T)
3	양궁 과녁의 정 가운데를 맞추지 않는 경우( $p$ $p$ 가 F) 중, 점수가 10점이 아닌 경우( $q$ $q$ 가 F)는 과녁에서 9점 이하인 영역을 맞추는 경우가 있으므로 참(T)이다.	참(T)
4	양궁 과녁의 정 가운데를 맞췄는데도( $p$ $p$ 가 T) 점수가 10점이 아닌 경우( $q$ $q$ 가 F)는 있을 수 없으므로 거짓(F)이다.	거짓(F)

그러므로 전제에 해당하는 명제가 참(T)일 때, 결론에 해당하는 명제가 거짓(F)인 경우를 제외한 모든 경우에 조건 명제의 진릿값은 참(T)이다.

조건 명제는 어떤 사실을 증명하거나 추론할 때 유용하게 쓰인다. 이를 위해 조건 명제를 역, 이, 대우와 같은 형태의 명제로 변형할 수 있다.

명제 $p$ $p$	지구의 자전축은 기울어져 있다.
명제 $q$ $q$	지구의 계절이 바뀐다.
조건 명제 $p \to q$ $p → q$	지구의 자전축이 기울어져 있다면, 지구의 계절은 바뀐다.

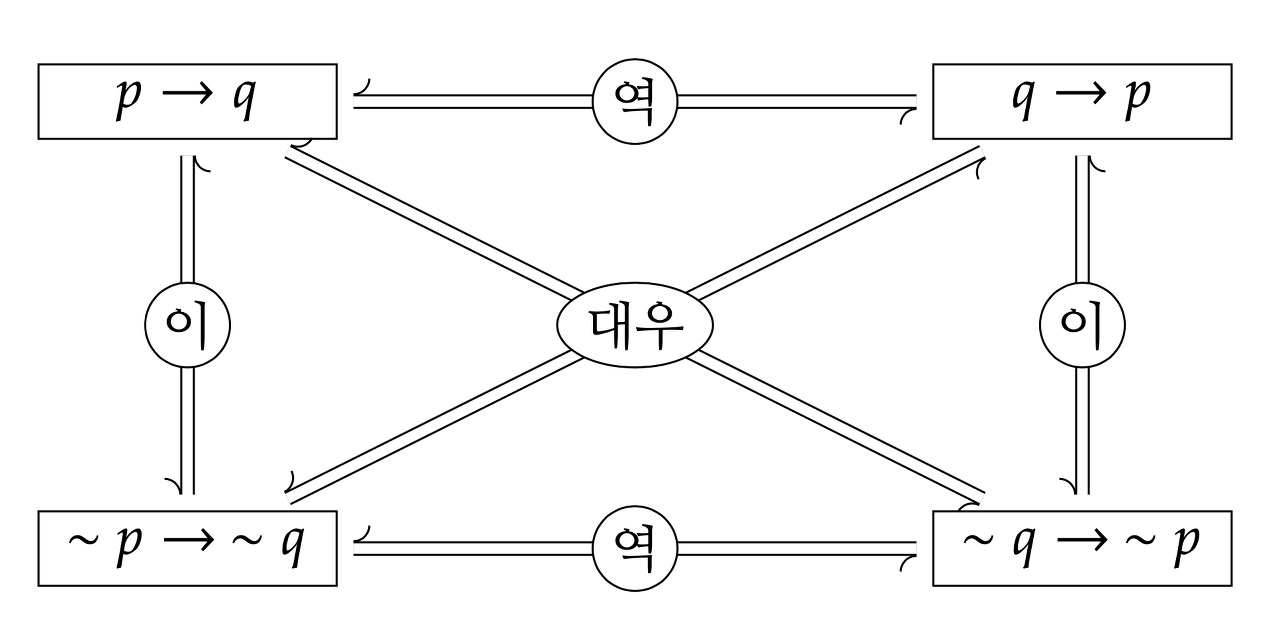
역(Converse)

조건 명제 $p \to q$ $p → q$ 에 대하여, $q \to p$ $q → p$ 형태의 명제

조건 명제 $p \to q$ $p → q$ 에서 전제 명제 $p$ $p$ 가 결론이 되고, 결론 명제 $q$ $q$ 가 전제가 되는 명제
$p \to q$ $p → q$ 의 역 $q \to p$ $q → p$ 는 다음과 같다.

q \to p

$q → p$

지구의 계절이 바뀌면, 지구의 자전축이 기울어져 있다.

이(Inverse)

조건 명제 $p → q$ 에 대하여, $\neg p → \neg q$ 형태의 명제

조건 명제 $p \to q$ $p → q$ 에서 명제 $p$ 의 부정 $\neg p$ 를 전제로, 명제 $q$ 의 부정 $\neg q$ 를 결론으로 하는 명제
$p \to q$ $p → q$ 에 대한 이 $\neg p → \neg q$ 는 다음과 같다.

\neg p \to \neg q

$\neg p → \neg q$

지구의 자전축이 기울어져 있지 않다면, 지구의 계절은 바뀌지 않는다.

대우(Contraposition)

조건 명제 $p → q$ 에 대하여, $\neg q → \neg p$ 형태의 명제

조건 명제 $p \to q$ $p → q$ 에서 명제 $p$ 의 부정 $\neg p$ 가 결론이 되고, 명제 $q$ 의 부정 $\neg q$ 가 전제가 되는 명제
$p \to q$ $p → q$ 에 대한 대우 $\neg q → \neg p$ 는 다음과 같다.

\neg q \to \neg p

$\neg q → \neg p$

지구의 계절이 바뀌지 않으면, 지구의 자전축이 기울어져 있지 않다.

역, 이, 대우의 진리표

$p$ $p$	$q$ $q$	조건 명제	역	이	대우
$p$ $p$	$q$ $q$	$p \to q$ $p → q$	$q \to p$ $q → p$	$\neg p → \neg q$	$\neg q → \neg p$
T	T	T	T	T	T
T	F	F	T	T	F
F	T	T	F	F	T
F	F	T	T	T	T

본 명제와 대우 명제의 진릿값은 같다.
- 본 명제를 이용하여 증명 또는 추론하기 어려운 경우에는 대우 명제로 바꿔서 할 수 있다.

쌍방 조건 명제(Biconditional Proposition : $p ↔ q$ )

명제 $p, q$ $p, q$ 가 모두 전제이면서 동시에 결론인 명제

하나의 명제가 전제이면서 결론일 수 있는 합성 명제를 쌍방 조건 명제라고 한다.
쌍방 조건 명제 $p \leftrightarrow q$ $p ↔ q$ 는 다음과 같이 표현한다.

- $p$ $p$ 이면 $q$ $q$ 이며, 그 반대도 성립한다. (if $p$ $p$ then $q$ $q$ , and conversely)
- $p$ $p$ 는 $q$ $q$ 의 필요 충분 조건이다. ( $p$ $p$ is necessary and sufficient for $q$ $q$ )

쌍방 조건 명제의 진리표

$p$ $p$	$q$ $q$	$p \leftrightarrow q$ $p ↔ q$
T	T	T
T	F	F
F	T	F
F	F	T

$p ↔ q ≡ (p → q) \land (q → p)$

쌍방 조건 명제는 다음과 같은 두 명제의 논리곱(AND)으로 표현할 수 있다.
- $(p \to q)$
  - 단순 명제 $p$ $p$ : 전제
  - 단순 명제 $q$ $q$ : 결론
- $(q \to p)$
  - 단순 명제 $q$ $q$ : 전제
  - 단순 명제 $p$ $p$ : 결론

$$p ↔ q ≡ (p → q) \land (q → p)$$

증명 진리표

$p$	$q$	$p ↔ q$	$p → q$	$q → p$	$(p → q) \land (q → p)$
T	T	T	T	T	T
T	F	F	F	T	F
F	T	F	T	F	F
F	F	T	T	T	T

728x90

저작자표시 비영리 변경금지 (새창열림)

'Mathematics > 이산 수학' 카테고리의 다른 글

[이산 수학] 추론 (1)	2022.10.08
[이산 수학] 명제 함수와 한정자 (0)	2022.10.07
[이산 수학] 논리적 동치 (1)	2022.10.03
[이산 수학] 합성 명제 (0)	2022.10.02
[이산 수학] 논리 연산자 (0)	2022.10.02
[이산 수학] 명제 (0)	2022.10.02
[이산 수학] 컴퓨터에서의 수의 표현과 연산 (0)	2022.09.27
[이산 수학] 진법별 사칙연산 (0)	2022.09.26

Per ardua ad astra."Hello, World!" 🤖

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Per ardua ad astra.

"Hello,

[이산 수학] 조건 명제

조건 명제

조건 명제(Conditional Proposition : $p → q$ ) / 함축(Implication)

역(Converse)

이(Inverse)

대우(Contraposition)

쌍방 조건 명제(Biconditional Proposition : $p ↔ q$ )

$p ↔ q ≡ (p → q) \land (q → p)$

증명 진리표

'Mathematics > 이산 수학' 카테고리의 다른 글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역

Per ardua ad astra.

"Hello,

[이산 수학] 조건 명제

조건 명제

조건 명제(Conditional Proposition : p→qp→qp → q) / 함축(Implication)

역(Converse)

이(Inverse)

대우(Contraposition)

쌍방 조건 명제(Biconditional Proposition : p↔qp↔qp ↔ q)

p↔q≡(p→q)∧(q→p)p↔q≡(p→q)∧(q→p)p ↔ q ≡ (p → q) \land (q → p)

증명 진리표

'Mathematics > 이산 수학' 카테고리의 다른 글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역

조건 명제(Conditional Proposition : $p → q$ ) / 함축(Implication)

쌍방 조건 명제(Biconditional Proposition : $p ↔ q$ )

$p ↔ q ≡ (p → q) \land (q → p)$