[Algorithm] 이항 계수(Binomial Coefficient)

이항 계수(Binomial Coefficient)

개념

• 이항식을 이항 정리로 전개했을 때 각 항의 계수(Coefficient)
• 주어진 크기의 (순서 없는) 조합의 가짓수(${}_{n}C_{k}$)
• 파스칼의 삼각형의 형태로 이미 중세 동서양 수학에 알려져 있었다.
• 오늘날 쓰이는 표기법  $\displaystyle { n \choose k }$ 은 안드레아스 프라이헤르 폰 에팅스하우젠(Andreas Freiherr von Ettingshausen)이 1826년에 도입하였다.

 

정의

• 자연수 `n` 및 정수 `k` 가 주어졌을 때, $\displaystyle { n \choose k }$ 는 다음과 같다.

$${n \choose k} = \begin{cases} {}_{n}C_{k} = \frac{n!}{k!(n - k)!} & 0 \le k \le n \\ 0 & k < 0 \\ 0 & k > n \end{cases}$$

• 이항 계수를 $\displaystyle { n \choose k }$ 대신 $_{n}C_{k}$ 나 $C(n, \; k)$ 로 쓰기도 한다.
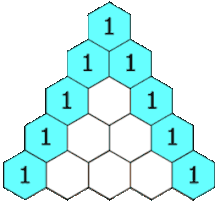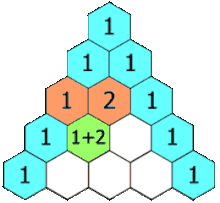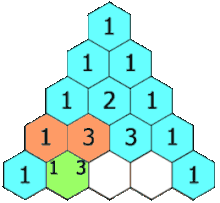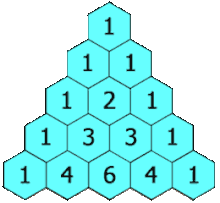
• 이항 계수의 값을 삼각형 모양으로 나열한 표를 파스칼의 삼각형(Pascal's Triangle)이라고 한다.

파스칼의 삼각형, 파스칼의 삼각형 속의 숫자들은 바로 윗 줄에 인접하는 두 숫자의 합으로 정의된다.

• `n = 2k` 인 경우의 이항 계수를 중심 이항 계수(Central Binomial Coefficient)라고 한다.
  • $k = 0, 1, 2, \cdots$ 일 때, 중심 이항 계수는 $1, 2, 6, 20, 70, 252, 924, 432, 12870, 48620, \cdots$ 이다.

 

성질

항등식

• 이항 계수는 다음과 같은 항등식을 만족시킨다.
  • 이는 이항 계수의 정의로부터 쉽게 증명할 수 있다.

$${n \choose k} = {n \choose n - k}$$

• 다음과 같은 점화식이 성립하며, 이는 파스칼의 법칙(Pascal's Rule)이라고 한다.

$${n \choose k} + {n \choose k + 1} = {n + 1 \choose k + 1}$$

 

응용

조합론

• 조합론에서 이항 계수는 크기가 `n` 인 유한 집합의 크기가 `k` 인 부분 집합의 수이다.
  • `n` 개의 원소와 `k` 개의 조합의 수

 

알고리즘

반복 알고리즘

• 이항 계수의 다음과 같은 항등식을 이용한다.

$${n \choose k} = {n \choose n - k}$$

#include <iostream>
using namespace std;

int factorial(int n) {
    int result = 1;
    for (int i = n; n > 0; n--) {
        result *= n;
    }
    return result;
}

int main() {
    int n, k, result;
    
    // 5C2 구해보기
    n = 5;
    k = 2;
    
    result = factorial(n) / (factorial(k) * factorial(n - k));
    
    cout << n << "C" << k << " = " << result << endl;
    
    return 0;
}

5C2 = 10

 

• 다음과 같이 팩토리얼 계산을 최소화하여 효율적으로 연산이 가능하도록 코드를 작성할 수 있다.
  • 예) ${}_{7}C_{5}$ 를 구할 경우
    • 이항 계수의 성질을 이용하여 $_{7}C_{2}$ 를 구한다.
    • $_{7}C_{2} = \frac{7!}{2! \times 5!}$ 을 계산하는 대신 $\frac{7 \times 6}{2!}$ 을 계산한다. 

#include <iostream>
using namespace std;

int factorial(int n) {
    int result = 1;
    for (int i = n; n > 0; n--) {
        result *= n;
    }
    return result;
}


int nCk(int n, int k) {
    if (k == 0 || k == n) return 1;
    else if ((0 < k) && (k < n)) {
        int numerator = 1;
        if (k > n / 2) k = n - k;
        for (int i = 1; i <= k; i++, n--) {
            numerator *= n;
        }
        return numerator / factorial(k);    
    }
    else return 0;
}

int main() {
    int n, k, result;
    
    // 7C5 구해보기
    n = 7;
    k = 5;
    
    result = nCk(n, k);
    
    cout << n << "C" << k << " = " << result << endl;
    
    return 0;
}

7C5 = 21

 

순환 알고리즘

• 이항 계수의 다음과 같은 항등식을 이용한다.

$${n \choose k} + {n \choose k + 1} = {n + 1 \choose k + 1}$$

$C(n, \; k) = C(n - 1, \; k - 1) + C(n - 1, \; k) \\ C(n, \; 0) = C(n, \; n) = 1$

 

• 순환 알고리즘을 사용하기 때문에 동일한 계산을 반복하는 단점이 존재한다.

#include <iostream>
using namespace std;

int nCk(int n, int k) {
    if (k == 0 || k == n) return 1;
    else if ((0 < k) && (k < n)) return nCk(n - 1, k - 1) + nCk(n - 1, k);
    else return 0;
}

int main() {
    int n, k, result;
    
    // 7C5 구해보기
    n = 7;
    k = 5;
    
    result = nCk(n, k);
    
    cout << n << "C" << k << " = " << result << endl;
    
    return 0;
}

7C5 = 21

 

• 혹은 다음과 같이 알고리즘을 작성해도 된다.

int nCk(int n, int k) {
    if (k > n) {
        return 0;
    }
    if (k == 0 || k == n) {
        return 1;
    }
    return nCk(n - 1, k - 1) + nCk(n - 1, k);
}

 

동적 계획법(DP)

• 메모이제이션(Memoization)을 활용하여 다음과 같이 코드를 작성할 수 있다.

#include <iostream>
using namespace std;

int dp[100][100];
int nCk(int n, int k) {
    if (dp[n][k] > 0) {
        return dp[n][k];
    }
    else if (k == 0 || k == n) {
        return dp[n][k] = 1;
    }
    else if ((0 < k) && (k < n)) {
        return dp[n][k] = nCk(n - 1, k - 1) + nCk(n - 1, k);
    }
    else {
        return 0;
    }
}

int main() {
    int n, k, result;
    
    // 7C5 구해보기
    n = 7;
    k = 5;
    
    result = nCk(n, k);
    
    cout << n << "C" << k << " = " << result << endl;
    
    return 0;
}

7C5 = 21

 

관련 문제

• https://dev-astra.tistory.com/277

[BOJ-11050][C++] 이항 계수 1

• https://dev-astra.tistory.com/278

[BOJ-11051][C++] 이항 계수 2

• https://dev-astra.tistory.com/279

[BOJ-1010][C++] 다리 놓기

 

참고 사이트

• https://ko.wikipedia.org/wiki/%EC%9D%B4%ED%95%AD_%EA%B3%84%EC%88%98

이항 계수 - 위키백과, 우리 모두의 백과사전

• https://ko.wikipedia.org/wiki/%ED%8C%8C%EC%8A%A4%EC%B9%BC%EC%9D%98_%EC%82%BC%EA%B0%81%ED%98%95

파스칼의 삼각형 - 위키백과, 우리 모두의 백과사전

• https://www.geeksforgeeks.org/binomial-coefficient-dp-9/

Binomial Coefficient | DP-9 - GeeksforGeeks

• https://moscowmule.tistory.com/6

[C][순환][반복] 이항 계수 계산