[Algorithm] 형상수(Figulate Number)

형상수(Figulate Number)

• 고대 그리스 시대의 피타고라스학파는 우주의 만물이 수로 이루어져 있다고 믿었다.
• 그래서 도형을 이용하여 숫자를 표현하였고, 수와 도형의 관계를 연구하였다.
• 이렇게 도형으로 묘사된 자연수를 형상수(Figulate Number)라고 한다.

 

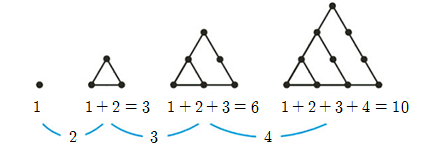
삼각수(Triangular Number)

개념

• 삼각형 모양으로 어떤 점을 놓았을 때, 삼각형을 이루기 위해 사용된 점의 개수

첫 번째 삼각수는 1, 두 번째 삼각수는 3(=1 + 2), 세 번째 삼각수는 6(=1 + 2 + 3)이다.

 

알고리즘

• 삼각수는 연속하는 자연수의 합과 같으며, 공식은 다음과 같다.

$$1 + 2 + 3 + \cdots + n = \frac{n × (n+1)}{2}$$

 

• 코드로 나타내면 다음과 같다.

			
			
			
		
#include <iostream>
using namespace std;
 
int main() {
    int a[6];
    
    for (int i = 1; i < 6; i++) {
        a[i] = (1 + i) * i / 2;
    }
    
    for (int i = 1; i < 6; i++) {
        cout << a[i] << '\n';
    }
    
    return 0;
}

			
			
			
		
0
1
3
6
10
15

 

사각수(Square Number)

개념

• 사각형 모양으로 어떤 점을 놓았을 때, 사각형을 이루기 위해 사용된 점의 개수
• 정사각수라고도 한다.

첫 번째 사각수는 1, 두 번째 사각수는 4(=2 × 2), 세 번째 사각수는 9(=3 × 3)이다.

 

알고리즘

• 사각수는 어떤 자연수를 제곱하여 얻어지는 수와 같으며, 공식은 다음과 같다.

$$n^{2}$$

 

• 코드로 나타내면 다음과 같다.

			
			
			
		
#include <iostream>
using namespace std;
 
int main() {
    int a[6];
    
    for (int i = 1; i < 6; i++) {
        a[i] = i * i;
    }
    
    for (int i = 1; i < 6; i++) {
        cout << a[i] << '\n';
    }
    
    return 0;
}

			
			
			
		
0
1
4
9
16
25

 

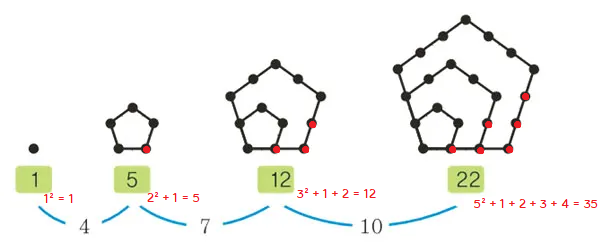
오각수(Pentagonal Number)

개념

• 오각형 모양으로 어떤 점을 놓았을 때, 오각형을 이루기 위해 사용된 점의 수

첫 번째 오각수는 1, 두 번째 오각수는 5, 세 번째 오각수는 12이다.

 

알고리즘

• 오각수는 어떤 자연수를 제곱한 것과 연속하는 자연수의 합과 같으며, 공식은 다음과 같다.

$$n^{2} + \frac{n × (n-1)}{2}$$

 

• 코드로 나타내면 다음과 같다.

			
			
			
		
#include <iostream>
using namespace std;
 
int main() {
    int a[6];
    
    for (int i = 1; i < 6; i++) {
        a[i] = (i * i) + i * (i - 1) / 2;
    }
    
    for (int i = 1; i < 6; i++) {
        cout << a[i] << '\n';
    }
    
    return 0;
}

			
			
			
		
0
1
5
12
22
35

 

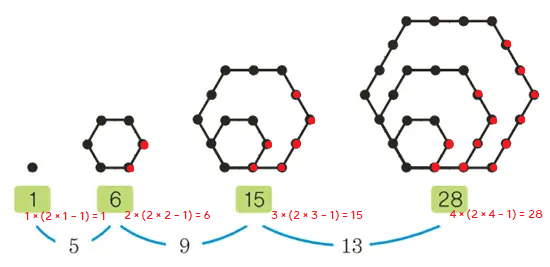
육각수(Hexagonal Number)

개념

• 육각형 모양으로 어떤 점을 놓았을 때, 육각형을 이루기 위해 사용된 점의 수

첫 번째 육각수는 1, 두 번째 육각수는 6, 세 번째 육각수는 15이다.

 

알고리즘

• 육각수의 공식은 다음과 같다.

$$n × (2 × n - 1)$$

 

• 코드로 나타내면 다음과 같다.

			
			
			
		
#include <iostream>
using namespace std;
 
int main() {
    int a[6];
    
    for (int i = 1; i < 6; i++) {
        a[i] = i * (2 * i - 1);
    }
    
    for (int i = 1; i < 6; i++) {
        cout << a[i] << '\n';
    }
    
    return 0;
}

			
			
			
		
1
6
15
28
45

 

삼각뿔수(Pyramidal Number)

개념

• 삼각뿔 모양으로 어떤 점을 놓았을 때, 삼각뿔을 이루기 위해 사용된 점의 수

첫 번째 삼각뿔수는 1, 두 번째 삼각뿔수는 4, 세 번째 삼각뿔수는 10이다.

 

알고리즘

• 삼각뿔수는 3, 6, 9 ....씩 증가하는 규칙성이 있으며, 공식은 다음과 같다.

$$1 + 3 × \frac{n×(n-1)}{2}$$

 

• 코드로 나타내면 다음과 같다.

			
			
			
		
#include <iostream>
using namespace std;
 
int main() {
    int a[6];
    
    for (int i = 1; i < 6; i++) {
        a[i] = 1 + 3 * i * (i - 1) / 2;
    }
    
    for (int i = 1; i < 6; i++) {
        cout << a[i] << '\n';
    }
    
    return 0;
}

			
			
			
		
1
4
10
19
31