728x90
728x90
피보나치 수열(Fibonacci Sequence)
레오나르도 피보나치(1170 ~ 1250, Leonardo Fibonacci)

레오나르도 피보나치(1170 ~ 1250, Leonardo Fibonacci)는 1170년 상업 도시인 이탈리아의 피사에서 태어났다. 그의 아버지는 피사에서 탁월한 상인으로 지중해에서 강력한 권력을 가진 사람 중 한 명이었다. 그의 아버지가 북부 아프리카의 통상 무역 대표로 임명받자, 북부 아프리카로 아들을 데려가 최신 이슬람 수학을 배울 수 있도록 하였다. 피보나치는 이집트, 시리아, 그리스, 시칠리아와 프로방스에서 다양한 공부를 하였고, 그곳에서 인도의 기수법과 아라비아 숫자를 사용하여 10진법으로 계산하는 것을 알게 되었다. 피보나치는 이런 다양한 경험을 살려서 피사로 돌아와 위대한 저서 『산반서』를 1202년에 완성하였다. 당시의 사람들은 주판을 사용하여 계산하고 로마 숫자로 기록하는 주산파와 새로운 숫자를 사용하는 알고리즈미(Algorismi) 기수법 파로 나뉘어 있었다. 대중들은 친숙 하지 않은 숫자에 반대하였고, 공무원들의 저항도 있었다. 알고리즈미 기수법은 14세기가 되어서야 널리 쓰이게 되었다. 피보나치는 그리스 수학자인 디오판토스와 유클리드와 같은 고대 수학자들의 업적을 향상시켰고, 정수론, 상업 수학의 실용 문제, 대수학에서의 응용 문제 등을 저술하였다.
피보나치 수열(Fibonacci Sequence)
- 사실 피보나치 수가 처음 언급된 문헌은 기원전 5세기 인도의 수학자 핑갈라(Pingala)가 쓴 책이다.
- 유럽에서 피보나치 수가 처음 등장한 것은 12세기 말에 쓰여진 『산반서』인데, 3부에는 다음과 같이 유명한 피보나치 문제가 실려 있다.
■ 1월 1일에 태어난 암수 한 쌍의 토끼가 있다.
■ 모든 달의 길이는 동일하다고 가정한다.
■ 한 쌍의 토끼는 태어난 지 두 달이 지나면 매달 두 마리의 새끼(암수 한 쌍)를 낳는다. 즉, 첫 번째 쌍은 3월 1일에 처음으로 두 마리의 새끼를 낳는다.
■ 그들에게서 태어난 새끼들도 두 달이 지나면서 짝을 이루어 매달 두 마리(암수 한 쌍)의 새끼를 낳는다.
■ 어떠한 토끼도 중간에 죽지 않는다.
■ 일 년 후에 전체 토끼는 모두 몇 쌍일까?
| 1월 | 2월 | 3월 | 4월 | 5월 | 6월 | 7월 | 8월 | 9월 | 10월 | 11월 | 12월 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
- 1월에 1쌍의 토끼가 있고, 2월에도 (새로 태어나는 토끼가 없으므로) 1쌍의 토끼가 있다. 3월에는 1월에 의해서 새로 태어나는 토끼 1쌍과 기존에 있던 토끼 1쌍을 더해서 모두 2쌍의 토끼가 있고, 4월에는 2월에 있던 토끼들이 새끼를 낳기 때문에 새로 태어나는 토끼 1쌍과 기존에 있던 토끼 2쌍을 더해서 모두 3쌍의 토끼가 된다. 5월은 3월에 있던 토끼가 2쌍을 낳고, 기존에 있던 토끼 3쌍을 합쳐서 모두 5쌍의 토끼가 된다.
- 이와 같이 열의 앞의 두 수를 합한 것이 현재 열의 수가 되는 규칙이 있다.
- 이 문제의 풀이에 나오는 이와 같은 수열을 루카스라는 수학자가 피보나치 수열(Fibonacci Sequence)이라고 이름을 붙였다.
구현
#include <iostream>
using namespace std;
int main() {
int a[13] = { 0, 1 };
for (int i = 2; i <= 12; i++) {
a[i] = a[i - 1] + a[i - 2];
}
for (int i = 1; i <= 12; i++) {
cout << a[i] << " ";
}
return 0;
}더보기
1 1 2 3 5 8 13 21 34 55 89 144
재귀 함수를 이용하여 구현하기
int Fibonacci(int n) {
if (n == 0) return 0;
else if (n == 1) return 1;
return Fibonacci(n - 2) + Fibonacci(n - 1);
}
자연속의 피보나치 수열
- 자연속에는 수 많은 수학적인 사실들이 있는데, 그 중에서도 가장 대표적인 것이 피보나치 수열이다.
- 몇몇 꽃잎을 제외하고 대부분의 꽃잎의 수는 피보나치 수로 이루어져 있다.
- 예)
- 분꽃과 백합 : 3장
- 채송화와 벚꽃 : 5장
- 코스모스와 모란 : 8장
- 금진화 : 13장
- 치커리 : 21장
- 데이지 : 34장
- 들국화 : 55장 또는 89장
- 식물들이 이렇게 피보나치 수열을 이루고 있는 이유는 햇빛을 받을 때 유리하고, 이렇게 피보나치 수열을 이룰 때 꽃잎이 활짝 피기 전까지 암술과 수술을 잘 보호할 수 있기 때문이라고 한다. 또한 번식을 위해 벌들이나 나비들을 유인할 때, 피보나치 수로 이루어져 있어야 더 잘 유인할 수 있다는 사실도 밝혀졌다.
- 예)
- 해바라기 씨에도 피보나치 수열이 숨어져 있다고 한다. 해바라기 씨는 오른쪽과 왼쪽으로 도는 두 가지 나선이 있는데, 좌우 나선의 수를 살펴보면 하나가 21이고 다른 하나는 34이다.
- 만약 하나가 34라면 다른 하나는 55라는 식으로 피보나치 수로 구성되어 있다는 것을 확인할 수 있다.
피보나치 수열과 황금비(Golden Ratio)
- 황금 비율(Golden Ratio)이란, 인간의 눈에 가장 안정적으로 보이는 비율을 의미하며 그리스의 수학자 유클리드(Euclid)가 구체화 시키면서 널리 알려지게 되었다.
- 유클리드는 황금비가 "한 선분을 전체 직선과 긴 선분의 비가 긴 선분과 짧은 선분의 비와 같도록 나누는 것" 이라고 정의하였다.
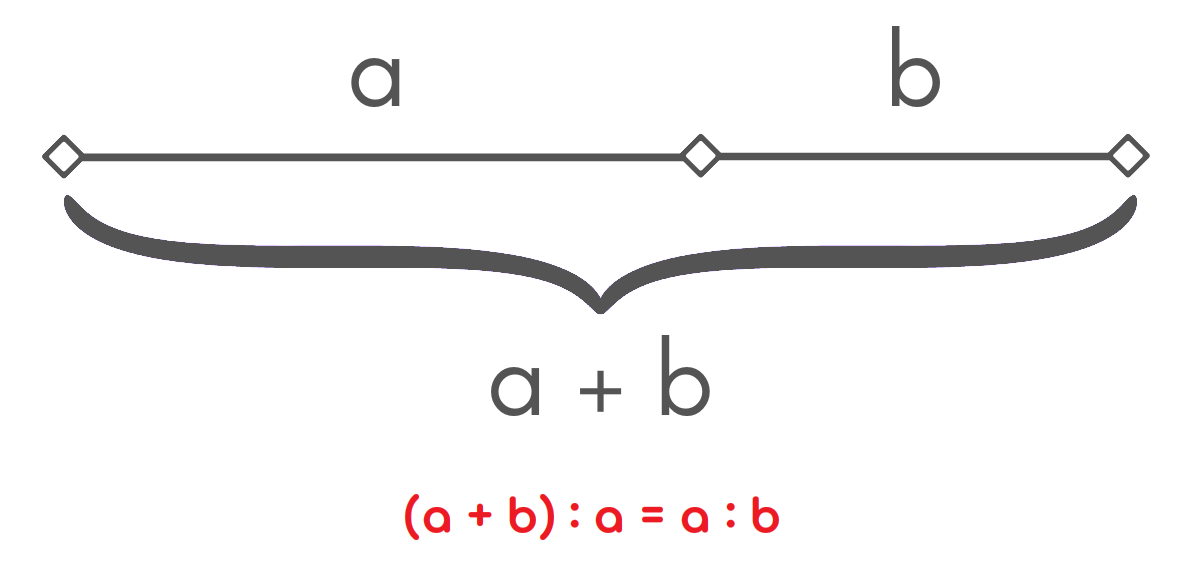
- 이 정해진 비율을 소수점으로 나타내면 1.61803398… 과 같고, 소수점 셋째 자리까지 나타내면 1.618인데, 이 1.618을 황금비라고 말한다.
- 황금비는 고대 건축물 파르테논 신전에서도 찾아볼 수 있다.
- 신전의 높이와 폭의 비가 약 1 : 1.618 이고, 기둥과 지붕의 비 역시 1 : 1.618로 황금비로 이루어져 있다.
- 피보나치 수열은 황금비와도 관계가 있다.
- 피보나치 수열의 앞의 수를 바로 이웃한 수로 나누어 보면 1 ÷ 1 = 1, 2 ÷ 1 = 2, 3 ÷ 2 = 1.5, 5 ÷ 3 = 1.666, 8 ÷ 5 = 1.6, 13 ÷ 8 = 1.625 가 되며, 이 값은 점점 황금비인 1.61803398… 에 근접하게 된다.
728x90
728x90
'Computer Science > 알고리즘' 카테고리의 다른 글
| [Algorithm] 부분합(Partial Sum) ; 누적합(Prefix Sum) (0) | 2022.10.26 |
|---|---|
| [Algorithm] 형상수(Figulate Number) (0) | 2022.10.26 |
| [Algorithm] 에라토스테네스의 체(Sieve of Erathosthenes) (0) | 2022.10.25 |
| [Algorithm] 소인수 분해(Prime/Integer Factorization) (0) | 2022.10.25 |
| [Algorithm] 삽입 정렬(Insertion Sort) (1) | 2022.10.06 |
| [Algorithm] 버블 정렬(Bubble Sort) (0) | 2022.10.06 |
| [Algorithm] 선택 정렬(Selection Sort) (0) | 2022.10.06 |
| [Algorithm] 최대(Max), 최소(Min), 최빈(Mode) (0) | 2022.10.06 |
