728x90
728x90
행렬과 연립 일차 방정식
- 행렬은 연립 일차 방정식을 풀기 위한 방법을 연구하면서 나온 개념이다.
일차 방정식(Linear Equation) / 선형 방정식
$a_{1}, a_{2}, \cdots, a_{n}, b$ 가 실수일 때, 다음과 같이 표현되는 식
$$a_{1}x_{1} + a_{2}x_{2} + \cdots + a_{n}x_{n} = b \quad (a_{1}, a_{2}, \cdots, a_{n} : \text{계수}, \; b : \text{상수}, \; x_{1}, x_{2}, \cdots, x_{n} : \text{변수})$$
- 문제를 해결하기 위한 어떤 식이 한 개 이상의 변수를 포함할 때 이 식을 방정식(Equation)이라고 하며, 포함하는 변수의 차수가 1일 때 이를 일차 방정식 또는 선형 방정식이라고 한다.
- 일차 방정식은 모든 미지수의 차수가 1이어야 한다.
- 예)
- $x + 27 - z = 0$
- $\frac{1}{3}x = 3y$
- $x_{1} - x_{2} + 4x_{3} = 0$
- 예)
- 서로 다른 변수 간의 곱이 포함된 방정식은 일차 방정식이 아니다.
- 예)
- $xy - 4z = 8$
- $xyz = 2$
- 예)
- 삼각 함수, 로그 함수 등을 포함하는 방정식도 일차 방정식이 아니다.
- 예)
- $y = \sin x$
- $\log_{2}y = 20$
- 예)
해(Solution)와 해집합(Solution Set)
일차 방정식에 포함된 `n` 개의 변수에 대응하는 값으로, 방정식을 참(T)으로 만드는 값과 그 값의 집합
- 일차 방정식 $a_{1}x_{1} + a_{2}x_{2} + \cdots + a_{n}x_{n} = b$ 에 대하여, 이 방정식의 변수에 대입하였을 때 방정식을 참(T)으로 만드는 유일한 값, $x_{1} = s_{1}, \; x_{2} = s_{2}, \; \cdots, \; x_{n} = s_{n}$ 이 존재할 수 있다.
- 이 $s_{1}, s_{2}, \cdots, s_{n}$ 을 이 방정식의 해 또는 해집합이라고 한다.
- 일차 방정식이 변수 하나만 포함하는 경우 유일한 해를 구하기 위해 하나의 방정식만 있으면 되지만, 변수를 2개 이상 포함한다면 동일한 변수를 갖는 방정식도 2개 이상 있어야 방정식의 유일한 해를 구할 수 있다.
- 이처럼 2개 이상의 변수로 구성된 일차 방정식의 유한개의 집합을 연립 일차 방정식이라고 한다.
연립 일차 방정식(System of Linear Equations)
`m` 개의 일차 방정식으로 구성된 방정식
$$\begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots + a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} = b_{2} \\ \cdots \\ a_{m1}x_{1} + a_{m2}x_{2} + \cdots + a_{mn}x_{n} = b_{m} \end{cases} $$
- 연립 일차 방정식에 포함된 방정식의 개수는 방정식으로 해결해야 하는 문제의 종류에 따라 달라질 수 있다.
- 연립 일차 방정식에 포함된 방정식의 개수와 방정식에 포함되는 변수의 개수가 항상 같지는 않다.
- 방정식의 개수 `m` 과 변수의 개수 `n` 에 대하여 $m ≠ n$ 일 수 있다.
- 단, `m = n` 인 경우, 연립 일차 방정식의 각 변수에 대응하는 유일한 해를 구할 수 있다.
- 연립 일차 방정식에 포함된 방정식의 개수와 방정식에 포함되는 변수의 개수가 항상 같지는 않다.
- 이 페이지에서는 `m = n` 인 경우만을 다루도록 한다.
연립 일차 방정식의 행렬 표현
- 연립 일차 방정식의 해를 구하는 방법에는 가감법이나 대입법과 같이 변수를 소거하거나 하나의 방정식을 다른 방정식에 대입하는 방법도 있으나, 행렬을 이용하는 방법도 있다.
`m` 개의 일차 방정식으로 구성된 연립 일차 방정식의 행렬 표현
① 계수 행렬(Coefficient Matrix) : 연립 일차 방정식의 계수들로 구성된 $m × n$ 행렬
$$A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$$
② 미지수 행렬(Unknown Value Matrix) : 연립 일차 방정식의 미지수들로 구성된 $n × 1$ 행렬
$$X = \begin{bmatrix} x_{1} \\ x_{2} \\ \cdots \\ x_{n} \end{bmatrix}$$
③ 상수 행렬(Constant Matrix) : 연립 일차 방정식의 상수들로 구성된 $m × 1$ 행렬
$$B = \begin{bmatrix} b_{1} \\ b_{2} \\ \cdots \\ b_{m} \end{bmatrix}$$
- 위에서 정의한 행렬로 연립 일차 방정식을 표현하면 다음과 같다.
$$AX = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \cdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} b_{1} \\ b_{2} \\ \cdots \\ b_{m} \end{bmatrix} = B$$
- 연립 일차 방정식의 해를 구하기 위해 위에서 정의한 행렬을 이용하여 첨가 행렬을 구성할 수 있다.
첨가 행렬(Augmented Matrix)
연립 일차 방정식의 계수 행렬 `A` 와 상수 행렬 `B` 를 다음과 같은 형태로 구성한 행렬
$$\left[ \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_{1} \\ a_{21} & a_{22} & \cdots & a_{2n} & b_{2} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_{m} \end{array} \right] $$
예
- 다음과 같은 연립 일차 방정식이 있다고 하자.
| $$\begin{cases} x + 2y + 3z = 1 \\ x + 3y + 6z = 1 \\ 2x + 6y + 13z = 5 \end{cases}$$ |
- 이 연립 일차 방정식을 구성하는 요소들을 행렬로 표현하면 다음과 같다.
| 계수 행렬 $A = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 3 & 6 \\ 2 & 6 & 13 \end{bmatrix}$, 미지수 행렬 $X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}$, 상수 행렬 $B = \begin{bmatrix} 1 \\ 1 \\ 5 \end{bmatrix}$ |
- 이 행렬들을 이용하여 첨가 행렬을 구하면 다음과 같다.
| $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 1 & 3 & 6 & 1 \\ 2 & 6 & 13 & 5 \end{array} \right]$ |
행 사다리꼴 행렬(Row Echelon Form Matrix ; REFM)과 기약 행 사다리꼴 행렬(Reduced Row Echelon Form Matrix ; RREFM)
- 행렬을 이용하여 연립 일차 방정식의 해를 구하는 방법으로 가우스 소거법과 가우스-조단 소거법이 있다.
- 두 방법은 거의 동일하며, 가우스 소거법에서 과정을 조금 더 진행하면 가우스-조단 소거법인데, 이 과정에서 필요한 행렬이 행 사다리꼴 행렬과 기약 행 사다리꼴 행렬이다.
① 행 사다리꼴 행렬(Row Echelon Form Matrix) : 각 행의 0이 아닌 첫 번째 원소가 1이고, 그 1을 포함하는 열에서 1의 아래쪽 원소가 모두 0인 행렬
② 기약 행 사다리꼴 행렬(Reduced Row Echelon Form Matrix) : 행 사다리꼴 행렬에서 각 행의 0이 아닌 첫 번째 원소 1을 포함한 열의 나머지 원소가 모두 0인 행렬
 |
 |
- 어떤 행렬이 행 사다리꼴 행렬이라면 다음 조건을 만족해야 한다.
① 어떤 행은 1열부터 0으로 구성된다.
② 모든 행의 0이 아닌 첫 번째 원소(◆)는 1이다.
③ 모든 행의 0이 아닌 첫 번째 원소(◆)는 상위 행의 0이 아닌 첫 번째 원소보다 오른쪽 열에 위치한다.
④ 모든 원소가 0인 행이 있다면 행렬의 가장 마지막 행에 위치한다.
- 위의 네 가지 조건을 만족하면 행 사다리꼴 행렬은 대각선의 왼쪽 아래 부분이 모두 0으로 구성된다.
- 어떤 행렬이 기약 행 사다리꼴 행렬이라면 다음 조건을 만족해야 한다.
① 각 행에서 처음으로 0이 아닌 선행 성분은 1이다.
② 각 행의 선행 성분 1의 위/아래 성분이 모두 0이다.
예 : 행 사다리꼴 행렬
| $$A = \begin{bmatrix} 1 & -5 & 9 & 1 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 0 & 1 & 6 & 7 \\ 0 & 0 & 1 & 9 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 2 & -3 & 1 \\ 0 & 0 & 1 & 7 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & -3 \end{bmatrix}, \quad D = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 0 & 5 & 6 & 7 \\ 0 & 0 & 8 & 9 \end{bmatrix}$$ |
- 행렬 `A` 는 행 사다리꼴 행렬이다.
- 4행은 1열부터 0으로 구성된다. (조건 ① 만족)
- 각 행의 0이 아닌 첫 번째 원소가 모두 1이다. (조건 ② 만족)
- 각 행의 0이 아닌 첫 번째 원소 1은 상위 행의 0이 아닌 첫 번째 원소 1보다 오른쪽 열에 위치한다. (조건 ③ 만족)
- 모든 원소가 0인 행은 가장 마지막 행에 위치한다. (조건 ④ 만족)
- 행렬 `B` 도 모든 원소가 0인 행이 없을 뿐, 다른 모든 조건을 만족하므로 행 사다리꼴 행렬이다.
- 행렬 `C` 는 행 사다리꼴 행렬이 아니다.
- 4행의 0이 아닌 첫 번째 원소가 2행과 3행의 0이 아닌 첫 번째 원소보다 왼쪽 열에 있다. (조건 ③ 위배)
- 행렬 `D` 는 행 사다리꼴 행렬이 아니다.
- 2행과 3행의 0이 아닌 첫 번째 원소가 1이 아니다. (조건 ② 위배)
예 : 기약 행 사다리꼴 행렬
| $$A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 6 \\ 0 & 0 & 1 & 3 \end{bmatrix}$$ |
- 기약 행 사다리꼴 행렬은 행 사다리꼴 행렬의 조건을 만족하면서, 각 행의 0이 아닌 첫 번째 원소 1을 포함한 열의 나머지 원소가 모두 0인 행렬을 의미한다.
- 따라서 위의 행렬은 모두 기약 행 사다리꼴 행렬이다.
가우스 소거법(Gaussian Elimination)
- 주어진 첨가 행렬을 행 사다리꼴 행렬로 변환하고, 그렇게 변환한 첨가 행렬을 다시 연립 일차 방정식으로 만들어 후진 대입법으로 값을 대입하면서 해를 구한다.
후진 대입법(Backward Substitution)
- 가우스 소거법으로 얻은 행 사다리꼴 행렬을 이용하여 연립 일차 방정식을 구성하면, 다음 연립 일차 방정식의 식 ③ $x_{3} = b_{3}$ 처럼 미지수가 하나인 방정식을 얻는다.
| $$\begin{cases} x_{1} + a_{12}x_{2} + a_{13}x_{3} = b_{1} \; \cdots \; ① \\ \hfill x_{2} + a_{23}x_{3} = b_{2} \; \cdots \; ② \\ \hfill x_{3} = b_{3} \; \cdots \; ③ \end{cases}$$ |
- 그러면 미지수 `x_{3}` 가 `b_{3}` 임을 알 수 있다.
- `x_{3}` 의 값을 식 ②에 대입하여 `x_{2}` 의 값 `b_{2} - a_{23}b_{3}` 을 구하고, `x_{2}, x_{3}` 의 값을 식 ①에 대입하여 `x_{1}` 의 값 `b_{1} - a_{12}(b_{2} - a_{23}b_{3}) - a_{13}b_{3}` 을 구할 수 있다.
- 이처럼 연립 일차 방정식의 가장 아래에 있는 방정식에서 마지막 미지수의 값을 구하기 시작하여 한 단계씩 위쪽에 있는 미지수의 해를 구하는 방법을 후진 대입법이라고 한다.
기본 행 연산(Elementary Row Operation)
- 가우스 소거법을 이용하여 첨가 행렬을 행 사다리꼴 행렬(또는 기약 행 사다리꼴 행렬)로 만드는 과정을 기본 행 연산이라고 하며, 다음의 과정으로 진행 된다.
① 한 행에 0이 아닌 스칼라를 곱한다.
② 스칼라곱을 한 행을 다른 행에 더한다.
※ 필요에 따라 행의 위치를 교환할 수도 있다.
예 : 연립 일차 방정식 $\begin{cases} x + 2y + 3z = 1 \\ x + 3y + 6z = 1 \\ 2x + 6y + 13z = 5 \end{cases}$ 의 해를 가우스 소거법으로 구하기
- 주어진 연립 일차 방정식의 첨가 행렬은 다음과 같다.
| $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 1 & 3 & 6 & 1 \\ 2 & 6 & 13 & 5 \end{array} \right]$ |
- 이 첨가 행렬에서 초록색 부분을 1로 만들고, 주황색 부분을 0으로 만들면 행 사다리꼴 행렬이 된다.
| $\left[ \begin{array}{ccc|c} \color{green}{1} & 2 & 3 & 1 \\ \color{orange}{1} & \color{green}{3} & 6 & 1 \\ \color{orange}{2} & \color{orange}{6} & \color{green}{13} & 5 \end{array} \right]$ |
(1) 1행 1열 원소는 이미 1이다.
(2) 2행 1열 원소와 3행 1열 원소를 0으로 만들기 위해 이미 1인 1행 1열 원소를 이용하여 다음과 같이 연산한다. 이 때, 2행과 3행 연산 결과를 얻은 후 연산의 기준인 1행은 원래대로 작성한다.
① 2행 1열 원소를 0으로 만들기 위해, $(2행) = (1행) × (-1) + (2행)$
과정 결과 (1행) × (-1) $\left[ \begin{array}{ccc|c} -1 & -2 & -3 & -1 \\ 1 & 3 & 6 & 1 \\ 2 & 6 & 13 & 5 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & 1 & 3 & 0 \\ 2 & 6 & 13 & 5 \end{array} \right]$ 1행 : 원래대로 작성
2행 : (1행) × (-1) + (2행)
② 3행 1열 원소를 0으로 만들기 위해, $(3행) = (1행) × (-2) + (3행)$
과정 결과 (1행) × (-2) $\left[ \begin{array}{ccc|c} -2 & -4 & -6 & -2 \\ 0 & 1 & 3 & 0 \\ 2 & 6 & 13 & 5 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & 1 & 3 & 0 \\ 0 & 2 & 7 & 3 \end{array} \right]$ 1행 : 원래대로 작성
3행 : (1행) × (-2) + (3행)
①, ②에서 구한 첨가 행렬의 결과를 보면 2행 1열의 원소는 0, 2행 2열의 원소는 1이다.
③ 3행 2열 원소를 0으로 만들기 위해, $(3행) = (2행) × (-2) + (3행)$
③에서 구한 첨가 행렬은 행 사다리꼴 행렬 형태이다.
과정 결과
(2행) × (-2)$\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & -2 & -6 & 0 \\ 0 & 2 & 7 & 3 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \end{array} \right]$
2행 : 원래대로 작성
3행 : (2행) × (-2) + (3행)
마지막 첨가 행렬에서 계수 행렬은 $\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{bmatrix}$, 상수 행렬은 $\begin{bmatrix}1 & 0 & 3 \end{bmatrix}$, 미지수 행렬은 $\begin{bmatrix}x & y & z \end{bmatrix}$ 이고, 이를 이용하여 다시 연립 일차 방정식을 표현하면 다음과 같다.
$$\begin{cases} x + 2y + 3z = 1 \\ \hfill y + 3z = 0 \\ \hfill z = 3 \end{cases}$$
위 연립 방정식에서 `z` 를 이용하여 `y` 를 구하고, `y, z` 를 이용하여 `x` 를 구한다. (이 방법이 후진 대입법이다.)
`z = 3` 을 `y + 3z = 0` 에 대입하면 다음과 같다.
$$y + 3 × 3 = y + 9 = 0 \quad ∴ y = -9$$
`y = -9, z = 3` 을 `x + 2y + 3z = 1` 에 대입하면 다음과 같다.
$$x + 2 × (-9) + 3 × 3 = 1, \quad ∴ x = 10$$
그러므로 이 연립 일차 방정식의 해는 `x = 10, y = -9, z = 3` 이다.
예 : 연산의 편의를 위해서 행의 순서를 바꾸는 경우
- 다음과 같은 첨가 행렬이 있다고 가정하자.
| $\left[ \begin{array}{ccc|c} 0 & 2 & 3 & 7 \\ 2 & 6 & 8 & 10 \\ \color{red}{1} & 5 & 6 & 1 \end{array} \right]$ |
- 이 첨가 행렬의 1행 1열 원소가 0이므로 이 형태로는 행 사다리꼴 행렬을 만들 수 없다. 마침 3행 1열의 원소가 1이므로, 1행과 3행의 자리를 바꾸면 행 사다리꼴 행렬 형태를 만들기 쉽다.
| $\left[ \begin{array}{ccc|c} 1 & 5 & 6 & 1 \\ 2 & 6 & 8 & 10 \\ 0 & 2 & 3 & 7 \end{array} \right]$ |
- 이 첨가 행렬을 이용하여 행 사다리꼴 행렬을 만들어 연립 일차 방정식의 해를 구해보자.
① 2행 1열 원소를 0으로 만들기 위해, $(2행) = (1행) × (-2) + (2행)$
과정 결과 (1행) × (-2) $\left[ \begin{array}{ccc|c} -2 & -10 & -12 & -2 \\ 2 & 6 & 8 & 10 \\ 0 & 2 & 3 & 7 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 5 & 6 & 1 \\ 0 & -4 & -4 & 8 \\ 0 & 2 & 3 & 7 \end{array} \right]$ 1행 : 원래대로 작성
2행 : (1행) × (-2) + (2행)
② 2행 2열 원소를 1로 만들기 위해, $(2행) = (2행) × (-\frac{1}{4})$
$\left[ \begin{array}{ccc|c} 1 & 5 & 6 & 1 \\ 0 & 1 & 1 & -2 \\ 0 & 2 & 3 & 7 \end{array} \right]$
2행 : (2행) × $(-\frac{1}{4})$
③ 3행 2열 원소를 0으로 만들기 위해, $(3행) = (2행) × (-2) + (3행)$
과정 결과
(2행) × (-2)$\left[ \begin{array}{ccc|c} 1 & 5 & 6 & 1 \\ 0 & -2 & -2 & 4 \\ 0 & 2 & 3 & 7 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 5 & 6 & 1 \\ 0 & 1 & 1 & -2 \\ 0 & 0 & 1 & 11 \end{array} \right]$
2행 : 원래대로 작성
3행 : (2행) × (-2) + (3행)
결과로 나온 첨가 행렬은 행 사다리꼴 행렬이다. 이 행렬을 이용하여 다시 연립 일차 방정식을 표현하면 다음과 같다.
$$\begin{cases} x + 5y + 6z = 1 \\ \hfill y + z = -2 \\ \hfill z = 11 \end{cases}$$
후진 대입법을 이용해 해를 구해보자.
`z = 11` 을 `y + z = -2` 에 대입하면 다음과 같다.
$$y + 11 = -2 \quad ∴ y = -13$$
`y = -13, z =11` 을 `x + 5y + 6z = 1` 에 대입하면 다음과 같다.
$$x + 5 × (-13) + 6 × 11 = 1 \quad ∴ x = 0$$
그러므로 이 연립 일차 방정식의 해는 `x = 0, y = -13, z =11` 이다.
가우스-조단 소거법(Gauss-Jordan Elimination)
- 첨가 행렬의 계수 행렬 부분을 기약 행 사다리꼴 행렬로 만들어 해를 구하는 방법
- 가우스-조단 소거법을 모두 마친 후, 최종 첨가 행렬의 형태는 다음과 같다.
$$\left[ \begin{array}{ccccccc|c} 1 & a_{1i} & \cdots & a_{1j} & a_{1k} & \cdots & a_{1n} & s_{1} \\ 0 & 1 & \cdots & a_{2j} & a_{2k} & \cdots & a_{2n} & s_{2} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 & a_{mk} & \cdots & a_{mn} & s_{m} \end{array} \right]$$
- 그런데 이 페이지에서는 방정식의 개수와 방정식을 구성하는 미지수의 개수가 같은($m = n$) 연립 일차 방정식만 다루기로 했으므로, 여기서 가우스-조단 소거법을 이용하여 기약 행 사다리꼴로 만들면 첨가 행렬의 계수 행렬 부분은 단위 행렬 $I$ 가 될 것이다.
- 일반적으로 가우스-조단 소거법은 가우스 소거법에서 몇 단계의 연산 과정을 더 진행한다.
예 : 연립 일차 방정식 $\begin{cases} x + 2y + 3z = 1 \\ x + 3y + 6z = 1 \\ 2x + 6y + 13z = 5 \end{cases}$ 의 해를 가우스-조단 소거법으로 구하기
- 행 사다리꼴 행렬은 다음과 같다.
| $\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \end{array} \right]$ |
- 위의 첨가 행렬에서 계수 행렬 부분을 기약 행 사다리꼴 행렬로 만들기 위해 가우스 소거법과 같은 방식으로 연산한다.
① 1행 2열 원소를 0으로 만들기 위해, $(1행) = (2행) × (-2) + (1행)$
과정 결과
(2행) × (-2)$\left[ \begin{array}{ccc|c} 1 & 2 & 3 & 1 \\ 0 & -2 & -6 & 0 \\ 0 & 0 & 1 & 3 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 0 & -3 & 1 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \end{array} \right]$
1행 : (2행) × (-2) + (1행)
2행 : 원래대로 작성
② 1행 3열 원소를 0으로 만들기 위해, $(1행) = (3행) × 3 + (1행)$③ 2행 3열 원소를 0으로 만들기 위해, $(2행) = (3행) × (-3) + (2행)$
과정 결과
(3행) × 3$\left[ \begin{array}{ccc|c} 1 & 0 & -3 & 1 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 3 & 9 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 10 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \end{array} \right]$
1행 : (3행) × 3 + (1행)
3행 : 원래대로 작성
과정 결과
(3행) × (-3)$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 10 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & -3 & -9 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 10 \\ 0 & 1 & 0 & -9 \\ 0 & 0 & 1 & 3 \end{array} \right]$
2행 : (3행) × (-3) + (2행)
3행 : 원래대로 작성
마지막 첨가 행렬에서 계수 행렬은 $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$, 상수 행렬은 $\begin{bmatrix} 10 \\ -9 \\ 3 \end{bmatrix}$ 이다. 미지수 행렬을 $\begin{bmatrix} x \\ y \\ z \end{bmatrix}$ 라고 할 때, 다음과 같이 나타낼 수 있다.
$$AX = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} × \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 10 \\ -9 \\ 3 \end{bmatrix}$$
따라서 이 연립 일차 방정식의 해는 `x = 10, y = -9, z = 3` 이다.
가우스-조단 소거법으로 구하는 역행렬
- 가역 행렬인 경우에는 가우스-조단 소거법을 이용하여 역행렬을 구할 수 있다.
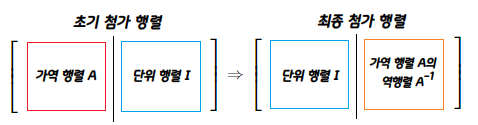
- 첨가 행렬의 왼쪽에 가역 행렬, 오른쪽에 단위 행렬을 놓고 첨가 행렬의 왼쪽 부분이 단위 행렬 형태가 될 때까지 가우스-조단 소거법을 수행하면 오른쪽 부분의 행렬이 처음 왼쪽에 놓은 가역 행렬의 역행렬이 된다.
예 : 행렬 $A = \begin{bmatrix} -2 & 2 & 3 \\ 1 & 0 & 1 \\ -4 & 3 & -5 \end{bmatrix}$ 의 역행렬을 가우스-조단 소거법을 이용하여 구하기
- 첨가 행렬은 다음과 같다.
| $\left[ \begin{array}{ccc|ccc} -2 & 2 & -3 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ -4 & 3 & -5 & 0 & 0 & 1 \end{array} \right]$ |
① 첨가 행렬의 왼쪽 부분 2행 1열 원소가 1이므로 1행과 2행의 자리를 바꾼다.
$$\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ -2 & 2 & -3 & 1 & 0 & 0 \\ -4 & 3 & -5 & 0 & 0 & 1 \end{array} \right]$$
② 첨가 행렬의 왼쪽 부분 2행 1열 원소를 0으로 만들기 위해, $(2행) = (1행) × 2 + (2행)$
과정 결과 (1행) × 2 $\left[ \begin{array}{ccc|ccc} 2 & 0 & 2 & 0 & 2 & 0 \\ -2 & 2 & -3 & 1 & 0 & 0 \\ -4 & 3 & -5 & 0 & 0 & 1 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 2 & -1 & 1 & 2 & 0 \\ -4 & 3 & -5 & 0 & 0 & 1 \end{array} \right]$ 1행 : 원래대로 작성
2행 : (1행) × 2 + (2행)
③ 첨가 행렬의 왼쪽 부분 3행 1열 원소를 0으로 만들기 위해, $(3행) = (1행) × 4 + (3행)$
과정 결과 (1행) × 4 $\left[ \begin{array}{ccc|ccc} 4 & 0 & 4 & 0 & 4 & 0 \\ 0 & 2 & -1 & 1 & 2 & 0 \\ -4 & 3 & -5 & 0 & 0 & 1 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 2 & -1 & 1 & 2 & 0 \\ 0 & 3 & -1 & 0 & 4 & 1 \end{array} \right]$ 1행 : 원래대로 작성
3행 : (1행) × 4 + (3행)
④ 첨가 행렬의 왼쪽 부분 2행 2열 원소를 1로 만들기 위해, $(2행) = (2행) × $\frac{1}{2}$$
$\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 3 & -1 & 0 & 4 & 1 \end{array} \right]$
2행 : (2행) × $\frac{1}{2}$
⑤ 첨가 행렬의 왼쪽 부분 3행 2열 원소를 0으로 만들기 위해, $(3행) = (2행) × (-3) + (3행)$
과정 결과
(2행) × (-3)$\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & -3 & \frac{3}{2} & -\frac{3}{2} & -3 & 0 \\ 0 & 3 & -1 & 0 & 4 & 1 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 0 & \frac{1}{2} & -\frac{3}{2} & 1 & 1 \end{array} \right]$
2행 : 원래대로 작성
3행 : (2행) × (-3) + (3행)
⑥ 첨가 행렬의 왼쪽 부분 3행 3열 원소를 1로 만들기 위해, $(3행) = (3행) × 2$
$\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 0 & 1 & -3 & 2 & 2 \end{array} \right]$
3행 : (3행) × 2
⑦ 첨가 행렬의 왼쪽 부분 1행 3열 원소를 0으로 만들기 위해, $(1행) = (3행) × (-1) + (1행)$
과정 결과
(3행) × (-1)$\left[ \begin{array}{ccc|ccc} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 0 & -1 & 3 & -2 & -2 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & 3 & -1 & -2 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 0 & 1 & -3 & 2 & 2 \end{array} \right]$ 1행 : (3행) × (-1) + (1행)
3행 : 원래대로 작성
⑧ 첨가 행렬의 왼쪽 부분 2행 3열 원소를 0으로 만들기 위해, $(2행) = (3행) × \frac{1}{2} + (2행)$
과정 결과
(3행) × $\frac{1}{2}$$\left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & 3 & -1 & -2 \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} & 1 & 0 \\ 0 & 0 & \frac{1}{2} & -\frac{3}{2} & 1 & 1 \end{array} \right]$ $\Rightarrow$ $\left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & 3 & -1 & -2 \\ 0 & 1 & 0 & -1 & 2 & 1 \\ 0 & 0 & 1 & -3 & 2 & 2 \end{array} \right]$
2행 : (3행) × $\frac{1}{2}$ + (2행)
3행 : 원래대로 작성
첨가 행렬의 왼쪽 부분을 단위 행렬로 만들었다.
따라서 첨가 행렬의 오른쪽 부분은 행렬 `A` 의 역행렬이다.
728x90
728x90
'Mathematics > 이산 수학' 카테고리의 다른 글
| [이산 수학] 집합의 대수 법칙 (0) | 2022.10.22 |
|---|---|
| [이산 수학] 집합의 연산 (0) | 2022.10.22 |
| [이산 수학] 집합의 종류 (0) | 2022.10.22 |
| [이산 수학] 집합의 개념 (0) | 2022.10.22 |
| [이산 수학] 역행렬 (0) | 2022.10.12 |
| [이산 수학] 행렬식 (0) | 2022.10.12 |
| [이산 수학] 행렬의 종류 (0) | 2022.10.12 |
| [이산 수학] 행렬의 연산 (1) | 2022.10.11 |

