문제
크기가 N인 파스칼의 삼각형을 만들어야 한다.
파스칼의 삼각형이란 아래와 같은 규칙을 따른다.
1. 첫 번째 줄은 항상 숫자 1이다.
2. 두 번째 줄부터 각 숫자들은 자신의 왼쪽과 오른쪽 위의 숫자의 합으로 구성된다.
N이 4일 경우,
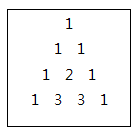
N을 입력 받아 크기 N인 파스칼의 삼각형을 출력하는 프로그램을 작성하시오.
제약 사항
파스칼의 삼각형의 크기 N은 1 이상 10 이하의 정수이다. (1 ≤ N ≤ 10)
입력
가장 첫 줄에는 테스트 케이스의 개수 T가 주어지고, 그 아래로 각 테스트 케이스가 주어진다.
각 테스트 케이스에는 N이 주어진다.
출력
각 줄은 '#t'로 시작하고, 다음 줄부터 파스칼의 삼각형을 출력한다.
삼각형 각 줄의 처음 숫자가 나오기 전까지의 빈 칸은 생략하고 숫자들 사이에는 한 칸의 빈칸을 출력한다.
(t는 테스트 케이스의 번호를 의미하며 1부터 시작한다.)
예제
| [입력] | [출력] |
| 1 4 |
#1 1 1 1 1 2 1 1 3 3 1 |
문제 해결 방법
- 파스칼 삼각형의 생성 규칙을 이해하면 가볍게 풀 수 있었던 문제였다.
1. 첫 번째 줄은 항상 숫자 1이다.
2. 두 번째 줄부터 각 숫자들은 자신의 왼쪽과 오른쪽 위의 숫자의 합으로 구성된다.

- 맨 꼭대기 층을 1번째 줄이라고 하고 밑으로 내려올 수록 2번째 줄, 3번째 줄, ...이라고 할 경우, N번째 줄의 경우 N개의 원소가 들어 있다.
- 1번째 줄에는 1개, 2번째 줄에는 2개, ..., N번째 줄에는 N개의 원소가 들어 있다.
- 우선 입력 받은 파스칼 삼각형의 높이 값(@H@)을 토대로 1층부터 H층까지 각 층을 @H@개의 @1@로 채워준다.
H = int(input())
# 높이가 H이고 1로 채워진 피라미드 모양의 배열을 만든다.
matrix = [[1] * i for i in range(1, H + 1)]
만약 H가 4일 경우, matrix 리스트의 내용은 [[1], [1, 1], [1, 1, 1], [1, 1, 1, 1]]로 구성된다.
리스트 안에 또 다른 리스트가 들어 있는 구조인데, 내부에 있는 각 리스트는 각 줄에 들어 있는 요소들을 의미한다.
- 파스칼 삼각형의 생성 규칙을 보면, 첫 번째 줄은 항상 숫자 1이고, 두 번째 줄부터 각 숫자들은 자신의 왼쪽 위의 숫자와 오른쪽 위의 숫자의 합으로 구성된다는 것을 알 수 있다.
- 예를 들어, 아래의 3번째 줄의 @2@는왼쪽 위에 있는 2번째 줄의 @1@과 오른쪽 위에 있는 2번째 줄의 @1@의 합으로 이루어진다.

- 이를 수학적으로 표현하면 다음과 같다.
P(3, 2) = P(2, 1) + P(2, 2) = 1 + 1 = 2
*@P(a, b)@ : @a@번째 줄 @b@번째에 있는 값
- 따라서 위의 표현식을 토대로 다음과 같은 점화식을 유도할 수 있다.
$$P(i, j) = P(i - 1, j - 1) + P(i - 1, j)$$
- 이 점화식을 코드로 구현하면 아래와 같다.
- 첫 번째 줄과 두 번째 줄의 경우 @1@로 채워지기 때문에, 반복문을 세 번째 줄부터 진행하도록 해준다. (@range(2, H)@)
- 삼각형의 변에 가까운 부분은 항상 1이므로, 두 번째 값부터 반복문을 진행하도록 해준다. (@range(1, i)@)
for i in range(2, H):
for j in range(1, i):
matrix[i][j] = matrix[i - 1][j - 1] + matrix[i - 1][j]
코드
T = int(input())
for test_case in range(1, 1 + T):
H = int(input())
# 높이가 H이고 1로 채워진 피라미드 모양의 배열을 만든다.
matrix = [[1] * i for i in range(1, H + 1)]
# 알고리즘
# - 맨 위의 숫자는 1
# - 각 숫자들은 자신의 왼쪽 위와 오른쪽 위의 숫자의 합으로 구성된다.
# P(i, j) = P(i - 1, j - 1) + P(i - 1, j)
# 예) P(3, 2) = P(2, 1) + P(2, 2)
# 1 -> [1]
# 1 1 -> [1, 1]
# 1 2 1 -> [1, 2, 1]
# => (3, 2) = (2, 1) + (2, 2) = 1 + 1 = 2
for i in range(2, H):
for j in range(1, i):
matrix[i][j] = matrix[i - 1][j - 1] + matrix[i - 1][j]
print(f"#{test_case}")
for row in matrix:
for item in row:
print(item, end=" ")
print()
참고
- 난이도 : D2
참고 사이트
Pascal's triangle - Wikipedia
From Wikipedia, the free encyclopedia Triangular array of the binomial coefficients in mathematics 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 {\displaystyle {\begin{array}{c}1\\1\quad 1\\1\quad 2\quad 1\\1\quad 3\quad
en.wikipedia.org
'Problem Solving > SWEA' 카테고리의 다른 글
| [SWEA-1974][Python] 스도쿠 검증 (0) | 2023.10.16 |
|---|---|
| [SWEA-1979][Python] 어디에 단어가 들어갈 수 있을까 (1) | 2023.10.14 |
| [SWEA-1983][Python] 조교의 성적 매기기 (0) | 2023.10.12 |
| [SWEA-1989] 초심자의 회문 검사 (1) | 2023.10.12 |
| [SWEA-2001][Python] 파리 퇴치 (0) | 2023.10.12 |
| [SWEA-2007][Python] 패턴 마디의 길이 (0) | 2023.10.11 |
| [SWEA-1859][Python] 백만 장자 프로젝트 (1) | 2023.10.10 |
| [SWEA-2070][Python] 큰 놈, 작은 놈, 같은 놈 (2) | 2023.10.08 |

